尊敬的各位专家、各位同仁: 您们好!我是来自新世纪小学数学成都工作室的陈丹,很荣幸有机会参加本次活动,感谢新世纪小学数学为老师们搭建交流展示的平台。接下来的日子里,我们团队四位老师将在谢定兰老师的带领下一起围绕本次活动主题 “学会学习 —— 发展学生 “量感” 的学习方式” 以五下《长方体的体积》为载体展开探索和研究。 希望在活动中和大家相互交流学习,也希望各位专家和同仁们提出宝贵的意见和建议。谢谢!
【教材图片】https://bbs.xsj21.com/t/1764?p=1#r_73995
【选课思考】https://bbs.xsj21.com/t/1764#r_73999
【教材分析】https://bbs.xsj21.com/t/1764#r_74043
【学情分析】https://bbs.xsj21.com/t/1764#r_74047
【教学目标】https://bbs.xsj21.com/t/1764#r_74049
【教学重点、难点】https://bbs.xsj21.com/t/1764#r_74150
【一稿教学设计】https://bbs.xsj21.com/t/1764#r_74152
【二稿教学设计】https://bbs.xsj21.com/edit/reply/95784
【终稿教学设计】https://bbs.xsj21.com/t/1764#r_97346
尊敬的各位专家、各位同仁: 您们好!我是来自新世纪小学数学成都工作室的陈丹,很荣幸有机会参加本次活动,感谢新世纪小学数学为老师们搭建交流展示的平台。接下来的日子里,我们团队四位老师将在谢定兰老师的带领下一起围绕本次活动主题 “学会学习 —— 发展学生 “量感” 的学习方式” 以五下《长方体的体积》为载体展开探索和研究。 希望在活动中和大家相互交流学习,也希望各位专家和同仁们提出宝贵的意见和建议。谢谢!
【选课思考】 探索体积计算公式是对体积概念的再认识,与长度、面积类似,体积的大小应该用体积单位来度量,但由于很多学生已经知道可以测量长方体的长、宽、高,然后套用公式求体积,所以学生不愿思考长、宽、高这些一维空间的量与用 “体积单位块” 来度量体积之间的关系,甚至混淆长度、面积与体积的单位。因此教学中要重视让学生摆 “体积单位块”,用体积单位块来度量长方体的体积,唤起学生的学习经验,并使他们进一步感受:从长度的认识到面积的认识,再到体积的认识,都是从度量开始研究的。这个过程中既培养学生的量感,又发展学生的空间观念。
【教材分析】 《长方体的体积》是北师大五年级下册第四单元 “长方体(二)” 中的第三课内容。在前两课中学生通过观察、比较、实验等活动已经体会并理解体积和容积的意义,同时又联系生活实际认识了体积、容积单位,在此基础上本课进行了长方体体积计算公式的探索。在探索过程中学生 “得出体积计算公式” 是显性的,感悟 “用体积单位度量” 却是隐性的。
【学情分析】 学生通过第一学段的学习,已经有了长度、面积、角度的度量活动经验,这些活动经验在本课的学习中可以被直接唤醒和运用。通过对学生本课知识的前测,教师发现有部分学生知道 “长方体的体积 = 长 × 宽 × 高 “这个公式,而对于公式背后的数学道理:” 长方体的体积等于其包含的单位体积的个数” 是不了解的,学生需要通过数学活动悟出其中道理。
【教学目标】
1、 结合具体情境和实践活动,探索并掌握长方形等立体图形体积的计算方法,能正确计算长方体等立体图形的体积,解决一些简单的实际问题;
2、在观察、操作、探索的过程中,培养学生动手操作、抽象概况、归纳推理的能力。进一步发展学生的量感。
【教学重点】 经历并理解长方体体积公式的推导过程,掌握的长方体体积的计算方法。
【教学难点】 在同中求异下感受长方体体积计算方法的多样性,在异中求同下感受长方体体积多种计算方法本质的一致性,进一步发展量感。
【教学过程】
一、 直入课题,产生问题(长方体的体积可能与什么有关系?)
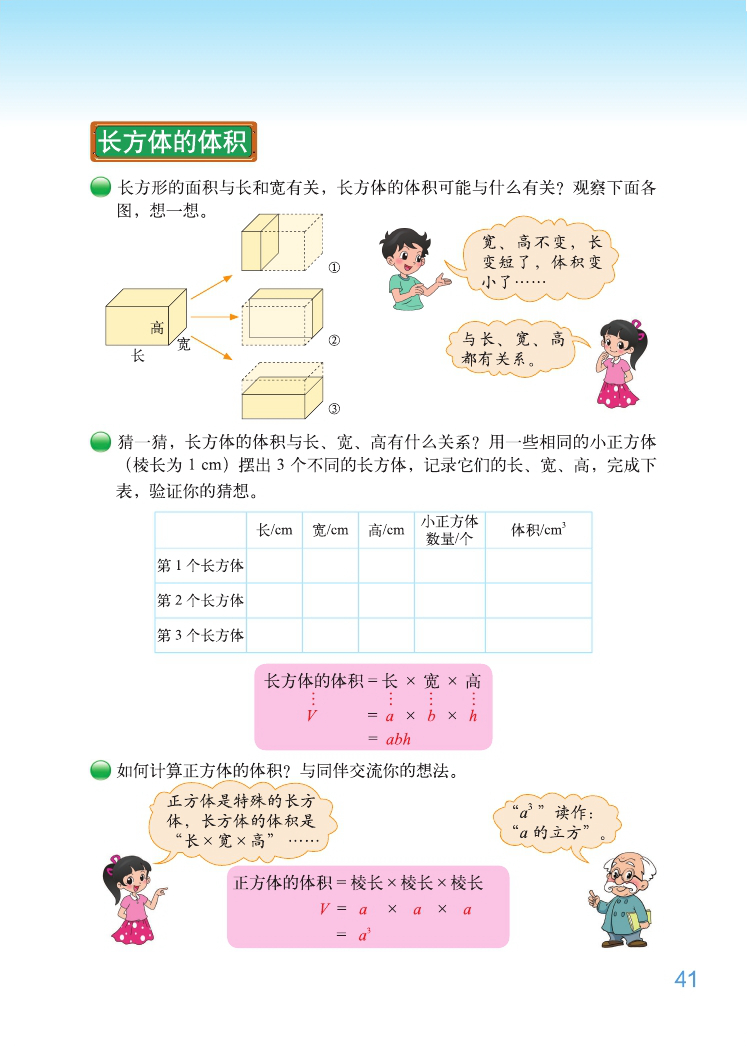
师:一起来读今天要研究的问题。(出示 3 个长宽高各不相同但体积相近的长方体)看到这 3 个长方体,你想提出 什么问题?(3 个长方体谁的体积最大?)你是怎么想的?
师:为什么无法比较?想一想长方体的体积可能和什么有关系?
师:同学们都认为长方体的体积可能和长、宽、高有关系,请你想象一下,当只有长变化的时候,长方体的体积
会怎样变化,你能用手势表示出你的想象过程吗?再看看屏幕上图形的变化与你想象的有什么相同和不同。
ppt 分别演示:
长方体的长延长(宽、高不变),体积变大;
长方体的宽延长(长、高不变),体积变大;
长方体的高延长(长、宽不变),体积变大。
【设计意图】本环节从学生的需求出发层层推动课堂:呈现 3 个长方体,让学生自发产生 “哪个长方体体积最
大” 的疑问,由于无法直观比较出结果而产生第二个疑问:“长方体的体积可能和什么有关系?”。在经历猜
想、想象、验证后,发现长方体的体积与长、宽、高有关,水到渠成进入下一环节的探索,产生第三个疑问:长
方体的体积与长、宽、高到底有什么关系?
二、 鼓励猜想,操作验证(长方体的体积与长、宽、高有什么关系)
师:我们已经知道长方体的体积与长、宽、高但还是无法比较三个长方体的体积怎么办?
师:回顾以前比较面积、长度我们都会找到一个标准来量,体积我们也可以找一个标准来量,我们可以用棱长为 1 厘米的正方体通过测量进行体积的比较。
师:想一想,你打算怎样测量?量一量三个长方体的体积。
学生独立动手操作,集体汇报结果
师:通过测量比较出了三个长方体的体积,你能猜想下长方体的体积和长、宽、高之间有怎样的关系?
师:通过测量三个长方体的体积猜想长方体的体积 = 长 × 宽 × 高?有了猜想我们需要进一步验证。
小组合作摆长方体,用一些相同的小正方体(棱长为 1 厘米)摆出至少 3 个不同的长方体,记录它们的长、宽、
高,完成下表,验证你们的猜想。
1、 四人小组分工明确,确保人人参与活动
2、 小组合作摆长方体,并把有关数据填入下表。
3、 填完后分析数据之间的关系,交流自己的发现。
长 /cm 宽 /cm 高 /cm 小正方体数量 / 个 体积 /cm³第 1 个
第 2 个
第 3 个
第 4 个
第 5 个
小组交流汇报,验证发现:长方体的体积 = 体积单位正方体的个数。
建立每排体积单位正方体的个数、每层体积单位正方体的行数、层数与长方体长、宽、高之间的联系。
得到长方体计算公式。
PPT 回顾分别出示:长方体体积=长 × 宽 × 高
长方体体积=长 × 高 × 宽
长方体体积=宽 × 高 × 长理解写出的每个公式,沟通它们之间的联系,找出它们的不同。
【设计意图】通过量一量、摆一摆的活动让学生经历尝试、猜想、验证的过程。从用 “体积单位块” 量给定的三
个长方体的体积,得到相等的结果,产生猜想:长方体的体积 = 长 × 宽 × 高。再通过全班分小组摆出各不相同的长 方体进行验证,异中求同发现规律。
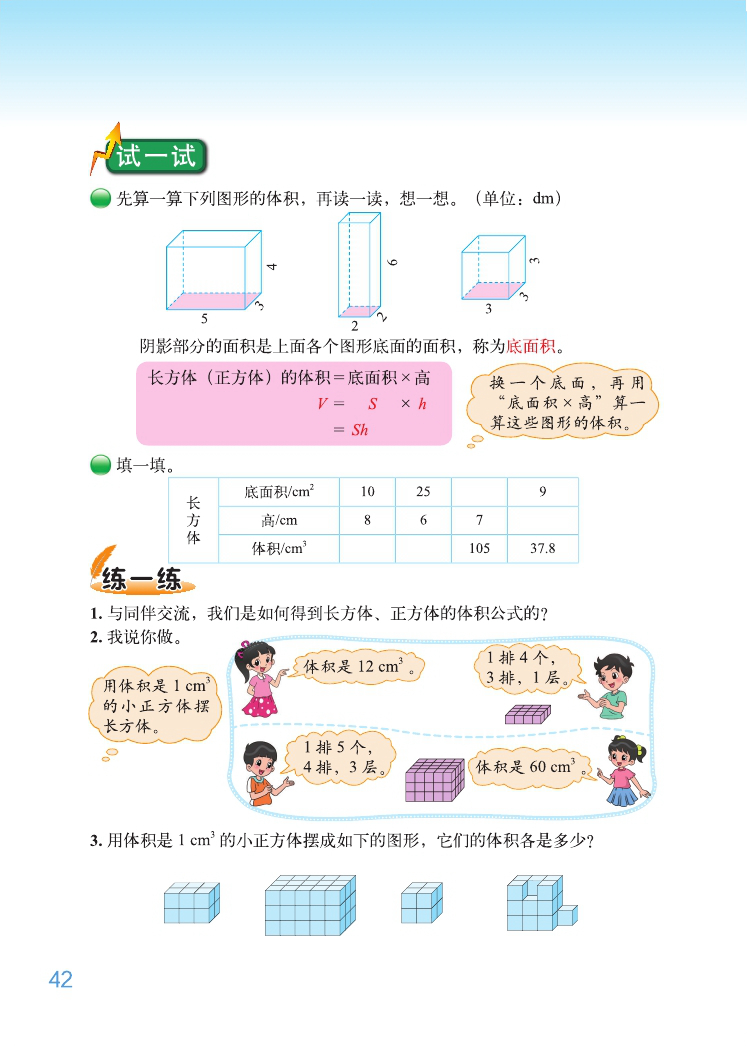
三、引发新思考,叠加量感悟(长方体体积 = 底面积 × 高)
师:通过观察猜想和操作验证,我们已经理解长方体的体积为什么等于长、宽、高三者的乘积。这些不同的方法
中有没有相同之处呢?
长方体的体积=底层所摆的体积单位正方体的个数 × 层数(PPT 将高为 1 厘米的长方体的高从上往下慢慢压缩,至高为 0.5 厘米、0.1 厘米、0.01 厘米......)
长方体的体积=底面所含面积单位正方形的个数 × 高所含的长度单位的个数师:回头来看,我们用单位体积的小正方体测量长方体的体积,明白了长方体体积 = 长 × 宽 × 高里面藏着的道
理。在异中求同又发现长方体体积 = 底面积 × 高。
【设计意图】通过演示发现:原来长方体的体积就等于长宽高三者的乘积,异中求同发现他们都可以用底层所摆
的体积单位正方体的个数 × 层数来表示。然而难点在于学生认为 “面积是平面图形的大小,而平面图形是没有厚
度的,因此是累积不成体的”。通过动画演示让学生展开想象,进行类推:长方体的高逐渐变小,当 “面” 移动
到与底面重合三维就转入二维。继而逆向思考:只要把底面稍微往上移动就能从二维转入三维,从而突破对叠加
量的真正的理解和感悟。
四、类比推测,提出新问题(正方体体积 = 棱长 × 棱长 × 棱长)
师:根据今天的思考大胆的想想你还能解决哪些立体图形的体积?说说你是怎么想的。
正方体体积=棱长 × 棱长 × 棱长
【设计意图】通过前面的探究,有了充分的体验和思考的经验后,将体积计算公式推广到所有柱体体积,发现柱
体体积的共性 “底面所含面积单位的个数 × 高所含的长度单位的个数”。这样不仅为学生后续学习立体图形的体
积搭好了脚手架,更是让每个孩子带着新的思考离开。
五、全课小结。
通过今天的学习,你获得了哪些探索知识的经验和新的方法。
这节课老师直接入课题,提出问题。在教学中老师通过让学生动手操作量一量、摆一摆的活动让学生经历尝试、猜想、验证的过程。从用 “体积单位块” 量给定的三个长方体的体积,得到相等的结果,从而产生猜想:长方体的体积 = 长 × 宽 × 高。再老师又安排全班分小组摆出各不相同的长 方体进行验证,异中求同发现规律。找出长方体的体积计算方法。学生们在动手中感知,在操作中感知。学生在不知不觉中理解了长方体的体积。
陈老师让学生通过动手操作量一量、摆一摆的活动,使学生经历尝试、猜想、验证的过程,感受知识的形成过程,体会数学思想,积累基本数学活动经验。从用 “体积单位块” 量给定的三个长方体的体积,得到相等的结果,从而产生猜想:长方体的体积 = 长 × 宽 × 高。设计合理,凸显了对学生量感的培养。
学生认知是由猜测、动手实践,推导出长方体的体积与长、宽、高的关系时,陈老师注重引导学生通过比较三组长方体体积的大小与长、宽、高有什么关系,通过动手摆不同的四种长方体,记录数据观察得出长方体的体积等于长、宽、高的乘积。最后利用多媒体的演示,突出了重点,分散了难点,使学生既理解了长方体体积的形成过程,又很轻松的掌握了正方体体积的计算。
陈老师在教学中推导公式的过程是让学生先看图猜测长方体的体积与长、宽、高之间的关系,再让学生动手操作摆出四种不同的长方体,通过记录的数据观察交流,归纳出长方体的体积等于长、宽、高的乘积,再次通过课件直观的演示,使学生清楚的归纳出长方体体积的计算公式。
本课巧妙地设计利用学生计算长方形面积的经验设置悬念,这个过程引导学生经历了猜想 —— 迁移 —— 验证 —— 寻求正确的解决问题的方法 —— 拓展的过程 —— 推广应用,充分体现了 “学生是数学学习的主人” 的全新教育理念,全程层层推进,环环相扣,从多角度让学生观察、交流、讨论、练习等形式来培养学生思维表达能力。
本节课的开始,让学生经历 “想象” 一下长方体的体积跟什么有关?这其实是一个在头脑中进行抽象的过程,教师在学生想象过之后,有进行了演示,这对于有些学生不能完成抽象的学生来说,这是非常有必要了,能帮助学生更为直观形象,而对于能抽象完成的学生来说这是一个验证环节。
本节课直接切入主题,提出问题,引发学生思考长方体的体积与什么有关,不拖泥带水,通过演示猜想与长宽高有关。依据猜想进行验证得出结论。整节课老师的教学思路清晰,简单明了,对于高年级的学生比较适合。
注重引导学生通过比较三组长方体体积的大小与长、宽、高有什么关系,通过动手摆不同的四种长方体,记录数据观察得出长方体的体积等于长、宽、高的乘积。最后利用多媒体的演示,突出了重点,分散了难点,使学生既理解了长方体体积的形成过程,又很轻松的掌握了正方体体积的计算。
让学生通过动手操作量一量、摆一摆的活动,使学生经历尝试、猜想、验证的过程,感受知识的形成过程,体会数学思想,积累基本数学活动经验。从用 “体积单位块” 量给定的三个长方体的体积,得到相等的结果,从而产生猜想:长方体的体积 = 长 × 宽 × 高。设计合理,凸显了对学生量感的培养。
陈老师特别注重学生的活动体验,让学生理解公式形成的达程。陈老师通过学生猜一猜、摆一摆的活动让学生经历尝试、猜想、验证的过程,从用 “体积单位块” 量给定的三个长方体的体积,得到相等的结果,从而产生猜想:长方体的体积 = 长 × 宽 × 高。尤其是第三环节更是让我感受颇深,能借助课件演示让学生建立二维与三维间的联系,为 “长方体体积=底面积 × 高” 的公式总结打下基础,在观察分析中培养学生的量感,发展空间观念。
本节课结合具体情境和实践活动,使学生探索并掌握了长方形等立体图形体积的计算方法,能正确计算长方体等立体图形的体积,解决一些简单的实际问题;其次,在观察、操作、探索的过程中,培养学生动手操作、抽象概况、归纳推理的能力,进一步发展学生的量感。
通过试讲我们发现学生的困惑点在于怎样将数 “体积单位块数” 与 “长、宽、高” 之间建立联系,如果从三维的数
个数和一维的量长度联系是学生的困惑点。找准学生学习的困惑点,基于学情,为了让每个孩子都深入思考、学习、 感悟,我们对学生进行前测问卷调查。基于前测结果我们调整了教学设计,第二稿教学设计如下:
【二稿教学设计】
一、 前测引入,引发思考
师: 从前测数据我们可以看出同对于长方体的体积与什么有关?大家都有着不同的猜想,长方体的体积到底和什么有关?一起来看看。
ppt 分别演示:
长方体的长延长(宽、高不变),体积变大;
长方体的宽延长(长、高不变),体积变大;
长方体的高延长(长、宽不变),体积变大。
【设计意图】本环节从学生前测我们发现学生对于长方体的体积除个别同学错误外,其余孩子都能准确地写出长方 体体积计算公式。但对于长方体体积与什么有关?却出现各种不同答案。正因为学生前测猜想,激发孩子们想要验 证。经历课前猜想和想象后、课中自然想要验证。再通过观察来验证猜想:长方体体积与长、宽、高有关,随着
长、宽、高的变化而变化。
二、 鼓励猜想,操作验证(长方体的体积与长、宽、高有怎样的关系)
师:从前测可以看出绝大部分同学都已经知道长方体的体积等于长 × 宽 × 高。一起来看看大家对这个公式的理解。
(出示不同学生对公式的理解并引发冲突,发现都无法解释这个公式的道理。)
师:大家都有着自己的猜想,到底是怎样的需要我们进一步来验证。你们准备怎样来研究?
(通过摆长方体来进行进一步的研究)
小组合作摆长方体,用一些相同的小正方体(棱长为 1 厘米)摆出至少 3 个不同的长方体,记录它们的长、宽、高, 完成下表,验证你们的猜想。
1、 四人小组分工明确,确保人人参与活动
2、 小组合作摆长方体,并把有关数据填入下表。
3、 填完后分析数据之间的关系,交流自己的发现。
长 /cm 宽 /cm 高 /cm 小正方体 数量 / 个 体积 /cm³
第 1 个
第 2 个
第 3 个
第 4 个
第 5 个
小组交流汇报,验证发现:长方体的体积 = 体积单位正方体的个数。理解公式的含义,建立每排体积单位正方体的 个数、每层体积单位正方体的行数、层数与长方体长、宽、高之间的联系。
【设计意图】通过学生前测对长方体体积计算公式理解的不同引发冲突,激发学生想要弄明白长方体的体积为什么 和长、宽、高是相乘的关系。自发想要动手进行验证、猜想。通过全班分小组摆出各不相同的长方体进行验证,通 过操作体验进行演绎推理,不但 “理” 清核心问题,还积累了一定基本活动经验,为后续学习奠定基础。
三、类比推理,正方体的体积计算公式
师:同学们已经理解长方体的体积计算公式。你马上能联想到什么图形呢?
正方体的体积计算公式是怎样的呢?和同桌说说你的想法。
全班交流,类比推理,理解正方体体积计算公式。
【设计意图】通过前面的探究,有了充分的体验和思考的经验后,将长方体体积计算公式类推到特殊的长方体,理 解正方体体积计算公式。培养学生从一般到特殊的合情推理。
四、全课回头看
我们今天是怎么一步一步加深对长方体体积公式的理解的?
再次试讲后我们发现学生的真困惑在于 “明明是数个数,怎么就变成了三条线在相乘” 的困惑中,找准学生的看困难,不仅要让学生明白长方体体积度量的本质,有要理清关系,于是我们又进行了进一步的改动。
一、 前测回顾,发现学生真困惑
师:课前老师两个调查,一起来看看大家的情况。
学生解读自己对长方体体积公式的理解,发现怎么都说不清楚道理。
【设计意图】回顾前测,梳理学生问题和困惑,通过解读前测引发学生思考,感悟本节课学习的必要性。
二、动画演示,验证猜想辨关系
师:长方体的体积到底和什么有关?边看边思考和你之前的猜想一致吗?
ppt 分别演示:
长方体的长延长(宽、高不变),体积变大;
长方体的宽延长(长、高不变),体积变大;
长方体的高延长(长、宽不变),体积变大。
长方体的长宽高都延长,体积变大。
师:通过观察你能来说一说长方体的体积与什么有关?有怎样的关系?
【设计意图】根据学生课前猜想,动画验证猜想。通过观察来验证猜想:长方体体积与长、宽、高有关,随着长、宽、高的变化而变化。同时又产生新的疑问到底有怎样的关系,学生在不断产生新问题中继续学习。
三、 探究明理,把握体积公式度量本质
(一) 明确体积度量本质
师:估一估这个长方体的体积是多少?(实物出示)
师:要知道这个长方体盒子到底有多少怎么办?
师:你准备用什么哪个体积单位来测量?你准备怎么量?
师:能算出体积是多少吗?
师:你们是用什么方法求出长方体体积的?(数个数)
(二)明确长方体体积公式度量本质
师:用数个数的方法是不是就解决了你对长方体体积计算公式的理解?
你们准备怎样进一步研究?
小组合作摆长方体,用一些相同的小正方体(棱长为 1 厘米)摆出至少 3 个不同的长方体,记录它们的长、宽、高,完成下表,验证你们的猜想。
1、 小组合作摆长方体,并把有关数据填入下表。
2、 填完后分析数据之间的关系,交流自己的发现。
长 /cm 宽 /cm 高 /cm 小正方体 数量 / 个 体积 /cm³第 1 个
第 2 个
第 3 个
第 4 个
第 5 个
小组交流汇报,验证发现:长方体的体积 = 体积单位正方体的个数。
理解公式的含义,建立每排体积单位正方体的个数、每层体积单位正方体的行数、层数与长方体长、宽、高之间的联系。
同学们已经明白了长方体体积计算公式?请你来计算这个长方体的体积。
(学生需要数据)知道什么数据就能算?如果只给体积单位块,长度单位你会估吗?
6 表示什么?2 呢?6×2 呢?你怎么知道高是 2 呢?
是不是以后只要遇到要求长方体体积我都用体积单位来摆?那怎么办?
看来长方体的体积计算公式能帮助我们直接就进行计算了,原来它的通用是有道理的。
师:回头来看我们是怎么一步一步加深对长方体体积计算公式的认识的呢?
【设计意图】通过学生前测对长方体体积计算公式理解的不同引发冲突,激发学生想要弄明白长方体的体积为什么和长、宽、高是相乘的关系。自发想要动手进行验证、猜想。通过全班分小组摆出各不相同的长方体进行验证,通过操作体验进行演绎推理,不但 “理” 清核心问题,还积累了一定基本活动经验,为后续学习奠定基础。
三、类比推理,发展度量意识
师:同学们已经理解长方体的体积计算公式。你马上能联想到什么图形呢?
正方体的体积计算公式是怎样的呢?和同桌说说你的想法。
全班交流,类比推理,理解正方体体积计算公式。
【设计意图】通过前面的探究,有了充分的体验和思考的经验后,将长方体体积计算公式类推到特殊的长方体,理解正方体体积计算公式。培养学生从一般到特殊的合情推理。
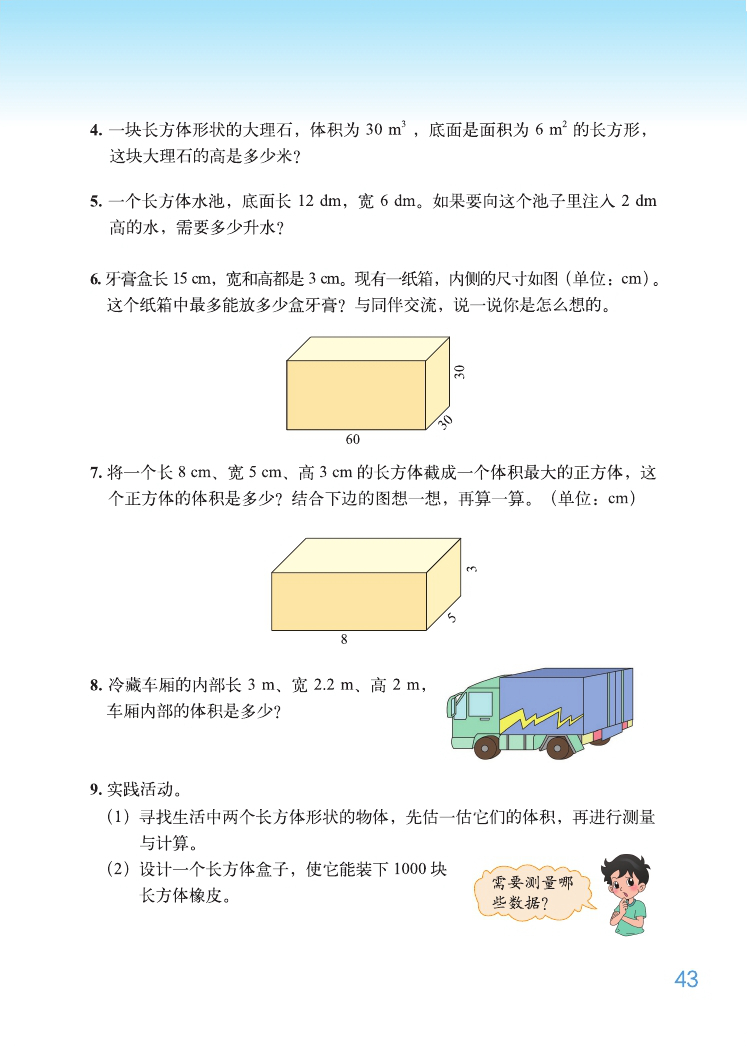
四、 运用公式,练习提升
1、 用棱长为 1 厘米的小正方体摆体积为 6 立方厘米的长方体有几种摆法?
2、 用棱长为 1 厘米的小正方体摆体积为 8 立方厘米的正方体有几种摆法?
通过练习你又有什么新的感悟?运用体积公式能够帮我们找到图形的形状。
【设计意图】学习公式是为了要灵活的运用公式解决问题,让学生在理解体积计算公式的基础上,根据给体积想长度想个数,辨形状。
五、融会贯通,构建空间度量体系。
回顾长度单位、面积单位、体积单位它们测量的道理都是一样的。
现实中,很多学生喜欢直接套用公式求长方体的体积,不愿思考长、宽、高这些一维空间的量与用 “体积单位” 来度量体积之间的关系,甚至混淆长度、面积与体积的单位。重视让学生摆 “体积单位块”,用体积单位块来度量长方体的体积,唤起学生的量感,并使他们进一步感受:从长度的认识到面积的认识,再到体积的认识。这个过程中既培养学生的量感,又发展学生的空间观念。
陈老师在教学中要重视让学生摆 “体积单位块”,用体积单位块来度量长方体的体积,唤起学生的学习经验,并使他们进一步感受:从长度的认识到面积的认识,再到体积的认识,都是从度量开始研究的。这个过程中既培养学生的量感,又发展学生的空间观念。
从学生的需求出发层层推动课堂:呈现 3 个长方体,让学生自发产生 “哪个长方体体积最
大” 的疑问,由于无法直观比较出结果而产生第二个疑问:“长方体的体积可能和什么有关系?”。在经历猜
想、想象、验证后,发现长方体的体积与长、宽、高有关,水到渠成进入下一环节的探索,产生第三个疑问:长
方体的体积与长、宽、高到底有什么关系?
《长方体的体积》这节课隶属于 “图形与几何” 领域,本课是在学生学习了长方体、正方体的特征、表面积的计算以及体积的意义和体积单位之后学习的,纵观本节课学生在观察、操作、讨论、交流、猜测、归纳、分析和整理的探索过程中发展学生的空间观念。