尊敬的各位专家、老师: 大家好!我是成都市杨薪意名师工作室的胡耀老师。非常感谢新世纪小数编委会的各位专家和教育部北京师范大学基础教育课程研究中心数学工作室的各位领导,为广大一线教师搭建展示、交流的平台!感谢您们的指导!感谢工作室领衔人和朋友们的帮助! 在接下来的日子里,我将同小组的彭建华、胡跃庆、李果老师一起,紧紧围绕本次活动的主题 “混合式学习模式实践与探索” 以及数学课程标准、教材、学情等方面分析、思考,设计出本次活动的研讨课例五年级上册《再探 3 的倍数特征》展开本次活动。衷心希望各位专家和同行们提出宝贵的意见和建议,我将认真阅读,思考每一份帖子,不断反思并完善这节课 ! 最后预祝本次大赛圆满成功!祝各位专家、同仁们身体健康!
(第一稿)基于混合式教学理念下选材背后的思考与教材分析:
“3 的倍数特征” 是北师大版教材五年级上册第三单元第 3 课时。在北师大版 3.0 的微课的教学中,老师把着力点放在了 “引导学生掌握 3 的倍数特征,会应用特征判断一个数是不是 3 的倍数” 上。重点让学生经历观察,提出猜想,举例验证,得出结论,并运用结论进行练习和应用。我们发现这样的教学,学生的数学理解仅仅停留于对数学规律的浅层理解,没有达到对数学知识本质的深度理解。
什么是 “3 的倍数的特征” 的数学本质?数学本质是指具体教学内容的本真意义。它既表现为隐藏在客观事物背后的数学知识、数学规律,又表现在为隐藏在数学知识本后的本质属性,又表现为统摄具体数学知识与技能的数学思想与方法。因此,“3 的倍数特征” 这节课的数学本质不仅包含 “各个数位上数字之和是 3 的倍数,这个就是 3 的倍数” 这一规律本身,还应包含 “为什么各个数位上数字之和是 3 的倍数,这个数就是 3 的倍数” 这一规律背后的数学道理及其思想方法,而隐藏在数学规律背后的思想方法蕴含着规律形成过程中丰富的文化特征。
为什么各个数位上数字之和是 3 的倍数,这个数就是 3 的倍数呢?这里面涉及初等数论的问题,涉及整除、同余等内容。任何一个非 0 自然数都可以表示成如下形式:

第一稿教学内容和各个环节设计意图贴:
学习过程:
环节一:复习 3 的倍数特征
师:同学们,昨天我们自学了微课 ——3 的倍数特征。3 的倍数特征是什么?
师:为了检测大家的学习效果,我们玩个小游戏来检测吧。先请偶数列的同学起立,奇数列的同学说一个数,请站着的人判定是不是 3 的倍数,如果回答正确,请他坐下! 如果回答错误,请教教他。比一比:哪一组同桌动作快,开始!
请一组学生上台试一试,重点说清楚你怎么判定的!
反着再来一次!
师:大家有没有发现:玩 3 的倍数特征,简单不?相当于我们玩几年级数学题?
过渡:真厉害!把五年级的知识转化为一年级的数学题,你们还真敢脑洞大开!已经学会了 3 的倍数特征的孩子向老师挥挥手!哇!这么多!我很想知道学习倍数特征这类课时,你有没有一种特别优秀的学习方法分享给大家?
设计目的:通过小环节复习 3 的倍数特征,查看学生是否已经掌握。进行研判是否能进入更深层次的探究与学习。
环节二:复习探究 3 的倍数特征的方法
独学
组学
群学:
猜想(板书:猜想 + 贴)
验证(板书:验证)
结论(板书:结论 + 贴)
过渡:原来先观察,再大胆猜想,最后小心验证,真是数学学习好方法!不过关于 3 的倍数特征,大家真的学会了吗?如果能回答我这个问题,我就相信你们了!
设计目的:通过复习 “观察 —— 猜想 —— 验证” 的一般数学学习方法,再现微课情境,巩固数学方法,也对接下来的探究 3 的倍数特征背后的道理埋下数学方法的伏笔。
环节三:创设情境,发现问题:神秘的 3 的倍数特征。
师:2 秒内判定这个数是否是 3 的倍数。注意:你只有 2 秒的时间。
12、123、99999912、123456789、966952369333。
师:为什么后面的数玩不转了?
师:哈哈,说明 3 的倍数特征我们还没探究到底!否则 2 秒肯定可以判断出来,信吗?那我们今天就再探究 3 的倍数特征。我先考考大家:2、5 的倍数特征看什么位?你们不觉好奇吗?关于 3 的倍数特征,你觉得我们还需要研究什么?
设计意图:通过创设快速判定大数据是否是 3 的倍数,引导学生发现根据 3 的倍数特征 “各个数位数字之和是 3 的倍数” 来判定 3 的倍数,当遇到大数据时,按以往经验费时费力,触发学生的质疑能力,引导学生进入深层次思考,提升思维品质。
环节四:刨根追底,揭示 3 的倍数特征背后的数学道理。
问题:为什么 3 的倍数特征不看个位,而要看所有的数位?
1. 自主探究:以 12、25 为例,我们来研究。请你在学力单探究 1 中。圈一圈,想一想。明确:为什么 3 个一份的圈?
2. 自主探究:以 123 为例,再次验证。
设计说明:再次渗透猜想 —— 验证的数学学习方法,明确 “为什么各个数位上数字之和是 3 的倍数,这个数就是 3 的倍数” 这一规律背后的数学道理及其思想方法,而隐藏在数学规律背后的思想方法蕴含着规律形成过程中丰富的文化特征。
环节五:提升
1. 拓展应用:2、5 的倍数为什么只看个位?
师:探寻 3 的倍数特征,发现 3 的倍数特征本质的研究方法,还能用来干什么?
(1) 回顾开课的练习题
(2) 4 的倍数特征看哪些数位?
(3) 8 的倍数特征看哪些数位?
2. 探寻 2、3、5 的倍数特征。
游戏:学号中大奖,符合条件就起立。
(先猜再动)
(1) 它是 2 的倍数。(2)它也是 3 的倍数。(3)它同时还是 5 的倍数。
师:是几号?
3. 总结第一稿试讲后的反思:【第一次试讲的反思】 (心理状态欠缺)(我还怎么改?)(能否消化杨老师的意见,领悟)(第二次试讲的好评,还欠缺什么?) 通过第一次的试讲,我们整体否定第一稿,因为第一稿的学情是建立在默认学生看完视频后,已经初步掌握 3 的倍数特征,并能简单那运用。面对老师想当然的想法,严重缺乏数学严谨思维,缺乏对学情的真实掌握,课堂变成了 “以师为主” 理想式课堂, 而且整堂课脱离了北师大版 3.0 版本的微课,没有去实现线上线下相结合的混合式教学,所以从学习的效果来看,学生学习是不扎实的、低沉的、被动参与学习的。所以我们看到得是课堂上,只有少部分优秀的学生积极参与课堂里的学习,而其他学生比较安静的看这些学生的 “表演”,没有达成教学目标中 —— 让所有人都掌握为什么 3 的倍数要看所有的数位。 针对以上的试讲问题,我们提出以下整改的方法: (1)重新定位教学目标。 (2)重新去看北师大 3.0 版的微课,找到线上学生学习比较薄弱的环节,寻找适合探究切入点,剪辑视频,重新引入课堂的学习中,使线上线下的混合式教学能够取得真实有效的课堂效果。 (3)删除环节:环节一、二、三 保留环节:环节四:探究 3 的倍数特征背后隐藏的数学道理,并增加计数器模型,总结一个数的倍数特征的背后数学道理,形成探究一个数的倍数特征的基本方法,积累数学经验。
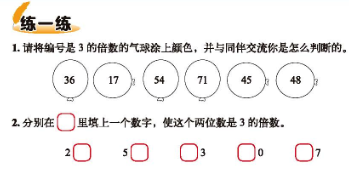
第二稿的教学设计和设计意图: 暖场:游戏:(玩玩 3 的倍数) 规则:轮流报数,遇到该报 3 的倍数和含有数字 3 的数的时候,请喊 “过” 字。 (1)全班玩(2)四人小组玩 设计意图:创设游戏调动孩子的兴趣,让沉默的课堂爆发欢乐,为下一步的学习做好思维铺垫。 正式上课: 环节一:【独立研习,探寻新知】 (环节目标:创设情境,摸底学情,检测 3 的倍数特征学生是否已掌握。) 师:同学们说得真好,那我们带着这些开始上课吧啊! 师:看了微课《3 的倍数特征》的同学们向老师挥挥手,真是一群努力的孩子们!现在老师带领同学们再次回顾微课里的精彩片段吧! 播放视频片段 1:(0 分 26 秒 ¬——0 分 32 秒):我想知道你们现在会怎么找这三个数呢? 预设:学生说出判定 3 的倍数特征的办法。 师:哈哈,看来大家都学会用先进方法了,那我们可以玩游戏了。 小游戏:小考官 师:同学们,你们做过试卷吗?那么你们编过试卷吗?哈哈,我们游戏就是编试卷。 要求:(1)在学力单探究 1:任意编写两个数。20 秒完成 (2)听老师指令,同桌交换试卷完成。 (3)完成批改试卷工作。 群学:选择两组同学上台展示。(一组举手 + 一组不举手) 设计目的:通过教师巡查试卷编制和完成情况,掌握并发现学生存在的问题,比如:数字太多的数怎么快速判定是不是 3 的倍数,用 3 的倍数特征判定方法真的好用吗?了解学生掌握 3 的倍数特征情况后,才能开展 3 的倍数特征背后数学道理的探究。
环节二:【同伴研讨,探究解惑】 (环节目标:通过小组探讨、合作交流,共同探究发现 3 的倍数特征背后的数学道理 —— 每个数位上的余数起着决定作用。) 播放视频,2 分 42 秒 - 3 分 07 秒 ,问:为什么圈起来的数是 3 的倍数? 师:哈哈,说得真好,看来后面的视频老师不用播放了,因为视频后面研究出的结论大家都知道了,那你觉得我们今天再探 3 的倍数特征能再研究点什么呢?(板书:再探 3 的倍数特征) 预设:生提出核心问题:为什么所有数位相加的数字之和是 3 的倍数,这个数就是 3 的倍数?(应对预设的办法:尽量让学生提问,如果这里的学生确实没有探究为什么的习惯,则只能教师提问。)
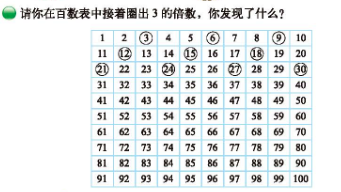
活动一:从两位数开始探究 3 的倍数特征背后的数学道理。 老师从百数表中选出一个数 ——21 活动要求:请你圈一圈、填一填、想一想:为什么 21 的十位数字和个位数字相加的和就是 3 的倍数,这个数 21 就是 3 的倍数? 1. 独学 2. 组学 3. 群学 教师的追问预设: (1)“面对圈 2+1 的情况”,我想问问,这么多圈一圈,你觉得最重要的是哪一个?为什么它最重要?2 表示的是什么意思?1 呢?2+1 表示的是什么?
(2)结合我们的研究问题:“为什么 21 的十位数字和个位数字相加的和就是 3 的倍数,这个数 21 就是 3 的倍数?”;你有什么大胆猜想? 预设:1. 取决于十位和个位的余数。 2. 表面上算十位数字和个位数字的和,实际上算的是十位和个位上余数的和。 小结: 师:也就是判断是不是 3 的倍数,取决于什么?取决于谁的余数?
活动二:探究三位数和多位数是不是 3 的倍数特征的背后数学道理。 第一层次:探究 121 为什么不是 3 的倍数? 师:老师在百位上添一个,这个数(121)还是 3 的倍数吗?为什么? 活动要求:再次以三位数 121 为例验证, 请你在下图中圈一圈,是这样的吗? 想一想:这次怎么圈,可以快速找到分走几个?剩余几个?
第二层次:121 的数位上数字的变化与 3 的倍数关系。 师:最少增加几个可以变成 3 的倍数?如果在百位或十位上添数字,你还可以怎么添加,也能变成 3 的倍数,为什么? 第三层次:引出计数器 —— 小结判定 3 的倍数取决于各个数位上的余数。 师:如果是百位是 3,还需要看百位的余数吗?为什么?这样的情况还有吗? 追问:那到底什么时候可以不看某个数位上的数?引出 33669999663321 这个数是不是 3 的倍数?
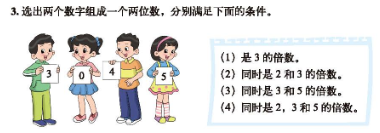
环节三:【团队研述,探索提炼】 (环节目标:通过 3 的倍数特征背后数学道理的探究过程,提炼出 3 的倍数取决于余数的数学经验,这个经验也可以应用于 2、5 的倍数特征,也同样应用于更广泛的倍数特征。) 1. 解释 2、5 的倍数特征为什么看个位? 2. 猜想 4 的倍数特征是什么?那 8 的倍数特征会研究了吗?
板书设计 再探 3 的倍数特征 —— 各个数位数字相加的和是 3 的倍数
猜想 取决于各个数位里的余数
验证 小正方体图 计数器
终稿教学内容和各个环节设计意图:
暖场:游戏:(玩玩 3 的倍数)
规则:轮流报数,遇到该报 3 的倍数和含有数字 3 的数的时候,请喊 “过” 字。
(1)全班玩(2)四人小组玩
设计意图:创设游戏调动孩子的兴趣,让沉默的课堂爆发欢乐,为下一步的学习做好思维铺垫。
正式上课:
环节一:【独立研习,探寻新知】
(环节目标:创设情境,摸底学情,检测 3 的倍数特征学生是否已掌握。)
师:同学们说得真好,那我们带着这些开始上课吧啊!
师:看了微课《3 的倍数特征》的同学们向老师挥挥手,真是一群努力的孩子们!现在老师带领同学们再次回顾微课里的精彩片段吧!
播放视频片段 1:(0 分 26 秒 ¬——0 分 32 秒):我想知道你们现在会怎么找这三个数呢?
预设:学生说出判定 3 的倍数特征的办法。
师:哈哈,看来大家都学会用先进方法了,那我们可以玩游戏了。
小游戏:小考官
师:同学们,你们做过试卷吗?那么你们编过试卷吗?哈哈,我们游戏就是编试卷。
要求:(1)在学力单探究 1:任意编写两个数。20 秒完成
(2)听老师指令,同桌交换试卷完成。
(3)完成批改试卷工作。
群学:选择两组同学上台展示。(一组举手 + 一组不举手)
设计目的:通过教师巡查试卷编制和完成情况,掌握并发现学生存在的问题,比如:数字太多的数怎么快速判定是不是 3 的倍数,用 3 的倍数特征判定方法真的好用吗?了解学生掌握 3 的倍数特征情况后,才能开展 3 的倍数特征背后数学道理的探究。
环节二:【同伴研讨,探究解惑】
(环节目标:通过小组探讨、合作交流,共同探究发现 3 的倍数特征背后的数学道理 —— 每个数位上的余数起着决定作用,经历探究过程,积累探究一个数的倍数特征背后数学道理的数学经验和数学方法。)
师:哈哈,同学们说得真好,看来通过微课的学习,大家已经掌握了 3 的倍数特征,那你觉得我们今天再探 3 的倍数特征能再研究点什么呢?(板书:再探 3 的倍数特征)
预设:生提出核心问题:为什么所有数位相加的数字之和是 3 的倍数,这个数就是 3 的倍数?(应对预设的办法:尽量让学生提问,如果这里的学生确实没有探究为什么的习惯,则只能教师提问。)
活动一:从两位数开始探究 3 的倍数特征背后的数学道理。
老师从百数表中选出一个数 ——21
活动要求:请你圈一圈、填一填、想一想:为什么 21 的十位数字和个位数字相加的和就是 3 的倍数,这个数 21 就是 3 的倍数?
1. 独学
2. 组学
3. 群学
教师的追问预设:
(1)“面对圈 2+1 的情况”,我想问问,这么多圈一圈,你觉得最重要的是哪一个?为什么它最重要?2 表示的是什么意思?1 呢?2+1 表示的是什么?
(2)结合我们的研究问题:“为什么 21 的十位数字和个位数字相加的和就是 3 的倍数,这个数 21 就是 3 的倍数?”;你有什么大胆猜想?
预设:1. 取决于十位和个位的剩余的数。
2. 表面上算十位数字和个位数字的和,实际上算的是十位和个位上剩余的余数和。追问:真的吗?那 51 呢?3 个一圈后,这次十位上的剩余的数字是几?为什么这次剩余的数字不是十位上的数字 5 了?不是和我们的猜想不一样了吗?引导少圈一次,即可达成余数和数位上的数字一样,符合我们的猜想。
小结:师:也就是判断是不是 3 的倍数,取决于什么?取决于谁的余数?
活动二:探究三位数和多位数是不是 3 的倍数特征的背后数学道理。
第一层次:探究 121 为什么不是 3 的倍数?
师:老师在百位上添一个,这个数(121)还是 3 的倍数吗?为什么?
活动要求:再次以三位数 121 为例验证, 请你在下图中圈一圈,是这样的吗?
想一想:这次怎么圈,可以快速找到分走几个?剩余几个?
第二层次:121 的数位上数字的变化与 3 的倍数关系。
师:最少增加几个可以变成 3 的倍数?如果在百位或十位上添数字,你还可以怎么添加,也能变成 3 的倍数,为什么?
第三层次:引出计数器 —— 小结判定 3 的倍数取决于各个数位上的余数。
师:如果是百位是 3,还需要看百位的余数吗?为什么?这样的情况还有吗?
追问:那到底什么时候可以不看某个数位上的数?引出 33669999663321 这个数是不是 3 的倍数?
设计目的:从两位数 21 开始探究,由于 21 这个数的特殊性,通过圈一圈,填一填,想一想,学生可以初步提出猜想:3 的倍数取决于各个数位上剩余的数字;但是也正由于 21 这个数的局限性,容易导致不完全归纳法,给学生造成不严谨的数学研究经验,因此再举例像 51 这类的数,通过少圈一次,也能发现剩余数与数位上原数字一样。再拓展到三位数、多位数,充分利用计数器,验证了 3 的倍数特征取决于各个数位上的剩余的数字,也就是余数。让学生充分经历了 3 的倍数背后数学道理的探究过程,积累了丰富的数学经验和数学方法。
环节三:【团队研述,探索提炼】
(环节目标:通过 3 的倍数特征背后数学道理的探究过程,提炼出 3 的倍数取决于余数的数学经验,这个经验也可以应用于 2、5 的倍数特征,也同样应用于更广泛的倍数特征。)
1. 解释 2、5 的倍数特征为什么看个位?
2. 猜想 4 的倍数特征是什么?那 8 的倍数特征会研究了吗?
设计目的:根据刚才积累的探究 3 的倍数特征背后数学道理的数学经验和数学方法进行拓展和应用,进一步回顾 2、5 的倍数特征,展望 4、8 的倍数特征,形成知识的结构化,走向深度教学。
板书设计
再探 3 的倍数特征
—— 各个数位数字相加的和是 3 的倍数
猜想 取决于各个数位里的余数 验证 小正方体图 计数器
我们在教学中大谈特谈要重视各学科思维(数学思维、语文思维等)的同时,我们是不是意识到我们的教学忽略了课堂中最重要的一点:学生思维。学生在学习中受某个情境、某句话、某个动作、某个图示等所引发的思维流向,他们的所思、所欲、所能、所好,他们想知道什么,由此又想到了什么,切实关心他们的欲望和困惑。
老师对数学本质的挖掘非常深入,先通过 “观察 —— 猜想 —— 验证” ,再现微课情境,最后到圈一圈,逐步引导学生探索 3 的倍数特征背后的道理,很多老师只侧重教 “是什么”,其实真正难的也是非常重要的是 “为什么”,只有让学生知其所以然,才能在应用时以不变应万变。
老师以学生原有认知为基础,激发学生的探究欲望,利用学生刚学完 “2、5 的倍数的特征” 产生的负迁移,直接抛出问题,激活了学生的原有认知,学生自然而然地会将 “2、5 的倍数的特征” 迁移到 “3 的倍数的特征” 的问题中,由此产生认知冲突,萌发疑问,激发强烈的探究欲望,因此学生很快进入问题情境,猜测、否定、反思、观察、讨论,使得大部分学生渐渐进入了探究者的角色。 看一个数是不是 2、5 的倍数,只需看这个数的个位。个位是 0、2、4、6、8 的数就是 2 的倍数,个位是 0、5 的数就是 5 的倍数。而 3 的倍数特征则不然,一个数是不是 3 的倍数,不能只看个位,而要看它所有所有数位上的数的和是不是 3 的倍数。
“再探” 意味着新的认识,更加深刻的认识。本课的设计从 3 的倍数的本质出发,即 “为什么各个数位上数字之和是 3 的倍数,这个数就是 3 的倍数” 的探究,揭示数字背后的规律和本质特征,教学本应 “溯源”,胡老师的这节课很有深度。
三的倍数特征是学生已经归纳出二五倍数的特征,之后进一步用同样的思路进行探索,课中活动通过圈一圈、画一画探索 3 的倍数特征, 通过观察、猜想、验证、归纳,积累数学活动经验,发展了学生的合作、动手、观察、归纳的能力。
@15928820422 正因为我们学校的学生无法直接观察出为什么 3 的倍数特征要看各个数位数字之和,所以需要老师搭建梯子,让孩子经历探究,自己发现,这种成就感是难以描述,是学生最需要的。