尊敬的各位专家、全国各地的老师们:
大家好!我是来自山西省运城市临猗县猗氏镇贵戚坊小学的贾智媛,很荣幸能在新春之际参加第十七届基地教学设计大赛与课堂展示活动。感谢新世纪小学数学教材编委会和北京师范大学基础教育课程研究中心数学课程工作室的各位专家、领导,为我们一线教师搭建展示、交流以及促进专业成长的平台。
我参赛的内容是北师大版 4 年级下册第 5 单元第 4 课时 ——《方程》。未来的日子里,我们陈娇校长、何晓娜主任以及团队中的张勤奋、曹洁、荆茹老师将和我一起,就此课与大家共同探讨。真诚期待全国各地的专家、老师们提出宝贵建议!
最后预祝本次大赛圆满成功!祝各位老师们新年快乐,身体健康,工作顺利!谢谢!
教材图片: https://bbs.xsj21.com/t/2093#r_125080
活动主题解读:https://bbs.xsj21.com/t/2093#r_125265
选课思考: https://bbs.xsj21.com/t/2093#r_125274
学情调研:https://bbs.xsj21.com/t/2093#r_129396
教案一稿:https://bbs.xsj21.com/t/2093#r_125084
一稿反思: https://bbs.xsj21.com/t/2093#r_129395
教案二稿: https://bbs.xsj21.com/t/2093#r_129393
二稿反思: https://bbs.xsj21.com/t/2093#r_140855
教案三稿:https://bbs.xsj21.com/t/2093#r_140680
三稿反思: https://bbs.xsj21.com/t/2093#r_140862
团队磨课图片: https://bbs.xsj21.com/t/2093#r_141232
课后测评:https://bbs.xsj21.com/t/2093#r_141734
教案一稿
《方程》教学设计
【教学内容】
北师大版 4 年级下册第 5 单元第 66——67 页
【教学目标】
1. 结合具体的情境,理解方程的含义,会用方程表示简单情境中的等量关系,在丰富的问题情境中感受生活中存在着的大量的等量关系,体会与生活的密切联系。
2. 在观察、分析、比较、抽象、概括和操作交流中,经历将现实问题抽象成等式与方程的过程,积累将现实问题数学化的活动经验。
3. 使学生获得数学是可以运用他们自己的经验去发现和再创造的积极的情感体验。
【 教学重点 】
理解并掌握方程的意义,能根据已有信息列方程表示具体生活情景中的等量关系。
【教学难点】
会用方程表示事物之间简单的数量关系。
【教学方法】
启发式教学;小组合作交流法、主动探究法、讲练结合法。
【教学用具】
多媒体课件
【教学过程】
一、谈话导入
(出示跷跷板图)
1. 同学们,看,这是什么呢?(跷跷板) ,老师发现同学们都很喜欢玩跷跷板,那要怎样的 2 个人才能玩起来呢?
预设:两个人的体重要差不多。
2. 当两个人的体重差不多时,跷跷板才能保持平衡,也才能玩得尽兴。其实我们有一种仪器,它和跷跷板很相似,你们知道是什么吗?(出示课件:天平)

师介绍:天平是衡量物体质量的仪器。它依据杠杆原理制成,在杠杆的两端各有一小盘,一端放砝码,另一端放要称的物体,杠杆中央装有指针。今天这节课,我们就用天平开启新的知识探索好吗?
【设计意图】从生活中常见的跷跷板出发,从而引出天平,明确天平的原理,激发学生学习数学的乐趣。
二、导入新课
活动一:表示出数量关系
1. 大家猜一猜,如果在天平的左、右托盘中分别放入物品,会出现几种情况?
预设:①左边升,右边降;
②右边升,左边降;
③平衡。
根据学生的回答,教师天平展示,并提问:怎样看出平衡状态?如果天平平衡,说明了什么?
预设:指针指向中间。左、右托盘中的物品质量相等。
课件出示:
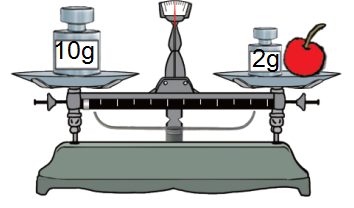
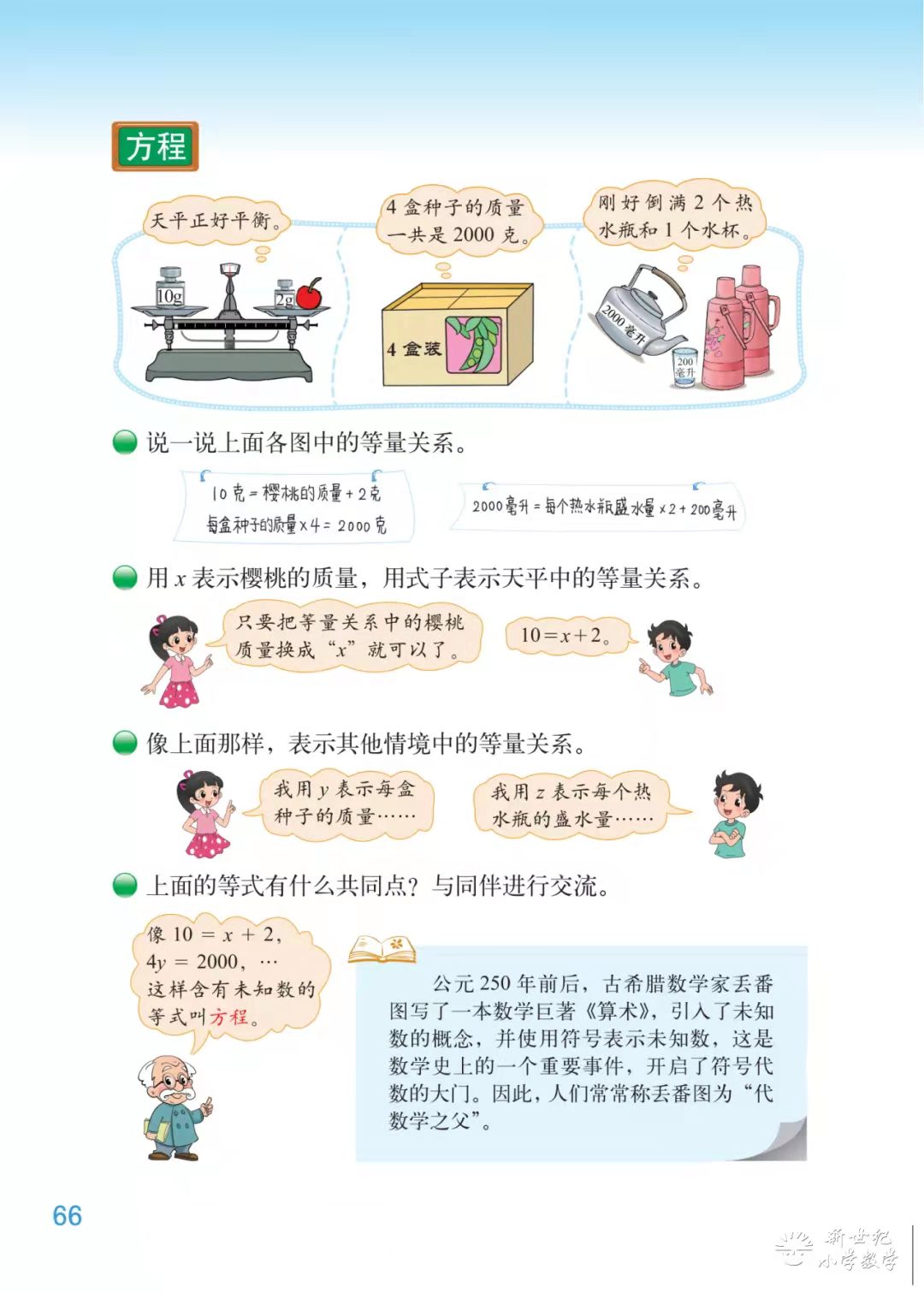
2. 从图中,你发现了什么?
预设 1:天平正好平衡;
预设 2:天平两边的质量相等。
3. 如果用式子表示天平左右两边物体的质量关系,应该怎样表示呢?
预设:10g = 樱桃的质量 + 2g。
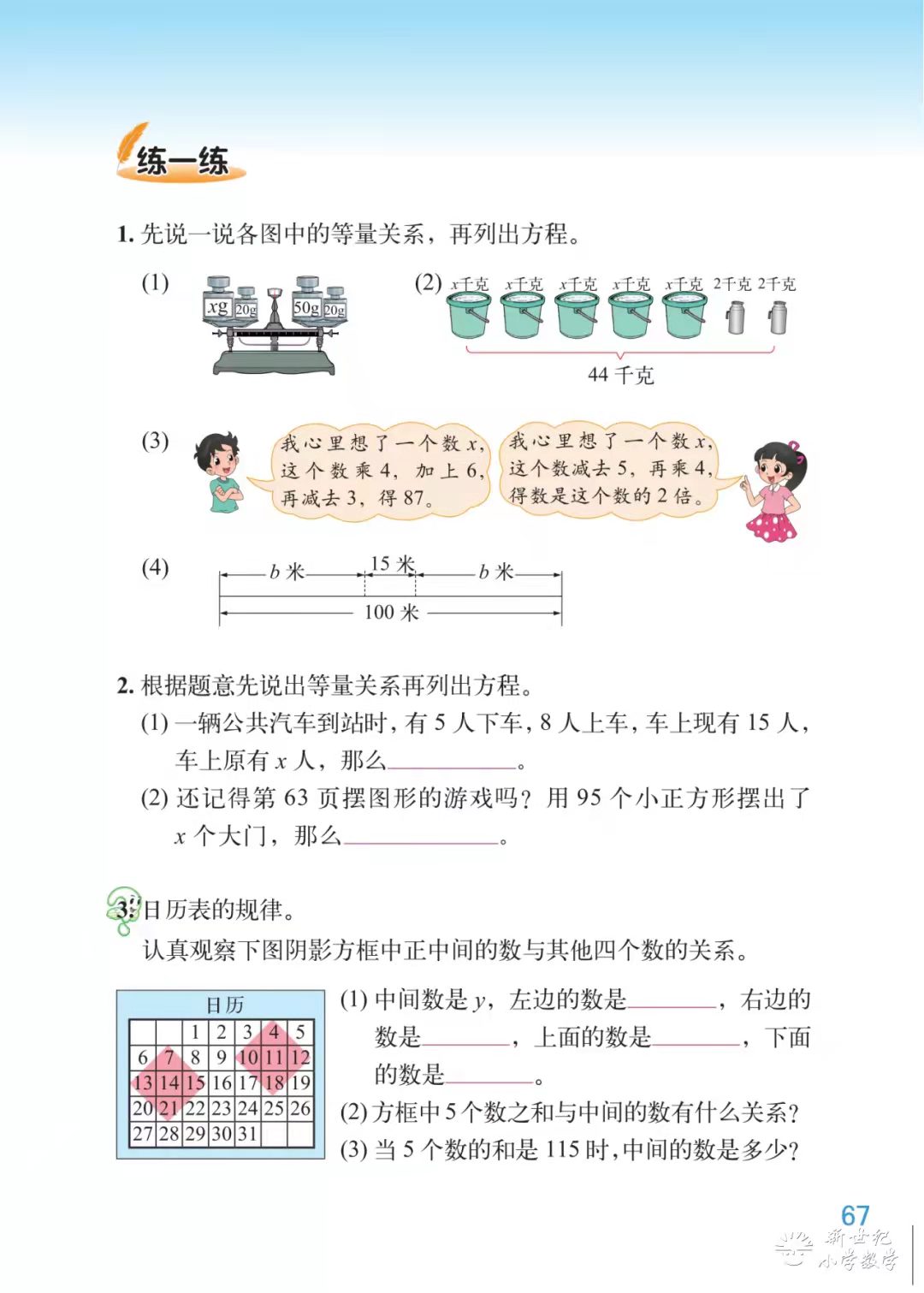
4. 那么你能再说说这两幅图中的等量关系吗?课件出示:
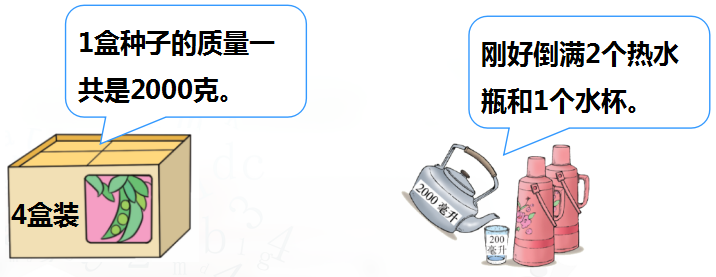
学生独自观察,然后在小组内自由说说。
预设: 每盒种子的质量 ×4=2000g
2000 毫升=每个热水瓶盛水量 ×2+200 毫升
【设计意图】利用看、听、说等活动,让学生感受天平的平衡,进而引出等量关系,符合学生的认知水平。
活动二:用含有字母的式子表示
课件出示:

1. 如果用 x 来表示樱桃的质量,那么你能用式子表示天平中的等量关系吗?并说一说你的想法?
预设:10=x+2。只要把等量关系中的樱桃质量换成 “x” 就可以了。
2. 真是一种不错的方法!那么你能像刚才那样,表示出其他情境中的等量关系吗?
预设 1:我用 y 表示每盒种子的质量,所以是 4y=2000;
预设 2:我用 x 表示每个热水瓶的盛水量,所以是 2000=2x+200。
【设计意图】在探究中感悟、认识,让学生充分经历了知识的产生与发展过程,感受要列出方程找出等量关系是必要条件。
活动三:认识方程。
1. 请观察上述三个等式,它们有什么共同点?在小组内说说。
预设 1:都含有未知数;
预设 2:都是等式。
小结:在数学上,像 10=x+2,4y=2000,… 这样含有未知数的等式叫做方程。这就是我们今天要学习的新知识。
板书课题:方程
2. 大家想想方程必须具备哪几个条件?试着写出几个方程。
3. 其实用未知数表示这样的关系早在公元 250 年前后就出现了。

【设计意图】通过观察认识方程,培养了学生观察、分析、比较、总结、归纳等思维能力。
活动四:方程与等式的区别
1. 看来同学们已经认识了方程,老师也列出了 2 个等式,可是不小心被墨水弄脏了,大家猜猜它原来的式子是不是方程?
课件出示: 7+ ? =95 8x=?
预设 1:第一个等式中如果含有未知数,它就是方程。如果没有含有未知数,那它就不是方程。
预设 2:第二个等式一定是方程,因为它既是等式,又含有未知数。
2、等式和方程有什么关系吗?
小结:所有的方程都是等式,所有的等式不一定是方程。
【设计意图】通过比较方程与等式的区别,加深学生对方程深化理解。
三、巩固练习
1. 用方程表示。
(1)小明的年龄 x 加上 25 岁等于 36 岁。
(2)一个数 x 乘以 5 后,再加上 15 等于 68。
(3)86 减去 6 的 x 倍后是 56。
2. 拓展提高。
三个自然数的和是 63,请根据等量关系列出方程。
3. 布置作业
教材 67 页第 1、2 题。
【设计意图】通过设计不同层次的练习,强化学生对新知的认识与领悟,同时提高学生利用等量关系列出方程的能力。
四、课堂小结
通过本节课的学习,你们有什么收获?
【板书设计】
方 程
10=x+2
4y=2000 含有未知数的等式叫做方程。
2z+200=2000
【设计意图】板书设计简单明了,突出了本节课的重点,深化了学生对方程的理解。
活动主题解读
符号是数学的语言。是人们进行表达、计算、推理、交流和解决问题的工具,学习数学的目的之一是要使学生懂得符号的意义,会运用符号解决实际问题,发展学生的符号意识。英国著名数学家罗素曾说过:“数学就是符号加逻辑。” 可见,数学符号在学习数学中有着举足轻重的地位。在具体情境中培养学生的 “符号意识”,其实就是教给学生在数学王国中巡游的方法。
学生在生活中接触很多用符号来表示的情境,使学生积存了很多潜藏的 “符号意识”,这是培养学生符号意识的重要基础。数学符号的学习过程应遵循从感性到理性运用的辩证过程。因此,教学中教师可以关注学生已有的符号经验,将数学教学设计成看得见、摸得着的物质化实践活动,在解决问题中熟练符号的使用;也要根据学生的认知特点,帮助学生理顺数学概念、规律等符号化的一般关系,从体验到理解运用,再从理解运用到按需要创新来培养学生 “符号思想”,提升符号意识!
选课思考
数学是一个符号化的世界,数学符号就是数学语言,是数学表达、计算、抽象、推理,更是解决问题的重要工具。
数学课程标准指出:“建立符号意识,有助于学生理解符号的使用是数学表达和进行数学思考的重要形式。” 北师大版小学数学四年级下册《方程》一课,引导学生在丰富的具体情境中将等量关系符号化,自然的把现实问题抽象为数学问题,巧妙的把生活世界引向符号世界。
从学习内容角度分析,本课通过引入字母表示现实生活中的未知数,并用等式表示未知数与已知数之间客观存在的等量关系,建立对方程的初步认识;从数学符号的角度分析,方程又是数量符号、运算符号、关系符号等多种数学符号的有效结合。
以本课教材为依托,进行有效的教学,既能有意识的向学生渗透数学符号的数学特质,又能引导学生运用符号化的数学语言描述数学事实。方程,是符号化的简约而条理的数学思考与表达,是对现实问题的准确刻画。学生在认识方程的过程中,自然而然经历了从具体的生活情境抽象出数学符号的过程,运用符号表示数、数量关系,理解符号是数学表达和数学思考的重要形式,发现并深切感受符号的数学价值。孩子们在深度学习的过程中,定会发现符号化的思维优势,爱上符号化的数学语言,有效建立符号意识。
教案二稿
《方程》教学设计二稿
【教学内容】
新世纪小学数学四年级下册第五单元《方程》66-67 页。
【教材分析】
为了使学生体会方程是刻画现实世界的一个有效的数学模型,产生学习方程的欲望,教材设置了多方面的问题情境,第一个问题是用口头语言描述具体情境中的等量关系;第二个问题与第三个问题是引入字母表示未知数,并用式子表示情境中的等量关系;第四个问题是观察上述表示等量关系的式子,抽象概括它们的共同特征,认识方程。教材非常重视对相等数量关系的挖掘和描述,为后面列方程解决实际问题打下了良好的基础。
【教学目标】
1. 结合具体情境了解方程的意义,会用方程表示简单情境中的等量关系。
2. 经历将现实问题抽象成等式与方程的过程,积累将等量关系符号化的活动经验。
3. 在丰富的问题情境中感受生活中存在大量的等量关系,体验数学与生活的密切联系。
重点:理解并掌握方程的意义,能根据已有信息列方程表示具体生活情景中的等量关系。
难点:会用方程表示事物之间简单的数量关系。
【教学用具】
多媒体课件
【教学过程】
一、 链接旧知,激活符号经验
同学们,这节课老师给大家带来了三幅图,你能说一说图中的等量关系吗?
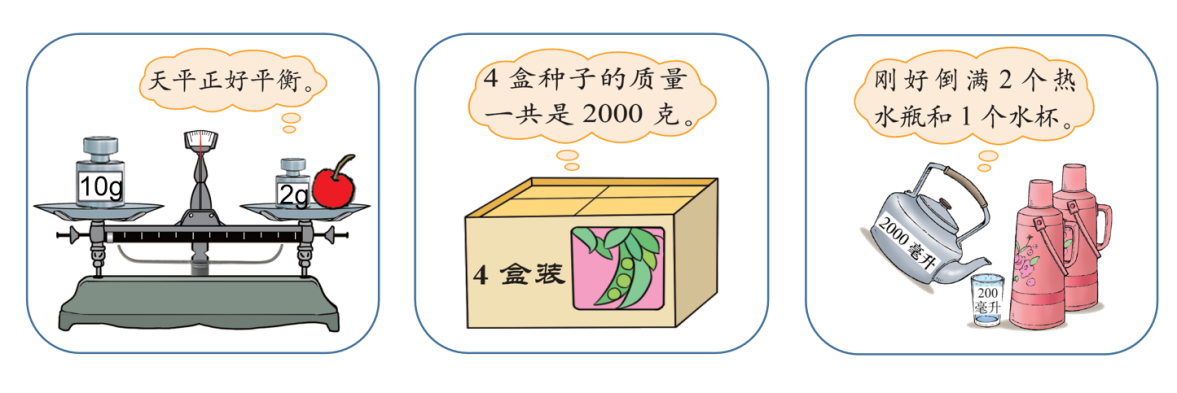
第一幅图:
预设:10 克 = 一个樱桃的质量 + 2 克。
第二幅图:
预设 1:4 盒种子的质量 = 2000 克。
预设 2:说得还不够具体。每盒种子的质量 ×4=2000 克。
第三幅图:
预设 1:2000 毫升 = 每个热水瓶的盛水量 ×2 + 一个水杯的盛水量。
预设 2:从图中我们还可以知道一个水杯的盛水量是 200 毫升,所以这幅图的等量关系还可以写成:2000 毫升 = 每个热水瓶的盛水量 ×2+200 毫升。
【 设计意图 】本节课是在学生学习了用字母表示数和等量关系的基础上进行教学的,所以找出等量关系是列出方程的关键,因此通过此环节为后面列出方程做足了准备。
二、 实践体验,发展符号意识
活动一:观察情境图,寻找等量关系
1. 以第一幅图为例,请写出你认为最简洁的表示方式。
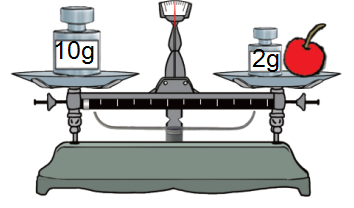
预设:10= +2,10=?+2,10=()+2,10=O+2,10= +2,10=a+2,10=x+2。
2. 谁还有不同的方法来表示樱桃的质量?
3. 总之,大家都是用一个符号表示出了樱桃的质量,真了不起!你们和数学家韦达想的一样。不过另一位数学家笛卡尔说大家的符号各不相同,太乱了。所以他提出统一用字母表中后几个字母 x、y、z 来表示,而且这种方法沿用至今。
4. 大家看,哪位同学就用的是其中的字母之一。我们把他的方法记录在这里。板书(10=x+2)
【 设计意图 】数学符号的引入,可以简短地表示和反映数量关系,所以让学生经历 “从具体事物到
学生个性化的符号表示到学会数学地表示” 这一逐步符号化的过程,感受引入符号的必要性,理解数学符号的作用和价值。
活动二:用含字母的式子表示等量关系
1. 你能借鉴笛卡尔的方法,表示后两幅图中的等量关系吗?
预设:4y=2000, 2z+200=2000,
2. 你为什么这么表示?你是怎么想的?
【 设计意图 】通过让 学生体会使用习惯化的符号表示数量关系的优越性,感悟符号的使用是数学表达和进行数学思考的重要形式,充分激发学生的符号意识。
活动三:归纳总结,认识方程
1. 仔细观察上面的算式,有什么共同点?
预设 1:都有等号。
预设 2:都含有字母。
小结:含有未知数的等式叫做方程。
2. 播放视频:方程的起源。
【设计意图】 通过比较归纳,引导学生把握方程的特点 -- 含有未知数的等式,并让学生了解方程的产生与发展过程以及数学与人类文明进步的联系,凸显数学的文化特征。
三、 综合应用,巩固提升符号意识
1. 先说一说各图中的等量关系,再列出方程。
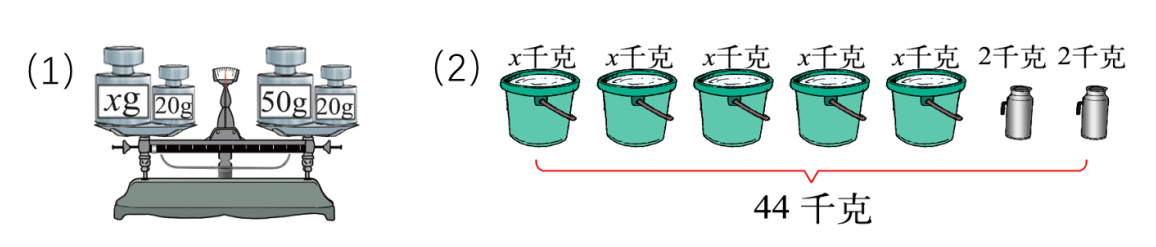
(3)

2. 看图列方程。
(1)长方形的面积 = 72 平方米。
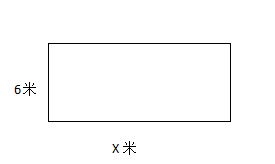
(2)长方形的周长 = 36 米。
3. 淘气写了一个方程:2x+3=17。请你帮淘气写出一个符合这个方程的实际问题。
【设计意图】在丰富的问题情境中,积累将等量关系符号化的活动经验,并与课前测评完美对接,逐步深化学生的符号意识。
四、联系生活,激发符号意识
生活是数学的源泉。在现实生活中,各种各样的符号处处可见。大街、小巷、剧院、会场、家庭、学校、医院…… 只要学生生活过的地方,都能随处见到各式各样的符号。招牌上的 “m”,表示麦当劳;公共场所的 ,表示禁止吸烟;某场所有标志 “P”,表示可以停车场等等。
【设计意图】语言学家皮埃尔・吉罗说:“我们是生活在符号之间。” 通过学生已有的生活经验,让他们初步感受到符号存在的现实意义以及生活中的符号所体现出的简约的特质,而这种符号意识对数学符号感的形成也起着积极的促进作用。
五、板书设计
方程
10=x+2
4y=2000 含有未知数的等式叫做方程。
2z+200=2000
一稿反思
本课是学生第一次认识方程,也是学生由算术思维迈向代数思维的新起点,更是发展学生符号意识的关键一课。
第一次试讲后,不足之处如下:
1. 导入部分,在上一节《等量关系》一课中学生已经具备根据天平的平衡状态、以及其他生活情境列出相应等量关系的学习经验,而本次教学设计中,导入冗长而单一,过分依赖天平情境,无法有效抓住学生注意力。
2. 学生尝试用式子来表示等量关系时,教师直接给出了用 x 来表示未知的量,学生无法体会用字母表示未知量的来源和必要性,不够开放,同时也限制了学生的创新性思维和符号意识的培养。
3. 学生只是表面上理解了方程的特征,但对学习方程的意义仍然有所欠缺。
4. 教学过程中,教师的语言要进一步润色,使得课堂更加连贯、畅通。
学情调研及分析
《方程》这节课是在学生已初步积累一定的活动经验,认识了用字母表示数和等量关系的基础上进行教学的。列方程的依据是等量关系,所列的方程和所写的等量关系必须是相对应的,如何引导学生分析提炼数学问题中的等量关系,建立方程模型,将学生的数学世界由生活化向符号化的转化,最终为形成方程思想打好基础呢?为此,我们进行了一些思考与尝试,对四年级 6 个班 380 位学生进行了教学前测,以便更准确的定位教学起点。
【前测内容】
1. 请用你认为最简洁的方式,表示下面各图中的等量关系。
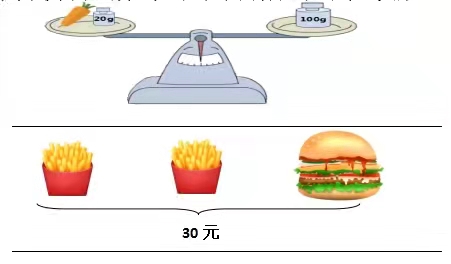
2. 你知道什么是方程吗?用自己的语言说一说,或者写出你知道的方程。
3. 联系生活,想一想:“x+2=10” 可以用来表示什么?(请画一画、或者写一写,把自己的想法表示出来。)
【数据整理】
前测人数:380 人
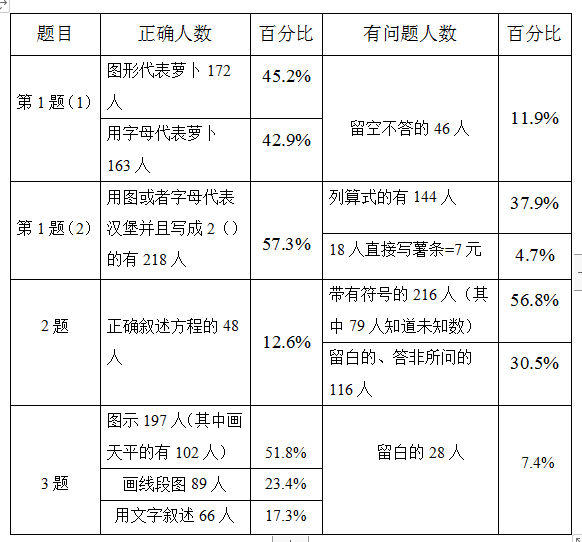
【数据分析及思考】
根据上述数据,反应了学生符号意识的发展及发散性思维的形成过程,这就需要我们在教学中先引导学生表示图中的等量关系,力求多种表示方法,再用简洁的方式来表示自己书写的等量关系,让他们的思维逐步深入发展,探究就会更有意义。
脱离问题情境,知道并能从外在形式化的角度正确识别方程的学生占到四成多,那么我们在设计教学过程中,加入古人对方程的界定,并设计有趣的探究活动让学生逐步对方程有所了解,最后深入理解方程的概念。
对于方程 “x+2=10” 所表示的意义,学生虽然没有积累太多运用天平的经验,但都很自然地与天平取得了联系,体现了类似天平左右两边相等的现象。也就是说对等式有一定了解,这里我们在教学中可以加入不等式,对比研究,进一步让学生体会方程的意义。
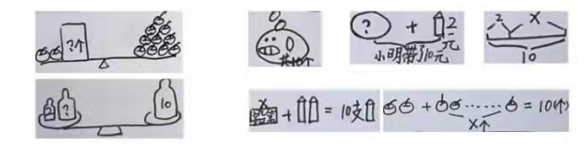
可以说,直观、形象、易操作的天平在学生的头脑中存在具体的表象。通过天平,方程变得不再遥远和神秘,甚至可以成为他们心中方程的代名词。
数学符号的引入,可以简短地表示和反映数量关系,所以让学生经历 “从具体事物 学生个性化的符号表示 学会数学地表示” 这一逐步符号化的过程,感受引入符号的必要性,理解数学符号的作用和价值。
仔细观看了贾老师的两次教案设计,每一次的教案设计都是建立在学生的认知基础上,通过激发学习兴趣,建立学生的符号意识,另外能关注课堂上学生的参与度及思维提高,注重了知识的拓展,关注学生综合能力的提升! 两次的设计,我更看好第二次的教案设计,更开放、更有深度和高度,让学生的思维和认识都有所提高和拓展,让学生在循序渐进中明白了方程的意义及组成,让学生对符号有了内化的认识,把平时用语音表达的情况,用方程更简洁明了的表示出来! 后面提高练习里,让学生说淘气写的方程能解决什么实际问题,是否可以设计让学生小组一起,自己写出一个方程,让组员编写能解决什么问题,或者,组长写一个方程,其他组员都给方程来说能解决哪些实际问题,这样一方面自己写的方程考同学,兴趣浓厚,另一方面体会到同一个方程可以解决很多不同的生活实际问题,体会到数学知识与生活的联系。
贾老师的课充分的体现了新课程改革的思想,教学过程中,让学生体会到了方程是一种数学模型,通过让学生观察天平的相等关系,感受方程与日常生活的联系,体会方程用数学符号抽象地表达了数量关系,加深了对方程意义本质的理解。
强调问题中的基本数量关系,既把握通则通法,又鼓励思维的灵活多样。在概念建立后,让所有学生都掌握编写方程的要点,体现了人人都能获得必须的数学,让不同学生自主编方程,体现了不同人学习数学的不同感悟。
贾老师直奔主题,让学生谈一谈对方程有什么问题,实际实在摸底学生的实际知识水平,接着展示天平,然后提问:谁能说一说这两种东西的质量关系?这样的教学设计不仅联系了生活实际,较好的激发学生学习兴趣。更重要的是使学生从自由放东西的过程中较自主的体会到等式的特征 (左右两边相等)。
教案三稿:
《方程》教学设计三稿
【教学内容】
新世纪小学数学四年级下册第五单元《方程》66-67 页。
【教材分析】
本课是学生第一次认识方程,也是学生由算术思维迈向代数思维的新起点。无论用字母表示数,还是寻找数量间的等量关系,对于四年级学生而言都是很抽象的。同时,本单元内容又是后面学习代数相关知识的基础,所以这部分的教学至关重要。为了使学生体会方程是刻画现实世界的一个有效的数学模型,产生学习方程的欲望,教材设置了多方面的问题情境,第一个问题是用口头语言描述具体情境中的等量关系;第二个问题与第三个问题是引入字母表示未知数,并用式子表示情境中的等量关系;第四个问题是观察上述表示等量关系的式子,抽象概括它们的共同特征,认识方程。教材非常重视对相等数量关系的挖掘和描述,为后面列方程解决实际问题打下了良好的基础。
【教学目标】
1. 结合具体情境了解方程的意义,会用方程表示简单情境中的等量关系。
2. 经历将现实问题抽象成等式与方程的过程,积累将等量关系符号化的活动经验。
3. 在丰富的问题情境中感受生活中存在大量的等量关系,体验数学与生活的密切联系。
重点:理解并掌握方程的意义,能根据已有信息列方程表示具体生活情景中的等量关系。
难点:会用方程表示事物之间简单的数量关系。
【教学用具】
多媒体课件
【教学过程】
一、链接旧知,激活符号经验
今天老师请来了一位数学家,瞧!他从古希腊走来,认识他吗?他就是古希腊的数学家 — 丢番图,被人们称为 “代数学之父”。丢番图喜欢用符号表示未知数,开启了符号代数的大门。这节课我们就跟随他的脚步走进神奇的符号世界!
请看这三幅图,你能说一说图中的等量关系吗?
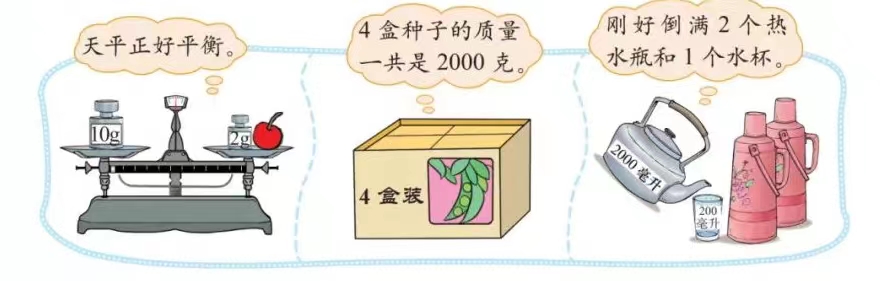
第一幅图:
预设 1:10 克 = 一个樱桃的质量 + 2 克。
预设 2:10g-2g = 樱桃的质量。
第二幅图:
预设 1:4 盒种子的质量 = 2000 克。
预设 2:每盒种子的质量 ×4=2000 克。
第三幅图:
预设 1:2000 毫升 = 每个热水瓶的盛水量 ×2 + 一个水杯的盛水量。
预设 2:从图中我们还可以知道一个水杯的盛水量是 200 毫升,所以这幅图的等量关系还可以写成:2000 毫升 = 每个热水瓶的盛水量 ×2+200 毫升。
【 设计意图: 关于 “符号思想” 的理论,最早可追溯至古希腊数学家丢番图,将 “符号表示未知数” 的研究置身于漫长的 “数学史” 中,激发学生探究的欲望。同时本环节在学生已有的 “用字母表示数” 和 “等量关系” 的基础上进行教学,为后面认识方程做足了准备。】
二、实践体验,发展符号意识
活动一、用简洁的方式表示等量关系
1. 大家都成功找出了三幅图中的等量关系,但数学讲究简洁美,你能把这些长长的等量关系式用最简洁、最简短的的方式表示出来吗?以第一幅图为例,快试试吧。
预设:
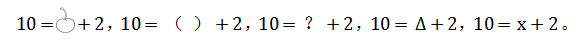
2. 谁还有不同的方法来表示樱桃的质量?
3. 刚才大家都是用一个符号表示出了樱桃的质量,这个想法和数学家韦达想的一样,真了不起!不过另一位数学家笛卡尔却觉得我们的符号各不相同,不便于研究。他提出用字母表中后几个字母 x、y、z 统一来表示,而且这种方法沿用至今。板书(10=x+2)
【 设计意图: 数学符号的引入,可以简短地表示和反映数量关系,所以让学生经历 “从具体事物 学生个性化的符号表示 学会数学地表示” 这一逐步符号化的过程,感受引入符号的必要性,理解数学符号的作用和价值。】
活动二:用含字母的式子表示等量关系
你能借鉴他的方法,表示后两幅图中的等量关系吗?
预设:4y=2000, 2z+200=2000。
【 设计意图: 通过让 学生体会使用习惯化的符号表示数量关系的优越性,感悟符号的使用是数学表达和进行数学思考的重要形式,充分激发学生的符号意识。】
活动三:归纳总结,认识方程
仔细观察上面的算式,有什么共同点?
预设 1:都有等号。
预设 2:都含有字母。
小结:含有未知数的等式叫方程。
追问:判断一个式子是否是方程,需要具备哪些条件?
【设计意图: 在经历了简洁的数学式子表达后,让学生在合作中思考,在思考中辨析,在辨析中寻找方程的关键特征 ——“含有未知数” 与 “等式”,从而理解方程意义中最重要的内涵。】
活动四:串联旧知,感受方程思想
1. 从一年级开始方程就藏在我们身边了。
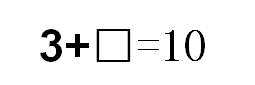
2. 二年级时我们也学过方程。你能找到等量关系,并列出方程吗?
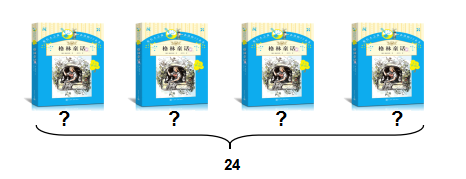
3. 三年级也接触过方程,你能用方程表示下列图中的等量关系吗?
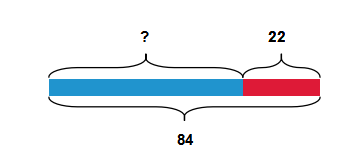
4. 而到了四年级,通过字母表示数和等量关系帮助我们认识了方程,而方程以后也会帮助我们更好的解决问题。
【 设计意图: 在学生认识了方程的形式特征的基础上,让学生重回起点,站在新的高度进行新的思考,将方程的教学置于由易到难、螺旋上升的整体性知识系统中,强调方程就是在已知与未知之间建立等量关系,凸显方程的建模本质。】
三、综合应用,巩固提升符号意识
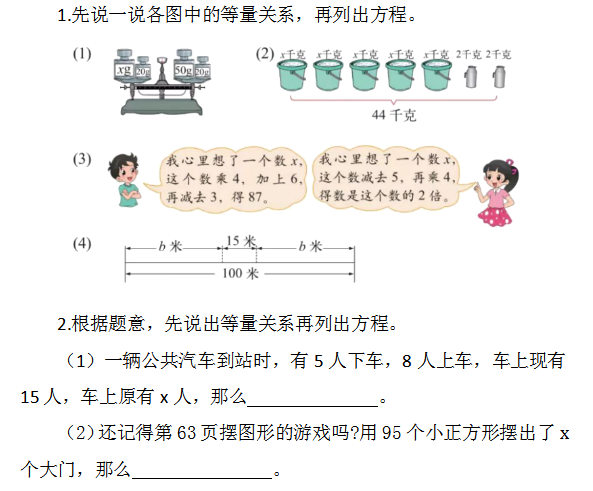
【 设计意图: 这些练习题的设计,从本质上也是帮助学生理解方程的意义,也就是利用等量关系构造方程模型,让学生经历以 “问题情境 ——— 已知数、未知数、等量关系 ——— 建立方程(模型)” 的数学活动过程,不断丰富 “方程表示已知数与未知数之间的等量关系” 的涵义,感悟模型思想的本质,积累数学活动经验,这样的教学设计更有利于学生去发现、提出、分析、解决问题,培养创新意识。】
四、板书设计
方程
10=x+2
4y=2000 含有未知数的等式叫做方程。
2z+200=2000
二稿反思:
在一稿反思的基础上,我们对教学设计作了相应的修改,主要包括:
1、去掉了一稿中利用天平情境的导入环节。由于上节课学生已经学习了等量关系的内容,有了一定的知识基础,而等量关系又是方程的核心,所以我们通过让学生找出三幅图中的等量关系入手,为后面学习方程做好准备。
2、针对教师直接给出用 x 来表示未知的量,学生无法体会用字母表示的来源和必要性。二稿我们将教学设计修改为 “用你认为最简洁的方式表示等量关系。” 使学生经历从具体事物→学生个性化的符号表示→学会数学地表示这一过程,理解数学符号的作用和价值。并避免使学生认为 “含有字母的等式就是方程”。
不足之处:
1、教学设计第四部分:联系生活,激发符号意识,在这一环节向学生介绍生活中的符号,本意是进一步渗透符号思想,我们研讨后觉得这个环节与本节课没有实质性的联系,建议删除这部分内容。
2、课堂上数学用语不够规范,比如:在对 10=( )+2 进行描述时,没有引导学生的数学用语,“我用( )表示樱桃的质量,我列出的式子是( )”,如果这样规范引导,那学生的数学语言表达也会更加规范。
3、课堂练习环节,我设计了这个练习 “淘气写了一个方程:2x+3=17。请你帮淘气写出一个符合这个方程的实际问题。” 本意是想拓展延伸,让学生感受符号在现实生活中的应用,但是从学生的课堂表现看,这样设计问题,很大程度上限制了学生的思维,问题的设计不是很理想。
有碰撞才有火花,在我们团队一次次的思维碰撞中,进一步感受到了 “纸上得来终觉浅,绝知此事要躬行” 的道理,在 “有过程” 的教学中,形成对符号的认识,渗透建模思想。
三稿反思:
失之东隅,收之桑榆。
又一场疫情接踵而至,我们居家学习,减缓了课堂研究的进程。复学第二天,我们团队再次研讨,对教学流程进行了调整,并进行又一次的试讲,结果有惊喜也有不足。
首先,孩子们对于 “10 克 = 1 个樱桃的质量 + 2 克” 的简洁书写和语言表达令人惊喜,在这个过程中,孩子们尝试运用简笔画、图形、常见的括号、字母等等表示樱桃的质量,和上一次的课堂相比,孩子们有了更多的创造,而且,在多种表示方法的对比中,孩子们更能体会到 “可以借助符号” 来表示现实情境中的数学问题。另外,在语言表达方面,孩子们也学会了梳理知识脉络,语言表达条理清晰。
其次,三稿的教学增加了知识串联环节,在学生认识了方程的形式特征的基础上,比如:在一年级算式 3+□=10,二年级的实物情境图,三年级的线段图中,引导学生重回起点,站在新的高度进行新的思考,将方程的教学置于由易到难、螺旋上升的整体性知识系统中,强调方程就是在已知与未知之间建立等量关系,凸显方程的建模本质。
教学是门有遗憾的艺术,反复研讨、反复交流是逐步走向完善的良方。在我们对这稿教学设计的研讨交流中,争议最多的有三个问题:
一是课堂导入环节,把数学史前置,我们的意图是将 “符号表示未知数” 的研究置身于漫长的 “数学史” 中,激发学生探究的欲望,为后面认识方程做足准备。这样调整之后,学生对丢番图很陌生,对他的研究也提不起兴趣,所以这样一开课,就导致部分学生缺乏激情,影响课堂效果。
二是课堂练习环节,练习缺乏层次性,只是单纯巩固了学生的知识能力,对学生的数学思维和建模思想并没有得到更好的提升。课堂练习的设计还需再斟酌,增加拓展性的练习,进一步发展学生数学思维,增加对 X、Y、Z 等数学符号的认识,并能赋予现实的生活情境和意义,积累数学活动经验。
三是教师的数学语言要严谨,规范课堂提问。如果说问题是思维的向导,课堂提问就是教学活动的催化剂。因此,在了解学生学情和对符号意识的理解的基础上,做好课堂预设,精心设计课堂问题,并做好追问,唤醒学生已有经验并展开联想。
在一次又一次的交流中,孩子们有不同的课堂生成,团队成员也有不同的思维碰撞,正是这一次次的碰撞,让我对 “方程”、对 “符号” 都有了更加澄澈的理解。
团队磨课图片:
带着对对 “符号意识” 的初步研究,对教材的粗浅理解,对学情的综合把握,我们的第一次试讲开始了。
第一次试讲的课堂上,有惊喜,也有疑惑。孩子们在课堂上的学习、思考、表达,启发了我们团队对《方程》这一课、“符号意识” 培养、学生综合素养提升等方面,更多的疑问和思考。
第一次研讨:我们重新审视学生的 “符号意识” 基础,思考学生学习 “方程” 的价值和意义,认识到课堂前测的重要性,体会将学生的生活经验和数学活动经验有机统一、螺旋上升培养 “符号意识” 的必要性。




第二次试讲:基于第一次试讲中暴露的问题与可取之处,我们团队做了有关课堂前测,对课堂教学环节做出了调整,对问题的设计进行了仔细的推敲,给了孩子们更多展示和表达的机会,学生在探究过程中,进一步积累了使用 “符号” 进行思考和表达的活动经验。
第二次研讨:“纸上得来终觉浅,绝知此时要躬行”。我们基于 “课堂教学” 主阵地,查阅大量关于 “符号意识” 以及 “学生核心素养” 的有关资料,在 “有过程” 的教学中,培养 “符号意识”,建立模型思想。



第三次听课:在课前所做的学情分析、教育局领导的有效指导、团队成员的奋力研讨中,我们的课堂也在逐步改进。以教学活动为支撑,孩子们有了更多思考和探究的时间和空间,“符号意识” 的觉醒和诠释着实令人惊喜。
第三次研讨:众人拾柴火焰高。我校全体数学教师共同探讨,研究如何让学生理解符号的内涵与实际意义,积累使用符号的活动经验,理解符号的使用是数学表达和进行数学思考的重要形式,培养学生符号意识。





课后测评:
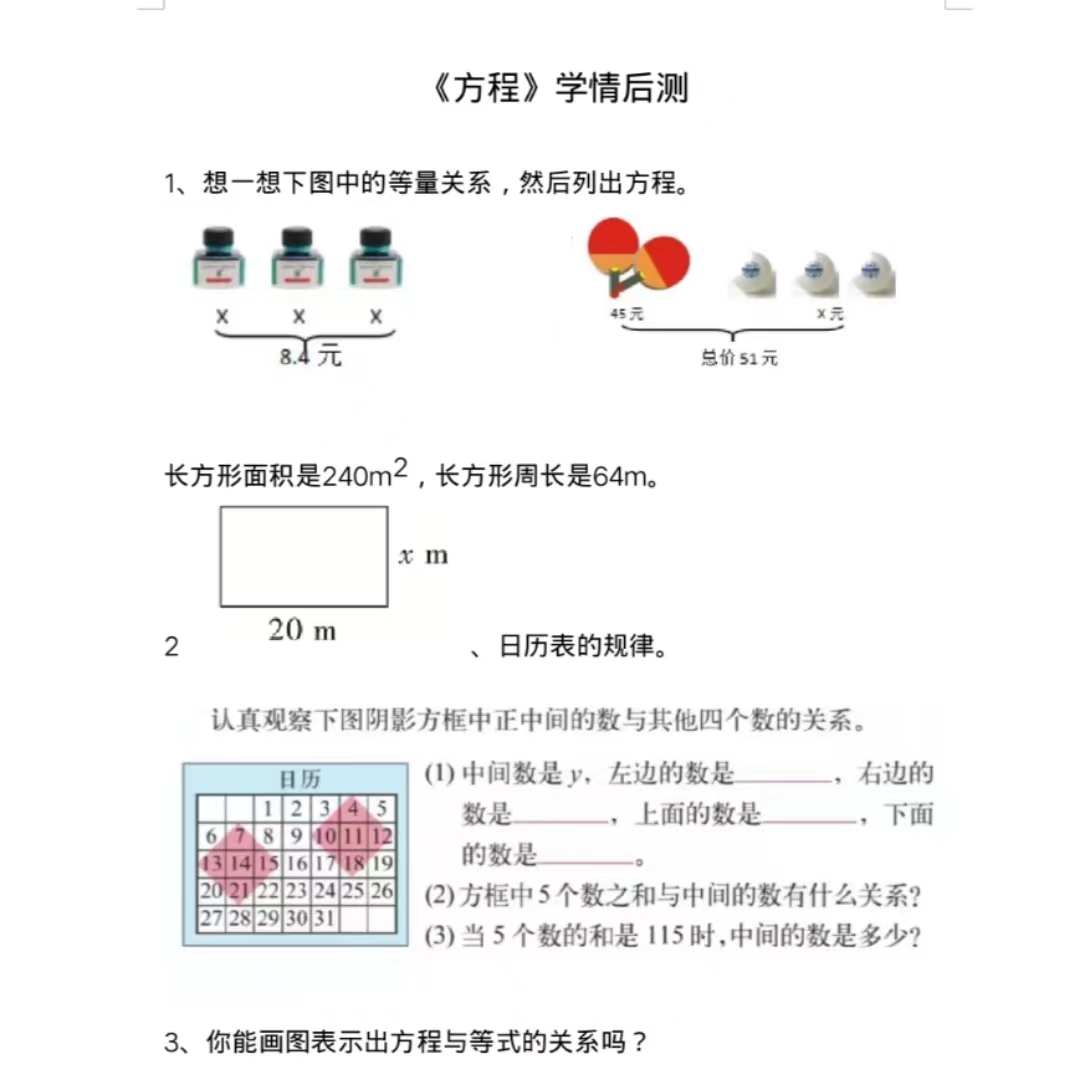
《方程》后测数据分析
第 1 题为 “基础题”。让学生通过读懂图意,然后找到等量关系式,并列出方程。
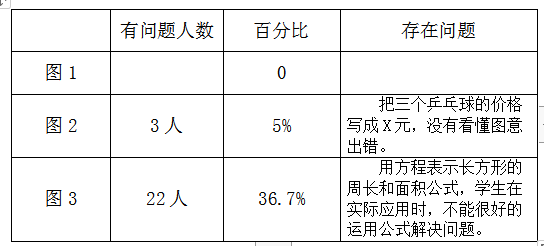
测试数据表明:对于基础的列方程学生都已基本掌握,但是,当在利用方程知识解决实际图形的相关计算时,学生出现了各种错误,在公式应用方面还是有一定的难度。
第 2 题为 “思维拓展题”。日历中的规律,学生在三年级的基础上再次接触,对部分学生来说,知识内容有一定的遗忘。第(1)小题寻找日历中尽可能多的规律,并尝试用字母表示出来,在这个问题的完成上,大多数孩子的表现比较棒,都能正确运用字母和规律正确完成填空。
第(2)小题,方框中的 5 个数之和与中间的数有什么关系?这个问题对学生来说是有一定难度的,从完成反馈来看,学生出错的比较多,需要教师进一步引导,发现规律并运用规律解决问题。
理解了第(2)小题中的规律后,再解决第(3)小题的问题,学生相对来说就轻松许多,直接根据前面找到的规律进行验证即可。
让学生在探索日历规律的基础上,发现等量关系,并列出方程。
第 3 题: 你能画图表示出方程与等式的关系吗?这道题考查学生对方程和等式之间知识的链接,从学生作答情况来看,多数孩子对方程意义的理解浮于表象,没有深度理解方程的意义,所以在画图时出现困难。
所以说,方程不仅仅是学生的头脑中存在的具体的表象。而是在具体情境的引导下,在解决问题的过程中,让方程变得不再遥远,并逐步提升对方程的深层次理解和应用。
教案终稿:
方程
执教教师:贾智媛 山西省运城市临猗县猗氏镇贵戚坊小学校 (百所示范校)
答辩成员:张勤奋 山西省运城市临猗县猗氏镇贵戚坊小学校 (百所示范校)
荆 茹 山西省运城市临猗县猗氏镇贵戚坊小学校 (百所示范校)
曹 洁 山西省运城市临猗县猗氏镇贵戚坊小学校 (百所示范校)
指导教师:何晓娜 山西省运城市临猗县教研室
陈 姣 山西省运城市临猗县贵戚坊小学校 (百所示范校)
【答辩团队风采展示】

【教学内容】
新世纪小学数学(北师大版)四年级下册 66~67 页
【教材分析】
学生在以往的数学学习过程中,常见填括号的等式,也就是填写未知的数,这正是学生学习方程的知识基础。同时《方程》一课是在学生已经学习了《字母表示数》、《等量关系》的基础上编排的。为了使学生体会方程是刻画现实世界的有效数学模型,产生学习方程的欲望,教材设置了多方面的问题情境,引导学生亲身经历并探索将 “文字描述的等量关系” 转换成 “符号化的等量关系”。从具体到抽象,引导学生在观察、交流中理解方程的意义,为后续学习解方程、用方程解决问题奠定基础。
【学生分析】
为准确把握学习起点,我们对四年级 6 个班 380 位学生进行了教学前测。依托天平情境,能用简洁符号表示等量关系的占 88.1%;依托生活情境,能用简洁符号表示等量关系的占 57.3%;能用自己的语言说明什么是方程的占 12.6%。这些数据说明,大部分学生已经有了初步的符号意识,能在相对简单、具体的情境中主动运用符号。对于 “方程” 这两个字的认识,绝大多数孩子更是不知从何谈起。前测中最后一个问题 “x+2=10 可以用来表示什么?”,学生借助天平来表示的占 51.8%,画图表示的占 23.4%,用文字来表示的占 17.3%。在将这个等式丰富化的过程中,更进一步验证了以上分析。可以说直观、形象、易操作的天平在学生的头脑中存在具体的表象,方程变得不再遥远和神秘,甚至可以成为他们心中方程的代名词。
【学习目标】
1. 结合具体情境了解方程的意义,会用方程表示简单情境中的等量关系。
2. 经历将现实问题抽象成等式与方程的过程,积累将等量关系符号化的活动经验。
3. 在丰富的问题情境中感受生活中存在大量的等量关系,体验数学与生活的密切联系。
【教学过程】
一、链接旧知,激活符号经验
1. 上节课我们学习了等量关系,那你能找出这三幅图中的等量关系吗?
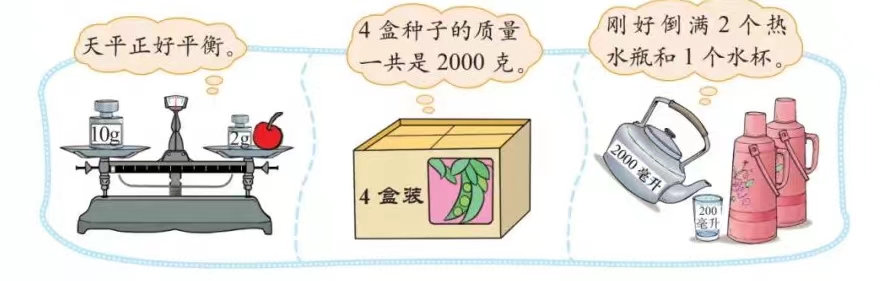
独立思考 1 分钟后,同桌交流。
(1)10 克 = 一个樱桃的质量 + 2 克。
(2)每盒种子的质量 ×4=2000 克。
(3)2000 毫升 = 每个热水瓶的盛水量 ×2+200 毫升。
小结:看来,大家都能灵活运用运算符号,条理的表示出图中的等量关系。
【设计意图】本节课是在学生学习了 “用字母表示数” 和 “等量关系” 的基础上进行教学的,找出 “等量关系” 是列方程的核心。另一方面在评价环节强调运用多种运算符号表示等量关系,初步使学生经历由文字描述图中信息到符号代替的过程,培养学生的符号意识。
二、实践体验,发展符号意识
活动一:自主尝试,简洁刻画
你能用简洁的式子,表示第一幅图中的等量关系吗?
1. 独立思考:学生尝试用自己喜欢的符号,把长长的等量关系,用自己认为最简洁的方式表示出来。
2. 展示交流:挑选代表性作品,请学生分享自己的想法。
3. 数学史源:笛卡尔是法国数学家,他曾提出用字母 x、y、z 表示不知道的数,这种方法沿用至今。
小结:大家都能用自己喜欢的符号,表示出樱桃的质量,并用简洁的式子表示出了图中的等量关系,特别是有些同学和数学家笛卡尔的想法不谋而合。(板书:10=x+2)
【设计意图】数学符号的引入,可以简短地表示和反映数量关系。所以让学生经历 “从具体事物→学生个性化的符号表示→学会数学地表示” 这一逐步符号化的过程,感受符号的多样性和必要性,并借助数学史源,理解使用数学符号的作用和价值。
活动二:丰富情境,深化理解
你能像这样,表示其他的等量关系吗?请看后两幅图。(独立思考 1 分钟后,小组内交流自己方法)
【设计意图】在学生经历用简洁的式子表示等量关系之后,脱离天平载体,丰富图中情境,使学生进一步体会使用符号表示等量关系的优越性,感悟运用符号刻画等量关系的方法。同时,在追问与表达的过程中,引导学生进一步深入思考,体会符号的运用对于数学表达的积极意义,深化学生对符号的进一步认识和理解。
活动三:归纳总结,认识方程。
仔细观察上面的式子,有什么共同之处?
1. 对比观察:都有等号、都含有字母。
2. 启发思考:这些字母表示什么?
3. 共同总结:含有未知数的等式叫方程。
4. 追问本质:判断一个式子是不是方程,需要具备哪些条件?
【设计意图】在学生学会用简洁的式子表达等量关系之后,引导学生在对比观察、合作交流、思考辨析中,认识并寻找方程的关键特征 ——“含有未知数” 与 “等式”,从而体会符号的作用,理解方程意义中最重要的内涵。
活动四:串联旧知,感受思想
1. 从一年级开始方程就藏在我们身边了。
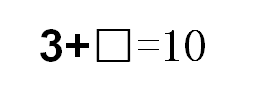
2. 二年级时我们也学过方程。你能找到等量关系,并列出方程吗?
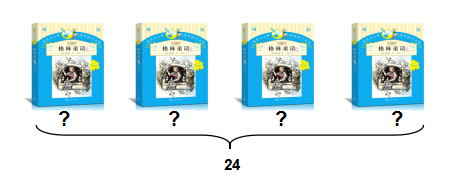
3. 三年级也接触过方程,你能用方程表示下列图中的等量关系吗?
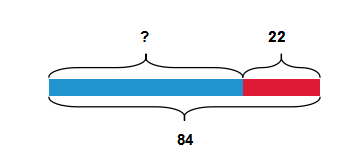
4. 而到了四年级,通过字母表示数和等量关系帮助我们认识了方程,而方程以后也会帮助我们更好的解决问题。
【设计意图】在学生认识了方程的形式特征的基础上,让学生重回起点,站在新的高度重新审视,进行新的思考。此环节的设计,将方程的教学置于由易到难、螺旋上升的整体性知识系统中,强调方程就是在已知与未知之间建立等量关系,凸显方程的建模本质。
三、综合应用,巩固提升符号意识
1. 先说一说图中的等量关系,再列出方程。
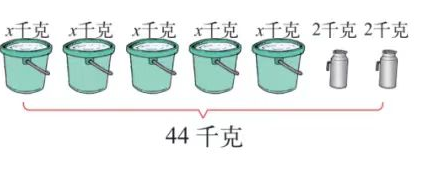
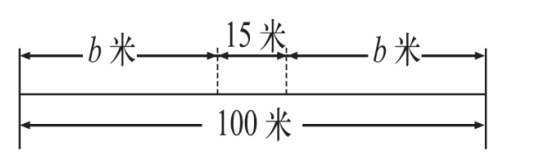
2. 你能根据图意列出方程吗?

3. 请你写出一个方程,然后说一说这个方程的意义。
【设计意图】练习题的设计,注重分层次,帮助学生再次理解方程的意义,在利用方程知识解决数学问题的过程中,不断丰富方程的涵义,感悟模型思想的本质,积累数学活动经验,更有利于提升学生发现、提出、分析、解决问题的能力。
四、联系生活,激发符号意识
孩子们,我们认识了方程,那你知道方程是怎么演变来的呢?播放视频《方程发展史》。
小结:现在,大家一定对方程有了更多的了解,它不仅历史悠久,而且随着我们知识的积累,运用方程解决越复杂的问题,它的优势就会愈加明显,这就是方程的魅力所在。
【设计意图】让学生了解方程的产生与发展过程,以及数学与人类文明进步的联系,凸显数学的文化特征,感受数学魅力。
【教学设计点评】
“含有未知数的等式叫做方程”,是当前我国小学数学教材普遍采用的 “方程” 定义。然而,西南师范大学著名数学家陈重穆教授等曾撰文呼吁:“含有未知数的等式叫做方程” 这样的定义要淡化,不要记,无须背,更不要考。那么,方程教学的核心在哪里?学习方程的价值是什么?贾老师的课做了一些有意义的探索:
一、依托等量关系,建构方程模型
方程是刻画现实世界的一个有效的数学模型,方程的本质特征是等量关系,它的核心在于建模。如果仅仅从生活实际引入方程的学习,学生只观察到了其 “形” 而未触及到 “核”,因此,课伊始,贾老师借助三幅不同层次的情境图,让学生借助真实情境去理解等量关系,在观察、思考、交流、对话等一系列活动中,用等式表示已知数和未知数之间客观存在的等量关系,并且全课一直紧紧围绕 “等量关系” 这一核心,丰富学生的感知,积累思维经验,从而初步建构方程的模型。
二、经历探究过程,发展符号意识
方程教学是在学生学了四年的算术知识,初步接触了一点代数知识基础上进行学习的,学生在此之前,对于方程的意义已经有了初步的感知,例如填算式中的括号、看图列算式等等,这些其实就是方程最初的 “萌芽”。课堂上,贾老师充分放手,让学生自己尝试用简洁的式子表示出等量关系,学生亲身经历了观察现象 —— 语言表达 —— 符号表达的全过程,逐步完善对方程特征的构建,方程的理解由模糊到清晰,思维的发展由具体到抽象。在此过程中,学生运用符号表示数量关系,初步感悟符号的数学功能,从而有效发展了学生的符号意识。
三、淡化方程概念,渗透数学文化
我们常常有这样的感觉:学生学习完方程之后,常常不愿意用方程解决问题,无法体会方程的优越性,原因就在于传统的教学过于追求方程的定义,忽视方程的核心价值。从贾老师的课堂我们可以看出,自始至终,全课没有追求对方程定义的过分关注,没有让学生去判断是不是方程,去背方程的定义,而是淡化方程的定义,引领学生理解方程的本质,经历方程的形成过程,让学生在比较辨析的基础上,尝试给方程 “下定义”;在回顾、分析、唤醒的过程中,深刻理解方程的内涵,即表示的是未知数和已知数之间建立的一种等量关系;通过资料让学生了解方程的发展史,把数学文化融入课堂教学中,让学生对方程的产生过程有清晰的认识,真正用方程的核心价值去打动学生。
总之,让学生从丰富多样的现实具体问题中,抽象出 “方程” 这一模型,经历概念的形成过程,真正凸显方程的核心价值。可以说,这样的 “方程” 教学,真正的把现实问题抽象为数学模型,把生活世界引向符号世界。
【我对符号意识的理解】
《义务教育数学课程标准》(2022 版)指出:符号意识主要是指能够感悟符号的数学功能。知道符号表达的现实意义,能够初步运用符号表示数量、关系和一般规律;知道用符号表达的运算规律和推理结论具有一般性;初步体会符号的使用是数学表达和数学思考的重要形式,符号意识是形成抽象能力和推理能力的经验基础。
基于此并通过研读有关 “符号意识” 文献和执教《方程》一课教学感悟,我对符号意识理解如下:
1. 符号是数学的语言。是人们进行表达、计算、推理、交流和解决问题的工具,学习数学的目的之一是要使学生懂得符号的意义,会运用符号解决实际问题,发展学生的符号意识。英国著名数学家罗素曾说过:“数学就是符号加逻辑。” 可见,数学符号在学习数学中有着举足轻重的地位。在具体情境中培养学生的 “符号意识”,其实就是教给学生在数学王国中巡游的方法。
2. 学生在生活中接触很多用符号来表示的情境,使学生积存了很多潜藏的 “符号意识”,这是培养学生符号意识的重要基础。数学符号的学习过程应遵循从感性到理性运用的辩证过程。因此,教学中教师可以关注学生已有的符号经验,将数学教学设计成看得见、摸得着的物质化实践活动,在解决问题中熟练符号的使用;也要根据学生的认知特点,帮助学生理顺数学概念、规律等符号化的一般关系,从体验到理解运用,再从理解运用到按需要创新来培养学生 “符号思想”,提升符号意识!
3. 在《方程》一课中,让学生用最简洁的方式表示等量关系,意图在于引导学生经历 “从具体事物→学生个性化的符号表示→学会数学地表示” 这一逐步符号化的过程,感受引入符号的必要性,同时在对数学符号的语言表达和思考方面,渗透简洁性和简单美,理解数学符号的作用和价值。
【思考在延伸】
1. 学习方程的价值在于用方程解决问题,如何在方程教学中渗透这一理念?
2. 和算术相比,方程是由已知走向未知,是一种顺向思考,从解决问题的策略来说,方程比算术更方便。在小学的课堂中,我们如何引导学生体会方程这一核心价值?
【教材图片】
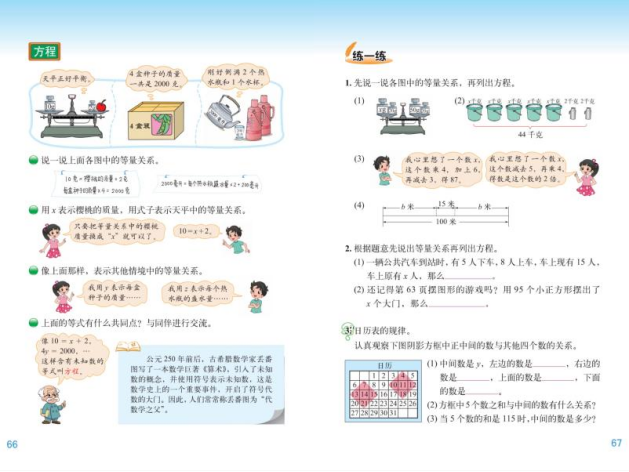
贾老师在教学中利用等量关系构造方程模型,让学生经历以 “问题情境 ——— 已知数、未知数、等量关系 ——— 建立方程(模型)” 的数学活动过程,不断丰富 “方程表示已知数与未知数之间的等量关系” 的涵义,感悟模型思想的本质,积累数学活动经验,这样的教学设计更有利于学生去发现、提出、分析、解决问题,培养创新意识。
贾老师在本课通过引入字母表示现实生活中的未知数,并用等式表示未知数与已知数之间客观存在的等量关系,建立对方程的初步认识;从数学符号的角度分析,方程又是数量符号、运算符号、关系符号等多种数学符号的有效结合。
本节课是在学生学习了 “用字母表示数” 和 “等量关系” 的基础上进行教学的,找出 “等量关系” 是列方程的核心。贾老师链接旧知,让孩子先寻找图中的等量关系,再让孩子尝试用简洁的式子表示事物的等量关系,逐步上升,从而引出方程。