教案终稿：

方程

执教教师：贾智媛 山西省运城市临猗县猗氏镇贵戚坊小学校 (百所示范校）

答辩成员：张勤奋  山西省运城市临猗县猗氏镇贵戚坊小学校 (百所示范校）

荆  茹  山西省运城市临猗县猗氏镇贵戚坊小学校 (百所示范校）

曹  洁  山西省运城市临猗县猗氏镇贵戚坊小学校 (百所示范校）

指导教师：何晓娜  山西省运城市临猗县教研室

陈  姣  山西省运城市临猗县贵戚坊小学校 (百所示范校）

【答辩团队风采展示】

【教学内容】

新世纪小学数学（北师大版）四年级下册 66～67 页

【教材分析】

学生在以往的数学学习过程中，常见填括号的等式，也就是填写未知的数，这正是学生学习方程的知识基础。同时《方程》一课是在学生已经学习了《字母表示数》、《等量关系》的基础上编排的。为了使学生体会方程是刻画现实世界的有效数学模型，产生学习方程的欲望，教材设置了多方面的问题情境，引导学生亲身经历并探索将 “文字描述的等量关系” 转换成 “符号化的等量关系”。从具体到抽象，引导学生在观察、交流中理解方程的意义，为后续学习解方程、用方程解决问题奠定基础。

【学生分析】

为准确把握学习起点，我们对四年级 6 个班 380 位学生进行了教学前测。依托天平情境，能用简洁符号表示等量关系的占 88.1%；依托生活情境，能用简洁符号表示等量关系的占 57.3%；能用自己的语言说明什么是方程的占 12.6%。这些数据说明，大部分学生已经有了初步的符号意识，能在相对简单、具体的情境中主动运用符号。对于 “方程” 这两个字的认识，绝大多数孩子更是不知从何谈起。前测中最后一个问题 “x+2=10 可以用来表示什么？”，学生借助天平来表示的占 51.8%，画图表示的占 23.4%，用文字来表示的占 17.3%。在将这个等式丰富化的过程中，更进一步验证了以上分析。可以说直观、形象、易操作的天平在学生的头脑中存在具体的表象，方程变得不再遥远和神秘，甚至可以成为他们心中方程的代名词。

【学习目标】

1. 结合具体情境了解方程的意义，会用方程表示简单情境中的等量关系。

2. 经历将现实问题抽象成等式与方程的过程，积累将等量关系符号化的活动经验。

3. 在丰富的问题情境中感受生活中存在大量的等量关系，体验数学与生活的密切联系。

【教学过程】

一、链接旧知，激活符号经验

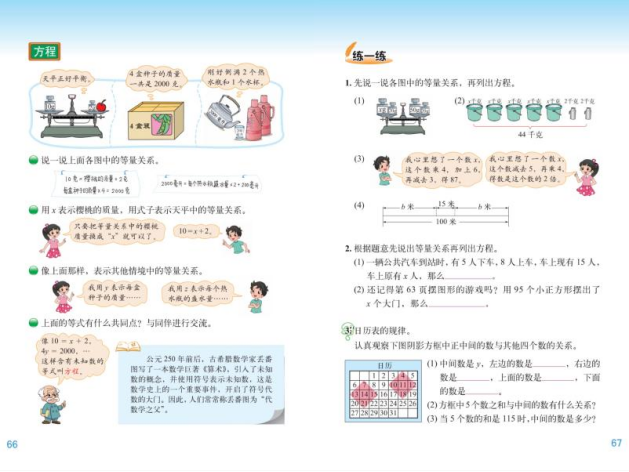
1. 上节课我们学习了等量关系，那你能找出这三幅图中的等量关系吗？

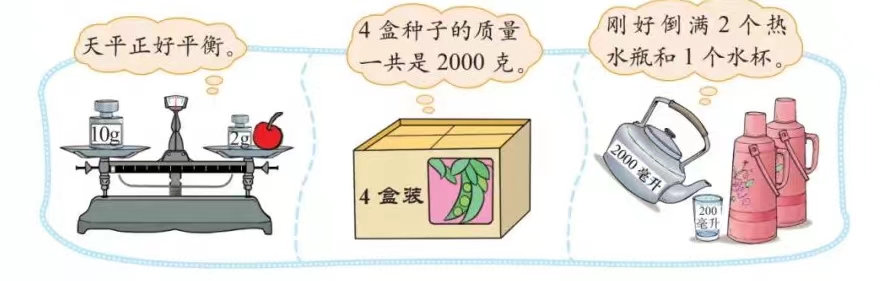
独立思考 1 分钟后，同桌交流。

（1）10 克 = 一个樱桃的质量 + 2 克。

（2）每盒种子的质量 ×4=2000 克。

（3）2000 毫升 = 每个热水瓶的盛水量 ×2+200 毫升。

小结：看来，大家都能灵活运用运算符号，条理的表示出图中的等量关系。

【设计意图】本节课是在学生学习了 “用字母表示数” 和 “等量关系” 的基础上进行教学的，找出 “等量关系” 是列方程的核心。另一方面在评价环节强调运用多种运算符号表示等量关系，初步使学生经历由文字描述图中信息到符号代替的过程，培养学生的符号意识。

二、实践体验，发展符号意识

活动一：自主尝试，简洁刻画

你能用简洁的式子，表示第一幅图中的等量关系吗？

1. 独立思考：学生尝试用自己喜欢的符号，把长长的等量关系，用自己认为最简洁的方式表示出来。

2. 展示交流：挑选代表性作品，请学生分享自己的想法。

3. 数学史源：笛卡尔是法国数学家，他曾提出用字母 x、y、z 表示不知道的数，这种方法沿用至今。

小结：大家都能用自己喜欢的符号，表示出樱桃的质量，并用简洁的式子表示出了图中的等量关系，特别是有些同学和数学家笛卡尔的想法不谋而合。（板书：10=x+2）

【设计意图】数学符号的引入，可以简短地表示和反映数量关系。所以让学生经历 “从具体事物→学生个性化的符号表示→学会数学地表示” 这一逐步符号化的过程，感受符号的多样性和必要性，并借助数学史源，理解使用数学符号的作用和价值。

活动二：丰富情境，深化理解

你能像这样，表示其他的等量关系吗？请看后两幅图。（独立思考 1 分钟后，小组内交流自己方法）

【设计意图】在学生经历用简洁的式子表示等量关系之后，脱离天平载体，丰富图中情境，使学生进一步体会使用符号表示等量关系的优越性，感悟运用符号刻画等量关系的方法。同时，在追问与表达的过程中，引导学生进一步深入思考，体会符号的运用对于数学表达的积极意义，深化学生对符号的进一步认识和理解。

活动三：归纳总结，认识方程。

仔细观察上面的式子，有什么共同之处？

1. 对比观察：都有等号、都含有字母。

2. 启发思考：这些字母表示什么？

3. 共同总结：含有未知数的等式叫方程。

4. 追问本质：判断一个式子是不是方程，需要具备哪些条件？

【设计意图】在学生学会用简洁的式子表达等量关系之后，引导学生在对比观察、合作交流、思考辨析中，认识并寻找方程的关键特征 ——“含有未知数” 与 “等式”，从而体会符号的作用，理解方程意义中最重要的内涵。

活动四：串联旧知，感受思想

1. 从一年级开始方程就藏在我们身边了。

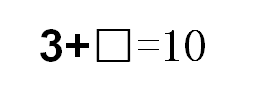
2. 二年级时我们也学过方程。你能找到等量关系，并列出方程吗？

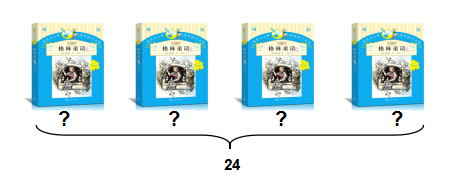
3. 三年级也接触过方程，你能用方程表示下列图中的等量关系吗？

4. 而到了四年级，通过字母表示数和等量关系帮助我们认识了方程，而方程以后也会帮助我们更好的解决问题。

【设计意图】在学生认识了方程的形式特征的基础上，让学生重回起点，站在新的高度重新审视，进行新的思考。此环节的设计，将方程的教学置于由易到难、螺旋上升的整体性知识系统中，强调方程就是在已知与未知之间建立等量关系，凸显方程的建模本质。

三、综合应用，巩固提升符号意识

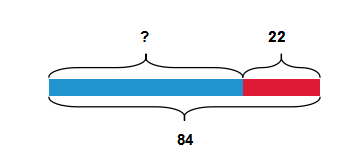
1. 先说一说图中的等量关系，再列出方程。

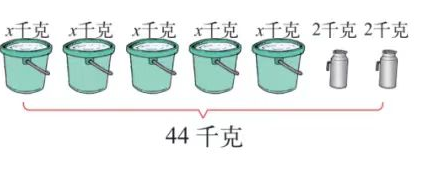
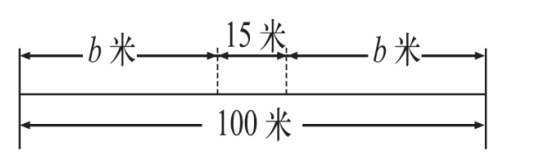
2. 你能根据图意列出方程吗？

3. 请你写出一个方程，然后说一说这个方程的意义。

【设计意图】练习题的设计，注重分层次，帮助学生再次理解方程的意义，在利用方程知识解决数学问题的过程中，不断丰富方程的涵义，感悟模型思想的本质，积累数学活动经验，更有利于提升学生发现、提出、分析、解决问题的能力。

四、联系生活，激发符号意识

孩子们，我们认识了方程，那你知道方程是怎么演变来的呢？播放视频《方程发展史》。

小结：现在，大家一定对方程有了更多的了解，它不仅历史悠久，而且随着我们知识的积累，运用方程解决越复杂的问题，它的优势就会愈加明显，这就是方程的魅力所在。

【设计意图】让学生了解方程的产生与发展过程，以及数学与人类文明进步的联系，凸显数学的文化特征，感受数学魅力。

【教学设计点评】

“含有未知数的等式叫做方程”，是当前我国小学数学教材普遍采用的 “方程” 定义。然而，西南师范大学著名数学家陈重穆教授等曾撰文呼吁：“含有未知数的等式叫做方程” 这样的定义要淡化，不要记，无须背，更不要考。那么，方程教学的核心在哪里？学习方程的价值是什么？贾老师的课做了一些有意义的探索：

一、依托等量关系，建构方程模型

方程是刻画现实世界的一个有效的数学模型，方程的本质特征是等量关系，它的核心在于建模。如果仅仅从生活实际引入方程的学习，学生只观察到了其 “形” 而未触及到 “核”，因此，课伊始，贾老师借助三幅不同层次的情境图，让学生借助真实情境去理解等量关系，在观察、思考、交流、对话等一系列活动中，用等式表示已知数和未知数之间客观存在的等量关系，并且全课一直紧紧围绕 “等量关系” 这一核心，丰富学生的感知，积累思维经验，从而初步建构方程的模型。

二、经历探究过程，发展符号意识

方程教学是在学生学了四年的算术知识，初步接触了一点代数知识基础上进行学习的，学生在此之前，对于方程的意义已经有了初步的感知，例如填算式中的括号、看图列算式等等，这些其实就是方程最初的 “萌芽”。课堂上，贾老师充分放手，让学生自己尝试用简洁的式子表示出等量关系，学生亲身经历了观察现象 —— 语言表达 —— 符号表达的全过程，逐步完善对方程特征的构建，方程的理解由模糊到清晰，思维的发展由具体到抽象。在此过程中，学生运用符号表示数量关系，初步感悟符号的数学功能，从而有效发展了学生的符号意识。

三、淡化方程概念，渗透数学文化

我们常常有这样的感觉：学生学习完方程之后，常常不愿意用方程解决问题，无法体会方程的优越性，原因就在于传统的教学过于追求方程的定义，忽视方程的核心价值。从贾老师的课堂我们可以看出，自始至终，全课没有追求对方程定义的过分关注，没有让学生去判断是不是方程，去背方程的定义，而是淡化方程的定义，引领学生理解方程的本质，经历方程的形成过程，让学生在比较辨析的基础上，尝试给方程 “下定义”；在回顾、分析、唤醒的过程中，深刻理解方程的内涵，即表示的是未知数和已知数之间建立的一种等量关系；通过资料让学生了解方程的发展史，把数学文化融入课堂教学中，让学生对方程的产生过程有清晰的认识，真正用方程的核心价值去打动学生。

总之，让学生从丰富多样的现实具体问题中，抽象出 “方程” 这一模型，经历概念的形成过程，真正凸显方程的核心价值。可以说，这样的 “方程” 教学，真正的把现实问题抽象为数学模型，把生活世界引向符号世界。

【我对符号意识的理解】

《义务教育数学课程标准》（2022 版）指出：符号意识主要是指能够感悟符号的数学功能。知道符号表达的现实意义，能够初步运用符号表示数量、关系和一般规律；知道用符号表达的运算规律和推理结论具有一般性；初步体会符号的使用是数学表达和数学思考的重要形式，符号意识是形成抽象能力和推理能力的经验基础。

基于此并通过研读有关 “符号意识” 文献和执教《方程》一课教学感悟，我对符号意识理解如下：

1. 符号是数学的语言。是人们进行表达、计算、推理、交流和解决问题的工具，学习数学的目的之一是要使学生懂得符号的意义，会运用符号解决实际问题，发展学生的符号意识。英国著名数学家罗素曾说过：“数学就是符号加逻辑。” 可见，数学符号在学习数学中有着举足轻重的地位。在具体情境中培养学生的 “符号意识”，其实就是教给学生在数学王国中巡游的方法。  

2. 学生在生活中接触很多用符号来表示的情境，使学生积存了很多潜藏的 “符号意识”，这是培养学生符号意识的重要基础。数学符号的学习过程应遵循从感性到理性运用的辩证过程。因此，教学中教师可以关注学生已有的符号经验，将数学教学设计成看得见、摸得着的物质化实践活动，在解决问题中熟练符号的使用；也要根据学生的认知特点，帮助学生理顺数学概念、规律等符号化的一般关系，从体验到理解运用，再从理解运用到按需要创新来培养学生 “符号思想”，提升符号意识！

3. 在《方程》一课中，让学生用最简洁的方式表示等量关系，意图在于引导学生经历 “从具体事物→学生个性化的符号表示→学会数学地表示” 这一逐步符号化的过程，感受引入符号的必要性，同时在对数学符号的语言表达和思考方面，渗透简洁性和简单美，理解数学符号的作用和价值。

【思考在延伸】

1. 学习方程的价值在于用方程解决问题，如何在方程教学中渗透这一理念？

2. 和算术相比，方程是由已知走向未知，是一种顺向思考，从解决问题的策略来说，方程比算术更方便。在小学的课堂中，我们如何引导学生体会方程这一核心价值？

【教材图片】