【2020秋】四川成都都江堰代益梅工作室代益梅四下《探索与发现：三角形内角和》

1. 教材图片

2.【主题、教材、学情分析】

一、关于主题 “混合式学习” 的解读：

突如其来的新冠疫情，使国内外上下掀起了 "停课不停学" 的在线学习浪潮，为全面、正式构建一种新的学习形态 “混合式学习” 提供了尝试。在小学数学学习中，在线学习无法完全替代师生面对面的线下课堂学习，但国内外疫情防控形势依然严峻的当下，可以预见，线上与线下有机融合的混合式学习将成为未来学习的重要方式，并且离我们越来越近。感谢组委会提出 “混合式学习” 这个主题，让我们团队开启了啃书模式，相信随着研究的进一步深入，我们对混合式学习的理解也会越来越深，那么，什么是混合式学习呢？我们团队通过检索知网发现：文献题目主题中含有 “混合式学习” 关键词的中文文献国内有 1654 篇，含有 “blended learning” 的英文文献有 1088 篇。“混合式学习模式” 的有 518 篇，“混合式学习理论” 的有 32 篇。其中，多为高等院校和中学案例，小学案例少之又少。接着我们先后购买了《混合式学习：用颠覆式创新推动教育革命》和《混合式教学：技术工具辅助教学实操手册》两本混合式学习的专著，又在知网上学习了《上海教育》关于 “混合式学习” 的主题专栏文章，还参考了《小学数学教育》、《小学数学教师》等名师的案例，对混合式学习有了进一步的了解。（......）

二、教材分析：

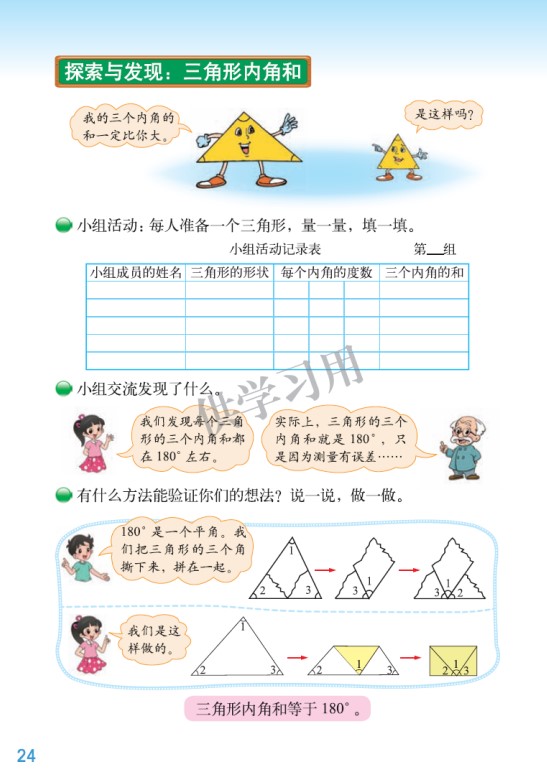
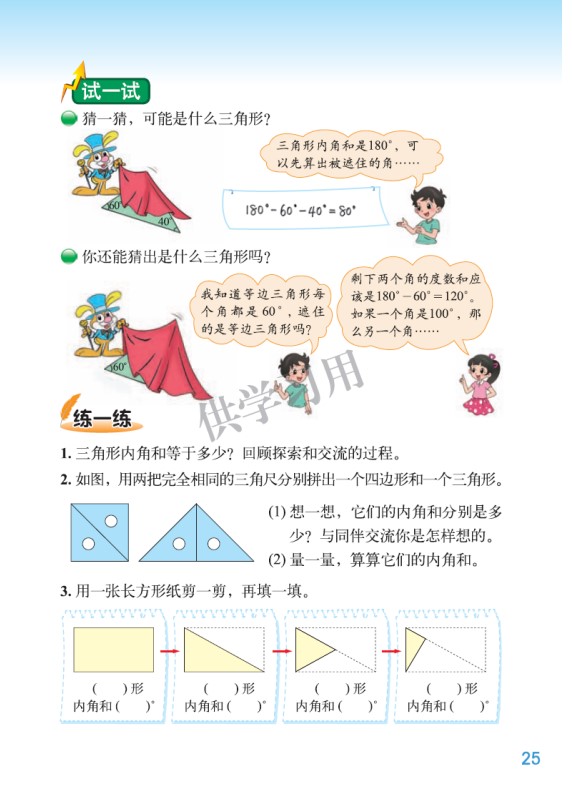
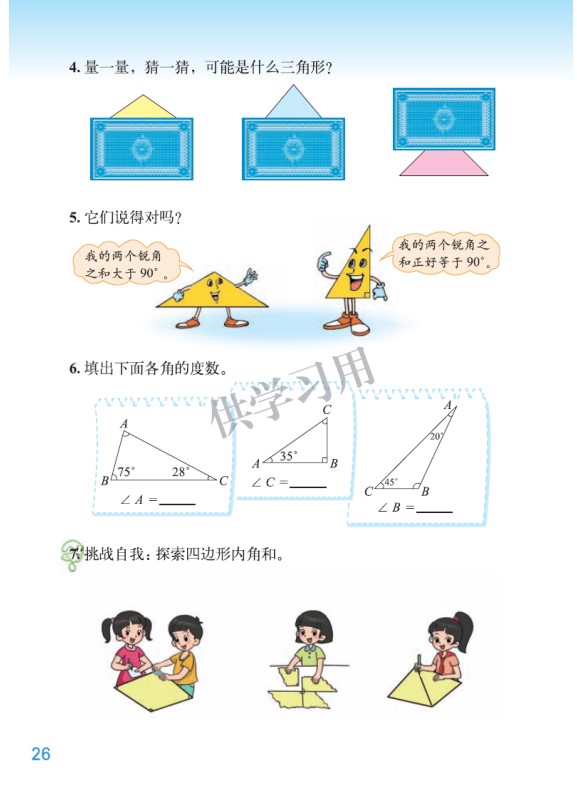
新世纪北师大教材四下《探索与发现：三角形内角和》一课，按照 “创设情境、解决问题、进行验证” 思路进行编排的。首先，创设形状和大小不同的三角形对内角和的争论，激发学生兴趣和思考，也引出下面学生对三角形内角和的探索活动。通过三个小绿点提出的三个问题，层层递进，从量角 -- 求和 -- 明晰 -- 验证，经历一系列的探究活动，最终发现并验证：三角形内角和等于 180°。随后在试一试还安排了运用三角形内角和性质来解决一些简单的实际问题。
同时，我们还比对了人教版、西师版、苏教版等教材，发现教材的编排大体分为两种思路：一种是分为侧重操作验证探究来编排，比如人教版、北师大版、苏教版和青岛版等；一种是侧重推理验证探究来编排，比如台湾等地区教材。
我们结合两种编排思路，既想体现 “探究性学习” 中学生的多元操作验证，又想抓住数学基本思想 “推理” 来验证，渗透数学文化，培养学生的理性思维。
（......）

三、学情分析：

学生在二年级初步学习了《认识角》，四年级上册学习了《角的再认识》，四年级下册学习了《三角形的分类》等，已经会标角、度量角、画角，也有一定的量角的活动经验和计算能力。通过课前调研学情发现：部分孩子们是知道 “三角形内角和等于 180°” 这条结论的，从老师、家长、校外机构、书本等渠道知道的；而一些孩子知道三角形内角和是 100 多度；个别孩子不知道这个知识。知其然而不知其所以然 —— 暴露出了孩子的真实学情，这就为探索活动奠定了良好的基础。
我们先后设计了几个版本的课前首学单，并不断根据试教情况进行改进。在某一次的课前前置首学统计中，我们发现：该次 45 人参与（1 人特殊儿童），44 人会标三角形的内角；仅有 18 人知道三角形内角和是 180°，有 23 人说三角形内角和在 9° 至 310° 之间，有 2 人说不知道，有 1 人说三角形内角和是 3-5 厘米。虽然这个班学生基础比较薄弱，但是我们万万没想到会有如此 “多元” 的、原生态的内角和理解。
（......）

四、资源分析：

国内疫情发生过后，由新世纪小学数学主编刘坚教授发起并组织编委会工作人员和全国一线教师们，开始新世纪北师大教材配套微课 3.0 的制作。我们团队中的 4 位小伙伴有幸参与到其中，不仅经历了对微课脚本撰写 “本质” 认识的飞跃，而且更难得的是深度解读了教材编者的 “每个小绿点” 背后的意图，彻底更新了 “以生为本”、教师引领的观念。而这节 3.0 版的微课《探索与发现：三角形内角和》，不仅有编委会工作室精心制作的 MG 动画微课，还有一线教师在后面补充的针对性练习和学生答题视频分享。不论从制作技术还是内容呈现上，这节微课都能很好地作为线上学习资源，激发孩子们的探究兴趣和欲望，这是我们团队选择这节微课的原因之一。
此外，结合疫情期间学生线上学习的相关情况，我们选取了前面开课到 4 分 32 秒的微课 3.0 片段，作为孩子课前自学的资源，请孩子观看微课后，根据微课中的测量方法，测量出老师发给孩子们人手一个的三角形，并填写相关数据在首学单上，同时提出发现和疑问。
（......）

3.【教学设计第一稿】

学习目标：

1. 通过量、剪、拼、折等直观操作活动，探索并发现三角形内角和等于 180°，发展动手操作、观察比较的能力。
2. 能运用三角形内角和的性质解决一些简单的实际问题。
3. 在亲历探索发现的过程中，体验数学思考与探究的乐趣，培养学习数学的兴趣。
学习重点：让学生经历知识形成、发展和应用的全过程，并会运用知识解决问题。
学习难点：量角带来的误差；探索验证方法的多样性。
学习准备：3.0 微课片段、PPT、学习单、操作材料包。


学习过程：
一、创设情境，激趣引入
1. 复习旧知，引出新知。复习锐角三角形、直角三角形、钝角三角形。
2. 学习微课片段 —— 三角形争论内角和大小，激发学生探究欲望。
【设计意图】通过复习旧知，打通学生知识的串联，关联知识的结构化。借助 3.0 微课的动画效果，激发学生思考：一千个 “三角形” 会不会有一千个 “内角和”？


二、初试四学 —— 度量入手，聚焦发现
（一）首学：自主度量 —— 三角形内角和。
1. 在首学单上，任意画一个喜欢的三角形，标出 3 个内角。
2. 用量角器度量出三个内角的度数，记录下来，计算出三个内角的和。
（二）互学：小组交流发现。
预设：
1. 三角形内角和度数百花齐放。
2. 三角形的内角和是 180° 左右。
（三）群学：集体交流。
预设：三种不同的三角形（直、锐、钝）度数呈现。
聚焦：为什么会产生这样的误差？
（四）共学：用电脑微课或 PPT 动画方式解决。
不量，有其它方法来验证吗？
【设计意图】学生利用已有的知识对内角进行测量并求和，使学生在测量过程中体会数学学习的严谨性，感受测量中的误差对结果的影响。


三、再次四学 —— 动手操作，验证发现
(一) 独立思考，小组讨论，尝试操作验证。
预设：剪（撕）、折等。
（二）汇报验证，小结方法，评价。
(三) 追问：为什么大小不一样的三角形内角和都是 180 度？为什么钝角三角形、锐角三角形、直角三角形形状不同，内角和也都是 180°？
预设：角的大小与边的长短无关；三种类型三角形角的辩证关系。
小结归纳：沟通方法间的联系和区别。
【设计意图】注重验证方法的多样性，鼓励学生大胆实验。

四、链接古今，渗透文化
链接法国数学家帕斯卡的故事
【设计意图】渗透数学文化，由操作验证走向推理验证

五、运用性质，解决问题
(一) 基础练习、解决 25 页练习题第 2 题。
(二) 拓展：四边形的内角和。
【设计意图】通过运用内角和性质来解决问题，学以致用，进一步明确 “内角” 的内涵，熟练进行性质的逆应用。在拓展练习过程中，注重知识、方法、思想的迁移。
 
 六、课堂总结。

4.【课前首学单第一稿】

课前首学单（一稿） 班级： 姓名：
1. 请你画一个三角形。并且在你画的三角形上表示出三角形的三个内角。

2. 你知道这三个内角的和是多少度吗？

3. 如果知道，你是从哪里知道三角形内角和这个知识的？

学习单 2（观看微课以后再填写）

1. 在《学习单 1》中，我画了一个三角形，通过测量，它的内角和是 ( ) 度. 算式:

2. 观看完微课，微课中的小朋友，他们测量出来的三角形内角和: 分别是 ( )、( )、( )、( )、( )。

3. 为什么大家测量出来的三角形内角和会不一样呢？ 我猜，可能是因为:
   。

5.【教学设计交流研讨 1 主要观点】

第一次试上后，师父郑大明老师提出：混合式学习的主题，一定要紧扣主题来构课；不能跟平时上课样态一样。

杜蓉老师提出：教师给学生自主的空间太少，牵着走的痕迹比较重，怎样能让孩子自主提出问题？

黄萍老师认为：是不是应该开课更加童趣一点，太直入主题。

李勇老师觉得：开课前面首学数据汇总太多，首学单建议改进，有点长。

胥平老师发现：学生小组合作操作不够直观醒目，应该改进。

李蓉老师说：教师语言过于繁琐琐碎，教学设计流程不够熟悉。

6.【教学设计二稿】

一、前置首学单。（线下首学 + 线上 3.0 微课）

（一）第一步，先完成线下首学单 1。乐教乐学平台推送上传

首学单 1 如下：

1. 请你画出一个三角形，标出它的三个内角.

2. 你知道三角形三个内角和是多少度吗？请写下来.

3. 你是通过什么方式知道的？

（二）第二步，观看微课 3.0 片段，完成线下首学单 2。

播放微课到 4 分 30 秒。思考出现这样情况的原因？

首学单 2 如下：

1. 在学习单 1 中，我画了一个三角形，通过测量，它的内角和是 ( ) 度。算式:------.

2. 观看完微课，微课中的小朋友，他们测量出来的三角形内角和， 分别是 ( )( )( )( )( ).

3. 为什么大家测量出来的三角形内角和会不一样呢？ 我猜，可能是因为:------.

【设计意图】：基于真实的学情出发，体会测量过程中因为 “误差” 带来的质疑？三角形内角和一定就是 180 度吗？怎么都测不到？既然操作探究得出的实验数据会受到误差的影响，那么还有没有另外的方式避免这样的 “误差” 呢？至于为什么要前置，发现 “测量” 是孩子们能够最先想到的、最普遍想到的方法。同时也发现全国部级一等奖优课，仅仅处理到操作得出结论，后面没有进一步处理到深度推理，时间就不够了，因此，把 “量 + 算” 的环节前置，为后边的操作探究和推理验证留足时间。

二、线下课堂学习过程。（操作探究 + 推理探究）演绎推理。

热身：合情推理的小故事：第一个芒果甜的；第二个，第三个，果园全都是甜的。（风险）

（一）首先解决前置学习的问题：

前置学情呈现，抽个别同学，全班梳理什么是内角？内角和？教具大号。

测量结果统计 VS 机灵狗问题？为什么会出现这样的情况？

学生全班汇总测量数据，智慧教室 IRS 投票汇总。

A. 比 170° 少 B.170-190° C. 比 190° 多的。

交流：什么原因？

全班汇报 —— 电脑 3.0 微课揭秘 “误差”。

（微课 3.0 播放 4 分 30 秒 ——5 分 55 秒验证，电脑验证）

【设计意图】：根据学生前测情况，展示前测真实学情，梳理问题，测量中的 “误差” 的问题为什么会出现？用信息技术手段解释 “误差” 的产生。从而引发学生思考：怎样验证避免出现误差？

（二）能用其它方式探究吗？避免误差。（撕拼、折拼等）

出示三个锦囊：

1 号锦囊：三角形 2 个，剪刀。（分类信封）

2 号锦囊：长方形 1 个，铅笔，三角板 2 个

3 号锦囊：6 个等边、不等边三角形。（分类信封）

1.1 号锦囊：

请拿出 1 号锦囊，6 个不同的三角形（直角 2 个、锐角 2 个、钝角 2 个），剪刀。交流方法。

提出要求：1. 先每人任意拿出 1 个三角形，标出它的 3 个内角。

2. 独立思考怎样验证 180？

3. 小组内交流，梳理出方法，作好汇报准备。（抢答）

群学汇报：请 2 个小组汇报

预设：撕 —— 拼、剪 —— 拼；折 —— 拼（不破坏）。

追问：凭什么撕下来放在一起就是 180°？凭什么折下来重合在一起就是 180°？

展示不同类型的三角形：每展示一次，

写：锐角三角形的内角和是 180°。 直角三角形的内角和是 180°。 钝角三角形的内角和是 180°。

大胆归纳：合情推理，能把这三句话说成一句话吗？每个三角形内角和 180 度？为什么？

【设计意图】：通过分类剪拼、撕拼，用合情推理归纳出结论，在推理的过程中，链接推理的核心关键 —— 把三个内角剪拼、撕拼成的图形是平角，因为平角是 180 度，所以三角形的内角和是 180 度。再根据角进行分类，我们把三角形分成了锐角三角形、钝角三角形和直角三角形，通过选取呈现不同的三角形，由特殊到一般，实现操作推理到抽象推理。

2.2 号锦囊：

继续追问残次品： 真心话，有没有同学的撕下来，折下来的是雀雀丫丫的？不像是平角呀？（又是 “误差”？）。可顺便让操作达人支支招：进行拼法、折法小贴士要点提醒。

挖坑：不能一而再，再而三地让 “误差” 来背锅呀？难道我们学数学学来让实验、操作背锅？思维的体操？再说又动手撕动手拼动手说还说不服我，还搞破坏？能不能简单点，就地取材，充分发挥数学思考的魅力，来说服我。

预设 1：如果在前面思考的过程中，有学生能联想到这个帕斯卡方法，就先放一边，请他此时展示。

预设 2：如果学生联想不到这个方法，进行提示。抽问？180° 联想到平角。180° 你还能联想到哪些特殊度数的角？360°

想不到？有一个小男孩想到了。

这个小男孩 12 岁，他随手拿起一张长方形纸，画了一条线，思考了一下，就对他的爸爸说：我好像发现了一个天大的秘密：三角形内角和是 180°。怎么回事呢？你敢来探索一下吗？锦囊 2 号。

独立思考，4 人互助，推理探索。

长方形内角和 360，两个直角三角形，每个 180 度。

PPT 文化渗透：数学史。说服我，你服吗？还要不要 “误差” 来背锅；以理服人。

回看：前面的套路 —— 探索了怎样从三类按角分类的三角形，合情推理。（思维结构图）

【设计意图】: 文化，文化，贴标签式的播放一段关于三角形内角和发现的数学史的文化微课固然方便，但是没有把数学文化的精髓体现出来。张兴华老师曾说：数学和文化之间又具有怎样的关系？数学思想 \ 方法 \ 思考是否属于数学文化的范畴，并且构成数学内在的文化意义？因此，作上面的尝试，让每个孩子重温帕斯卡的发现之路，变实验操作验证为抽象推理验证。同时及时回顾推理的套路。

3.3 号锦囊：套路合情推理。

后来，大家听说这个 12 岁的少年那么能干，都更来劲了。出示小贴士：

从按边分类的三角形，又能不能推理出结论呢？学生仿照锦囊 1 的套路，提出推理方案，如下：

等腰三角形（等边）内角和是 180°。

不等边三角形内角和是 180°。

浓缩成 1 句话：.......

智慧探索出推理结论。锦囊验证。

【设计意图】把按角分类的三角形内角和推理验证的思路，再在按边分类的三角形内角和推理验证过程中重演，建立合情推理（归纳推理）的模型。

（三）巩固练习。（HI-TEACH 方式，IRS 投票或抢答，激趣）

1. 学以致用，智慧投票，快速抢答。学来当居委会大妈，不吵架。

   （1） 微课截图。回答教材主题图：谁个子大谁的内角和就大？投票决定。

（2）三角形分与合，内角和的变化投票。

2. 教材第二题的正方形，引出另一种相反方向的推理套路练习：演绎推理。

          正方形内角和是 360°。
              |

   大胆猜想 （长方形）内角和是 360° | （每个四边形）内角和是 360°

（可以用今天学的三角形内角和 180° 来证明）

三、课堂延伸（线上提交探究）

帕斯卡说：人是为了思考才被创造出来的，不仅仅是因为父母想传宗接代. 这节课你思考了吗？看到 “三角形内角和是 180°”，你还想继续深入思考什么？ 顺向思考 四、五、六...... 外角 逆向思考......

留给大家一个小作业：乐教乐学平台提交研究成果。

7.【课前首学第二稿】

《探索与发现：三角形内角和》课前首学单（第二稿）

                 班级：             姓名：                              
                 

一、认真观看 3.0 微课，再按照微课里的测量方法，把老师给你的三角形，标出内角，用量角器测量出度数，并求和。

三角形的形状 每个内角的度数 三个内角的和

二、观看完微课，微课中的小朋友，他们测量以后计算出来的三角形内角和:

分别是 ()、()、( )、( )、( )。

三、关于三角形的内角和，我发现：

关于三角形的内角和，我还有疑问：

8.【教学设计第三稿】

一、谈话开课。

今天我们将一起探究 ——（齐读：三角形内角和）。

请拿出昨天老师给你的三角形，指一指，它的内角在哪？内角和又是什么？

说到三角形，你会联想到哪个常用的测量工具？（三角板）

PPT. 这里有一副三角板， 说说它们的每个内角是多少度？内角和呢？

三角板刚好是什么形？（三角形），也就是说这个三角形的内角和是多少度？怎么知道的？

从刚才两个三角形的内角和计算中，你发现了什么？

师：那我们能不能就说：左边三角形内角和 180，右边 180, 所有三角形内角和都是 180 度呢？

师：既然有分歧，我们想办法证明自己的观点。/ 预设：这两个三角形就能代表所有三角形了吗？

师：你们准备怎么验证？

师：动手测量是最直接的方法。全世界有那么多三角形，我们都挨着测量完吗？取样？锐角、直角、钝角。

（板书贴三个教具）

二、汇总课前数据，解决疑问。

昨天我发给大家的三角形里面有这些形状的三角形吗？来，汇报一下，你测量的是什么三角形，内角和多少度？ （贴教具，PPT 打勾）

追问：还有谁的是直角三角形？请起立，多少度？/ 有其它形状的三角形吗？多少度？依次处理锐角、钝角三角形。

微课中的小朋友也测量了 5 次，谁来报数据？

观察汇总的内角和数据，你有什么发现？

你还有什么疑问吗？

预设：同样都是三角形，为什么？ / 三角形家族内角和最小？

微课验证误差。

我们发现，直接量方法好，虽然有误差，不准确，但我们能知道三角形的内角和在 180 度左右？究竟是不是所有三角形的内角和一定就是 180° 呢？还有其它不同的方法吗？

提示：180°—— 你会联想到哪个图形？怎样把三个内角变成它呢？

三、操作验证，小组合作。

互学要求

1. 用手中的三角形，独立思考验证方法。有方法后小组内交流。

2. 如果自己没有想法，可以打开小组内的信封，四人小组共同来探索一下。

3. 小组有想法后，作好汇报准备，如果时间充足，可以继续探索其它方法。

教师巡视，指导。

汇报顺序：撕 / 折 / 摆 / 抽样。

方法 1：生：撕拼（）你有疑问吗？方法相同的举手？形状呢？能不能撕拼成平角？其它形状的？谁补充。 你验证的是什么三角形？谁来小结：不论是，都。

方法 2：生：折。有疑问或补充吗？（预设：折来对不齐呀？经验介绍？）你验证

方法 3：摆拼。三个或 6 个，注意推理。重复。

十分会思考，想出了这么多方法，要领是什么？方法有共同之处吗？

带着问题观看微课 2.

微课，方法要领是什么？撕拼、折拼、摆拼，共同之处？

小结：三种方法都不错，但是操作过程中仍然有误差。想想，能不能借助我们学过的常见的图形，不撕、不折、不拼，想办法说明三角形的内角和一定是 180 度。

四、逻辑推理验证

提示：联想 —— 三角形（ ），180 度 —— 平角，还有特殊角度吗？

长方形，能想到方法吗？

生：长方形 —— 对角线，剪成两个完全一样的直角三角形，长方形的四个内角是 360°，其中一个直角三角形的内角就是 180°。

推理方法 —— 验证直角三角形的内角和是 180°，同意吗？这方法严密吧？

介绍帕斯卡 ——12 岁发现，长方形。

你还能用这种严密的推理方法，验证锐角三角形、钝角三角形的内角和是 180° 吗？

这次，就用这两个直角三角形，谁来试试？ 生：合，成一个锐角三角形，也是 180. 生：合，成一个钝角三角形，还是 180°。 归纳：回头看看

不论是测量，还是操作验证，还是推理，我们都验证了哪三类三角形的内角和是 180 度，现在能把这三句话合成一句话吗？（任意或者所有）

回看微课图，解决小三角形的问题，学生先回答。高三角形？胖三角形？小 三角形？发现：不论高矮胖瘦都是 180 度，与大小有关吗？与形状有关吗？ 电脑验证：不死心，验证一下。仔细观察，这个过程中，什么变了，什么没变？

五、练习。

1. 判断：(评价) 猜一猜，这块三角形的碎玻璃可能是（ ）三角形？ 投票 1.2.3

六、课堂小结；收获。联想。还想探索什么呢？

9.【教学设计交流研讨 2 主要观点】

郑大明师父：测量环节必须不能忽视，课中没有？这是最直观的验证方法；要注意录像采集时的各种环节得呈现出来。

代：测量环节我们前置了，放在课前，在家测量。

黄萍：教学语言要精炼，环节之间要注意小结，我来梳理设计稿。

李勇：学生操作的学具不够精致，不够突出，可以制作得更精美一点，我来完成

胥平：学生课前要温习相关的知识，不然容易衔接不上。

王琼：学生课前在家线上学习，完成首学单的照片可以作适当收集。

10.【教学设计最终稿】

学习目标： 1. 通过量、剪、拼、折等直观操作活动，探索并发现三角形内角和等于 180°，发展动手操作、观察比较、逻辑推理的能力。

2. 能运用三角形内角和的性质解决一些简单的实际问题。

3. 在亲历探索发现的过程中，体验数学思考与探究的乐趣，培养学习数学的兴趣。

学习重点：让学生经历知识形成、发展和应用的全过程，并会运用知识解决问题。

学习难点：量角带来的误差；探索验证方法的多样性，尤其是推理验证。

学习准备：3.0 微课片段、PPT、学习单、操作材料包、智慧教室环境。

学习过程：

一、前置学习，课前首学

（一）观看微课 3.0 片段，播放微课到 4 分 30 秒。

（二）完成线下首学单，测量三角形，并计算内角和，填写观看微课测量后的发现和疑问。

【设计意图】基于真实的学情出发，体会测量过程中因为 “误差” 带来的质疑？三角形内角和一定就是 180 度吗？怎么都测不到？既然操作探究得出的实验数据会受到误差的影响，那么还有没有另外的方式避免这样的 “误差” 呢？至于为什么要前置，发现 “测量” 是孩子们能够最先想到的、最普遍想到的方法。同时也发现全国部级一等奖优课，仅仅处理到操作得出结论，后面没有进一步处理到深度推理，时间就不够了，因此，把 “量 + 算” 的环节前置，为后边的操作探究和推理验证留足时间。

二、线下体验，课堂四学

（一）热身：归纳小体验。

归纳：你能把下面的几句话归纳成一句话吗？

热身：我会归纳4.5 班只有三个组；4.5 班一组的同学都是吃货； 4.5 班二组的同学都是吃货；4.5 班三组的同学都是吃货； 得出结论：4.5 班所有同学都是吃货

【设计意图】初步体验归纳推理，为后续体验归纳结论作铺垫。

（二）谈话引入 1. 直入主题：出示课题。

2. 什么是三角形的内角？内角和呢？学生指角，明确三个内角和内角和。

3. 出示一副三角尺：说出每个内角度数，内角和度数。

4. 大胆提出猜想：三角形内角和是 ——180°？能说所有三角形内角和都是 180 度吗？（生：不能）

5. 什么方法验证？预设：撕拼、测量等。

6. 测量方法最直接，所有的三角形都要量吗？（生：有代表性的）

7. 哪些三角形有代表性？（生：直角三角形、锐角三角形、钝角三角形。）（根据学生的回答贴出对应的三角形）这些三角形能代表所有的三角形吗？

【设计意图】多次试教发现孩子们不会指角，不能大胆提出猜想，而且因为受了观看微课后的影响（微课里面测量出 5 个内角和数据），她们便认为微课是 “权威”，从而影响他们填写发现 ——“并不是所有三角形内角和都是 180 度”，只是绝大多数。因此，从特殊三角形出发，引导他们提出完整的猜想。

（三）前置汇报，获取数据。

课前已经完成测量了，汇总大数据。

1. 抽两人说一说自己测量的是什么三角形，它的每一个内角是多少，这个三角形的内角和是多少？

2. 全班用 IRS 反馈器投票，汇总数据。一是测量的三类三角形数据；二是内角和数据。

3. 即时出示：根据大数据生成的全班测量结果统计图。

4. 观察数据，你有何发现？你认为三角形的内角和就是多少？

5. 为什么还有不同的度数呢？

6. 梳理课前大家提出的几个问题，带着问题，观看微课 —— 电脑验证片段。

机动调整 / 预设：（1）三角形内角和跟它的高矮、胖瘦、大小有关吗？（2）三角形的内角和跟它的形状有关吗？（3）......

7. 解决误差和提出的问题。

提出测量，容易产生误差，你还能用别的方法来验证三角形的内角和是 180° 吗？

【设计意图】根据学生前测情况，展示前测真实学情，梳理问题，测量中的 “误差” 的问题为什么会出现？用信息技术手段解释 “误差” 的产生。从而引发学生思考：怎样验证避免出现误差？还有别的方法吗？激发探究的欲望。

（四）动手操作验证

1. 由 180°，你联想到什么？

2. 小组探究，出示互学要求，先独立思考，再小组合作探究信封，作好汇报准备。

信封内容：6 个完全一样的某类三角形；1 个长方形。

3. 小组汇报，预设方法

方法 1：撕拼 —— 总结（ ）三角形的内角和是 180°。

方法 2：摆拼 —— 总结（ ）三角形的内角和是 180°。

方法 3：折拼 —— 总结（ ）三角形的内角和是 180°。

方法 4：长方形分成两个完全一样的直角三角形。（学生是否能出？）

4. 操作验证，得出结论：三角形的内角和是 180°。

5. 沟通方法间的共同之处，撕拼和折拼的要点是什么？

6. 观看微课 3.0 操作方法的片段，梳理方法提示。

【设计意图】：通过分类剪拼、撕拼，用合情推理归纳出结论，在推理的过程中，链接推理的核心关键 —— 把三个内角剪拼、撕拼成的图形是平角，因为平角是 180 度，所以三角形的内角和是 180 度。再根据角进行分类，我们把三角形分成了锐角三角形、钝角三角形和直角三角形，通过选取呈现不同的三角形，由特殊到一般，实现操作推理验证结论。

（五）逻辑推理验证

1. 借助长方形推理，不测量，不操作，我们又能验证三角形的内角和是 180° 吗？（学生思考并操作）

   预设 1：学生如果不能想到，老师提示，联想 360°。

预设 2：长方形内角和 360，把它分成两个完整的直角三角形，每个 180 度。

2. 师生共学，链接帕斯卡：重温 12 岁的天才数学家之路。

3. 已知直角三角形的内角和是 180°，你能用这个结论，推理验证锐角三角形、钝角三角形的内角和也是 180° 吗？

   预设：（师生共学）学生能推理 / 学生不能推理。

4. 回头总结，梳理方法，归纳推理。

【设计意图】: 文化，文化贴标签式的播放一段关于三角形内角和发现的数学史的文化微课固然方便，但是没有把数学文化的精髓体现出来。张兴华老师曾说：数学和文化之间又具有怎样的关系？数学思想、方法、思考是否属于数学文化的范畴，并且构成数学内在的文化意义？因此，作上面的尝试，让每个孩子重温帕斯卡的发现之路，变实验操作验证为抽象推理验证，同时及时回顾归纳推理的套路。

（六）学以致用，即时测评。

 运用结论解决实际问题，选取三道新世纪小学数学配套练习册里面的基本练习题，完成全班保底的基本要求。
 
 形式：选择题，IRS 反馈器完成，即时汇总正确率，了解学情。
 
 填空题：机动。
 

【设计意图】运用智慧教室的即时投票反馈功能，激发孩子的兴趣，掌握学情，为下一步布置课后线上作业提供参考依据。

（七）总结延伸。

通过今天的学习，你有收获吗？你还想要研究什么？

预设：结论、方法等。四边形、五边形、六边形的内角和？三角形的外角……

【设计意图】体现知识点和思考方式的关联结构化，同时也布置线上提交作业，将课堂延伸到课外，让混合式学习成为学生进行课外数学拓展研究的一个重要方式。

板书设计：( 图)

三、课后评价，线上测评。

11.【研讨花絮 1】

12.【研讨花絮 2】

故事导入激发了学生学习的兴趣。教师出示较为简单的图形进行比较，让学生通过观察轻而易举的比较出大小，但是当不太好观察的时候，这种方法就不奏效了，引导学生动手操作，自主实践，让学生体会图形的面积是一个数量概念，与图形边界的形状无关，也与图形边界的长度无关。通过用硬纸板或报纸面积单位的正方形，直观理解面积单位的含义，直接感受面积单位的实际大小。

将 3.0 微课直接用于课堂教学中，是对当下混合式教学模式的一种探究。选择四学模式进行教学也是一种大胆尝试，因为这种教学模式更多的是学生的自主探索、小组交流、全班交流，给予学生更大的成长空间，同时也给了老师更高的挑战，因为教师将如何引导获得所学需要更多的思考。

每一个教学环节都特别注重问题的聚焦，每一个环节的设计意图都非常明确。在首学单上要求学生任意画一个三角形，再量出三角形的内角和，这一点教师很有魄力，没有束手束脚的规定画直角、锐角、钝角三角形中的一种来进行测量，这样的教学生成更有研究意义。其次敢于让学生尝试多种方式来进行验证，培养了学生科学探究的精神。

通过量、剪、拼、折等直观操作活动，探索并发现三角形内角和等于 180°，发展动手操作、观察比较的能力。在亲历探索的过程中，体验数学思考，让学生经历三角形的内角和是 180°，这一知识的形成发展和应用的全过程。发挥了学生的主动性，达到了合作的有效性。

通过量、剪、拼、折等直观操作活动，发展动手操作能力。验证方法的多样性，鼓励学生大胆实验。拓展练习过程中，注重知识、方法、思想的迁移。

@代益梅 做好主题、教材、学情的分析是上好一堂课的基础。充分的了解学生的情况，才能有针对性的设计出适合学生的教学设计。融合了线上线下资源，也是本堂课的一大特色。

@代益梅 学生通过量一量三角形每个角的度数，有的学生得到三角形的内角和正好是 180°，有的大于 180°，而有的则小于 180°，由此让学生去想办法去验证三角形的内角和的度数。在验证的过程中，学生采用了把三角形的三个角撕下来拼成直角的方法、把三角形的三个角折成平角的方法得出了三角形的内角和是 180 度。在整个教学过程中，教师采用了猜想、验证、得出结论、应用的四个探究环节，让学生经历了知识的发生、发展过程，提高了解决问题的能力。这一系列活动潜移默化地向学生渗透了 “转化” 的数学思想，为后继学习奠定了必要的基础。

本节课通过初学，互学，群学，共学，让学生利用已有的知识对内角进行测量并求和，使学生在测量过程中体会数学学习的严谨性，感受测量中的误差对结果的影响。

老师用线上与线下学习相结合的方式，通过量、剪、拼、折等直观操作活动，发展动手操作能力。验证方法的多样性，鼓励学生大胆实验验证。

混合学习可以提供多种学习内容，使不同的学习内容形成互补。学习者既学习结构性强的知识体系，如通过接受实时讲授和学习网络课件，又接触大量信息资源，如通过搜索网络资源，有利于培养他们的终身学习能力，这一点对于成人学习者是至关重要的。混合学习还使学习者一方面获得系统的知识，同时也能接触到最新的发展动态，使学习内容接近领域的发展现状，接近学习者的工作实践环境。学习者经过这样的学习后，可以马上将理论应用于实践，真正实现学以致用。学习内容适应了学习者的需要，就会引发学习者的内在学习动机，实现良好的学习效果。

量、剪、拼、折等直观操作活动，探索并发现三角形内角和等于 180°，发展动手操作、观察比较的能力。在亲历探索的过程中，体验数学思考，让学生经历三角形的内角和是 180°，这一知识的形成发展和应用的全过程。发挥了学生的主动性，达到了合作的有效性。

在教学设计过程中，代老师充分采用 “挖掘教材资源，创造性的应用教材” 这一数学策略。理清教材的内在联系，找准教材的知识脉络，预设出解决教材难点的策略。这节课从学生已有的经验出发，让学生亲身经历 “三角形内角和” 的猜想 - 验证 - 推理 - 小结 - 应用的全过程。为学生提供充分从事数学活动的机会，让他们积极主动地探索，解决数学问题，发现数学规律，获得数学经验。

通过观察、仿写、解释和表述的学习活动，自己发现问题、提出问题，归纳和总结规律，积累合情推理的数学活动经验，提升思维能力。

学生利用已有的知识对内角进行测量并求和，使学生在测量过程中体会数学学习的严谨性，感受测量中的误差对结果的影响。

设计首学任务，让学生自主探索三角形内角和规律。共学时分别呈现三种不同的三角形（直、锐、钝）度数。结合微课揭秘，让学生不被误差困扰。

本节课以学生为主体，充分关注学生的自主探究与合作交流，从设疑导入、自学猜想、实践验证、到最后的展示交流练习拓展，每个环节都由学生探索完成，充分体现了以学生发展为本的教育理念。

教学中，给学生充分的时间和空间去经历摆一摆、画一画、算一算的自主探究活动，不光是获得结论，更应该让学生经历探究过程，培养学生科学的探究态度和初步的探究能力、思维得到发展。

代老师通过让学生摆一摆、画一画、算一算的自主探究活动，充分关注学生的自主探究与合作交流，从设疑导入、自学猜想、实践验证、到最后的展示交流练习拓展，每个环节都由学生探索完成，充分体现了以学生发展为本的教育理念。

@代益梅 一千个三角形会不会有一千个内角和这一问题设置引发学生思考。在语文中千人千面，一千个读者一千个哈姆雷特。学生固有的思维可能会出现理解偏差，此时设置这一疑问，让学生对这句话产生质疑，然后实际动手操作测量，自己提出问题，解决问题，验证问题。充分体现了以学生为主体的教学理念。

这节课，导入直接切入教学主题，从度量不同的三角形内角和入手，再通过量、剪、拼、折等直观操作活动，进行验证，探索并发现三角形内角和等于 180°，发展动手操作、观察比较的能力。能运用三角形内角和的性质试求四边形的内角和，尝试解决一些简单的实际问题，渗透数学文化，体验数学思考与探究的乐趣，培养学习数学的兴趣。

每一个教学环节都特别注重问题的聚焦，每一个环节的设计意图都非常明确。在首学单上要求学生任意画一个三角形，再量出三角形的内角和，这一点教师很有魄力，没有束手束脚的规定画直角、锐角、钝角三角形中的一种来进行测量，这样的教学生成更有研究意义。其次敢于让学生尝试多种方式来进行验证，培养了学生科学探究的精神。

通过量、剪、拼、折等直观操作活动，发展动手操作能力。验证方法的多样性，鼓励学生大胆实验。这节课从学生已有的经验出发，让学生亲身经历 “三角形内角和” 的猜想、验证、推理、小结、应用的全过程。

代老师将 3.0 微课直接用于课堂教学中，是对当下混合式教学模式的一种探究。选择四学模式进行教学也是一种大胆尝试，因为这种教学模式更多的是学生的自主探索、小组交流、全班交流，给予学生更大的成长空间，同时也给了老师更高的挑战，因为教师将如何引导获得所学需要更多的思考。

在教学设计过程中，代老师在认真解读教材的基础上，首先把这节课地位在探索研究课，把准教材的知识脉络，找出解决教材难点的策略。这节课从学生已有的经验出发，让学生亲身经历 “三角形内角和” 的猜想 - 验证 - 推理 - 小结 - 应用的全过程。为学生提供充分从事数学活动的机会，让他们积极主动地探索，解决数学问题，发现数学规律，获得数学经验。老师善于做好学生学习的组织者、引导者和合作者、能关注学生的认知结构和主动参。

通过量、剪、拼、折等直观操作活动，探索并发现三角形内角和等于 180°，发展动手操作、观察比较的能力。在亲历探索的过程中，体验数学思考，让学生经历三角形的内角和是 180°，这一知识的形成发展和应用的全过程。发挥了学生的主动性，达到了合作的有效性。

是的，微课 3.0 让人更加理解何为 “以生为本”。本节课通过实际操作，探索并发现三角形的内角和。学生经历了严谨的数学探索过程，培养了学生科学的研究精神。

教材按照 “创设情境、解决问题、进行验证” 思路进行编排的，老师的设计加入了自己对学情的分析和对教材新的解读，教学环节也做了新的设计，每一个教学环节注重问题的聚焦，设计意图非常明确，学生经历摆一摆、画一画、算一算的探究活动，不光是获得结论，更经历了过程，学生的思维得以发展。

通过量、剪、拼、折等直观操作活动，发展动手操作能力。验证方法的多样性，鼓励学生大胆实验。这节课从学生已有的经验出发，让学生玩中学

代老师的教学设计中用到了 “四学”，“四学” 是什么？它的作用与价值是什么？请代老师介绍一下。谢谢！

本节课代老师通过量、摆、拼等不同方法来验证三角形内角和，有利于学生认识图形 的性质。也可以让学生通过分析三角形内角和的来历深入探索，进而让学生更好的掌握三角形的内和。紧扣 “混合式学习模式实践与探索” 这节课的设计更有创新。

通过量、剪、拼、折等直观操作活动，发展动手操作能力。验证方法的多样性，鼓励学生大胆实验。拓展练习过程中，注重知识、方法、思想的迁移。

代老师的团队思考缜密，呈现内容丰富多样，基于儿童视角重构课堂，值得学习

促进学生深入理解分数的意义，理解度量的内涵和价值。所提供给学生研究的图形也很有针对性。

老师导入上利用微课创设情境，将线上和线下资源相结合，并且进行小组交流，利用集体的智慧解决问题。

微课的作用体现在：三种不同的三角形（直、锐、钝）度数呈现。 聚焦：为什么会产生这样的误差？ 用电脑微课或 PPT 动画方式解决。在实际操作中学生遇到这样的问题，只告诉他误差正常，可以不能让学生真正理解。微课弥补了实际操作的缺陷。

感谢老师的分享，教学设计非常有借鉴意义！

这节课体现让孩子们质疑求证，科学的探究精神

这节课微课很好的做了线下课的补充，而且是必备的。课上的探究操作验证必不可少，微课能包含很多知识量，能很好的融入其中

尊重学生主体地位，更关注数学课的本质内容。本次活动启发了我们要真正做到不仅 “授之以鱼”，更重要的是 “授之以渔”，过程与结果都很重要，我们在课堂教学时，不能只关注学生对于知识点是否掌握，从学生终身发展的长远角度出发，我们更应该关注学生获取知识时的学习过程，教师在教学时要充分给予学生思考、交流的时间和空间。

此课从学生已有的经验出发，为学生提供充分从事数学活动的机会，让他们积极主动地探索，亲身经历 “三角形内角和” 的猜想 - 验证 – 归纳总结的全过程，在观察、仿写、解释和表述的学习活动，发现问题、提出问题、解决问题，积累了数学活动经验，提升思维能力。

学生利用已有的知识对内角进行测量并求和，使学生在测量过程中体会数学学习的严谨性，感受测量中的误差对结果的影响。