本帖最后由 yinhua1982 于 2019-10-14 13:16 编辑
尊敬的各位专家、同行:
大家好!我是来自 <b> 广东省深圳市宝安区孝德学校的殷华 </b>,很高兴与大家在这里认识!今年我非常荣幸能参加新世纪小学数学第十四届基地教学设计与课堂展示 “度量” 主题专场活动。<b> 我参赛的 </b><b> 内容是北师大版四年级上册第一单元第 6 课时《从结绳计数说起》。</b> 本节课是小学阶段认识自然数的最后一个内容,主要是结合十进位值制计数法的形成过程,了解自然数的产生与发展,对自然数的意义与特征进行总结与概括,为后续系统地学习小数和分数奠定基础。在接下来的时间里,我们会以课程标准为指导、认真研读教材、了解学生,争取完成一份适合学生发展的设计。希望能得到各位专家、老师的指点!
导读:(点击链接,快速跳转至相应版块)
[教材图片(2楼)](https://bbs.xsj21.com/forum.php?mod=redirect&goto=findpost&ptid=125729&pid=173177)
[教学设计初稿(3、4楼)](https://bbs.xsj21.com/forum.php?mod=redirect&goto=findpost&ptid=125729&pid=173178)
[9月6日研讨](https://bbs.xsj21.com/forum.php?mod=redirect&goto=findpost&ptid=125729&pid=177012)(7 楼)
[《从结绳计数说起》的选题思考](https://bbs.xsj21.com/forum.php?mod=redirect&goto=findpost&ptid=125729&pid=176933)(6 楼)
[教学设计二稿](https://bbs.xsj21.com/forum.php?mod=redirect&goto=findpost&ptid=125729&pid=177083)(13、14、15 楼)
[9月11日上课照片](https://bbs.xsj21.com/forum.php?mod=redirect&goto=findpost&ptid=125729&pid=177098)(16 楼)
[
本帖最后由 yinhua1982 于 2019-7-21 15:25 编辑
从结绳计数说起
教学内容
从结绳计数说起 (北师大版教材第 12~13 页)
教材简析
本节课是小学阶段认识自然数的最后一个内容,主要是结合十进位值制计数法的形成过程,了解自然数的产生与发展,对自然数的意义与特征进行总结与概括,为后续系统地学习小数和分数奠定基础。
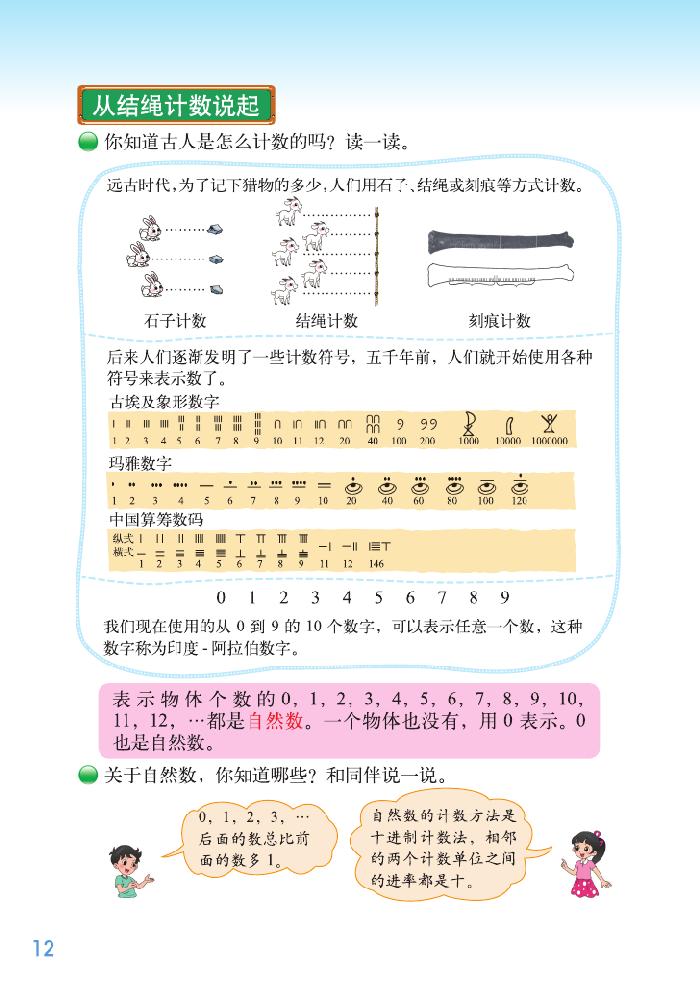
教科书编排了两个问题,第一个问题呈现了数的发展的三个阶段,首先介绍石子计数到结绳计数再到刻痕计数,了解计数方法逐渐由具体到抽象的过程;其次介绍了古埃及象形数字、玛雅数字和中国算筹数码,了解符号表示数逐渐从具体到抽象的过程;最后介绍了用印度 --- 阿拉伯数字表示数。这样的编排目的是让学生从计数和符号两个层面的抽象过程认识自然数。第二个问题是对自然数的特征进行总结和概括。
学情分析
1. 知识层面 : 从入学到现在,学生通过学习数的认识与计算,一直在逐步认识自然数,积累了许多的知识与活动经验,本节课主要是以文字和画图的方式介绍自然数产生于发展的历程,学生能在学习的过程中了解更多的数学史。
2. 技能层面 :通过前三年数学技能的训练,学生的各项能力已经得到了提高,在本课的学习中能对自然数的特征进行总结概括,适合采用阅读、表演、观察、交流的方法,感受历史,总结概括知识。
3. 思维层面 :四年级的学生思维正是从具体形象思维到抽象思维的转变期,他们能够理解本课计数方法发展的 “具体” 到 “抽象” 的过程,也能够理解从 “一一对应” 到 “化繁为简” 的数学思想。
教学目标
1. 使学生感受到数学是在实践过程中产生的,了解计数方法的演算过程,体会其中包含的数学思想。
2. 经历计数方法的演变过程,体会数学一一对应、化繁为简的思想。
3. 感受数学知识与日常生活的密切联系,体会学数学、用数学的乐趣,激发学习知识的热情,渗透数学的文化教育,使学生了解我国古代劳动人民的伟大创举。
教学重难点
重点: 让学生读懂教材中呈现的材料,介绍记数的演变过程。
难点: 密切联系日常生活,感受一一对应与化繁为简的思想。
教学准备
微视频、课件、学生准备的资料。
教学过程
一、视频导入,了解 计数的 起源
师:同学们,你们知道远古时代的人们,是用什么办法来记录自己猎物的多少吗?
学生根据自己的了解,各抒己见。
师:(播放一段视频)为了记下猎物的多少,人们用石子、结绳或刻痕计数,这节课我们就从结绳计数开始了解计数方法的起源与发展。(板书课题 —— 从结绳计数说起)
【设计意图】:使学生感受到数学是在实践过程中产生的,体会数学中一一对应的思想。
二、穿越时空,体会计数的演变
师:以上三种计数方法有什么优缺点?
学生根据生活经验参与小组讨论,并派代表发言,言之有理即可。
师:随着捕猎工具的改进,猎物数量越来越多,一个石子对应一只猎物的计数方法,很难适应计数的需要。同学们猜猜看,超过十的数,该怎么表示呢?
预设学生:用大一点的石头、大一点的绳结、粗一点的刻度来表示十。
师:十进制起源于古人用双手十指计数的方法,成语 “屈指可数” 就是这样来的。但超过十的数,双手的手指用完时,就在地上搁一块石头或一根树枝代表十个,让手指伸直再数。经过长期实践和总结经验,就产生了十进制。
【设计意图】:从 “一一对应” 演变成 “按群计数”,让学生体会数学中化繁为简的思想,也是进位制的雏形。
三、阅读仿写,感受计数符号的必要
组织学生阅读关于古埃及象形数字、玛雅数字、中国算筹数码的材料,再现不同地区和国家的劳动人民的智慧,按照要求对这些计数符号进行仿写。
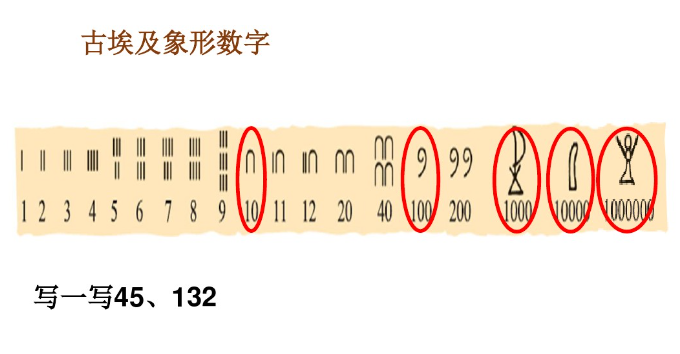
1. 古埃及象形数字(体会进位制思想)
8973
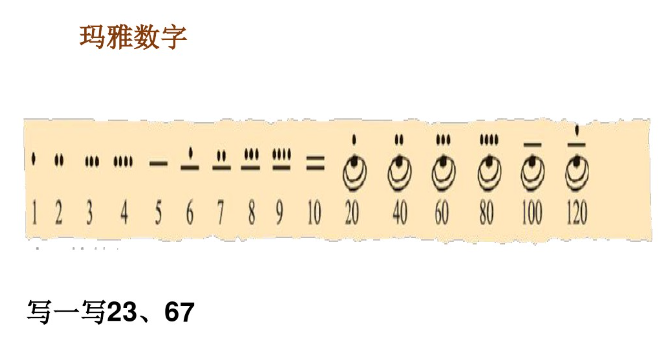
2. 玛雅数字(体会 20 进制思想)
8974
3. 中国算筹数码(体会位值制思想)
8975
【设计意图】:使学生体会到古埃及象形数字只有 “十进” 关系,玛雅数字是 20 进位制,中国算筹数码不仅有 “十进” 关系,还有 “位值” 思想,计数简单明了。
图片:

本帖最后由 yinhua1982 于 2019-7-21 15:19 编辑
四、联系实际,学习自然数和十进制的应用
师:所有的这些数字符号虽然在表示的形式上不同,确是人类文明发展的见证之一。最后,古印度人发明了我们现在使用的印度 - 阿拉伯数字,从 0-9 的七个数字可以表示任意一个数,给我们生活带来很大的便利!
例如,一个物体用 1 表示,两个物体用 2 表示,什么物体也没有就用 0 表示。像这些表示物体的 0,1,2,3,4,5,6,7,8,9,10,11,12,13...... 都是自然数。
师:关于自然数,你知道什么?或者你想知道什么?
预设:学生 1:最小的自然数是 0。
学生 2:没有最大的自然数。
学生 3:后一个自然数总比前一个自然数多 1。
学生 4:自然数的排列有一定的顺序。
学生 5:自然数满十进一。
教师小结:同学们,计数方式,十进制,自然数等等这些与我们的生活息息相关,你们学了这节课,就可以带着数学的眼光,在生活中留心观察,还有哪些不同的进制,我们下节课可以一起分享哦。
【设计意图】:通过对学生介绍印度 — 阿拉伯数字的由来,激发学生学习数学的兴趣,又开阔了学生的视野。师生共同总结出自然数的无限性、有序性及十进制计数法。
五、课末巩固,学以致用
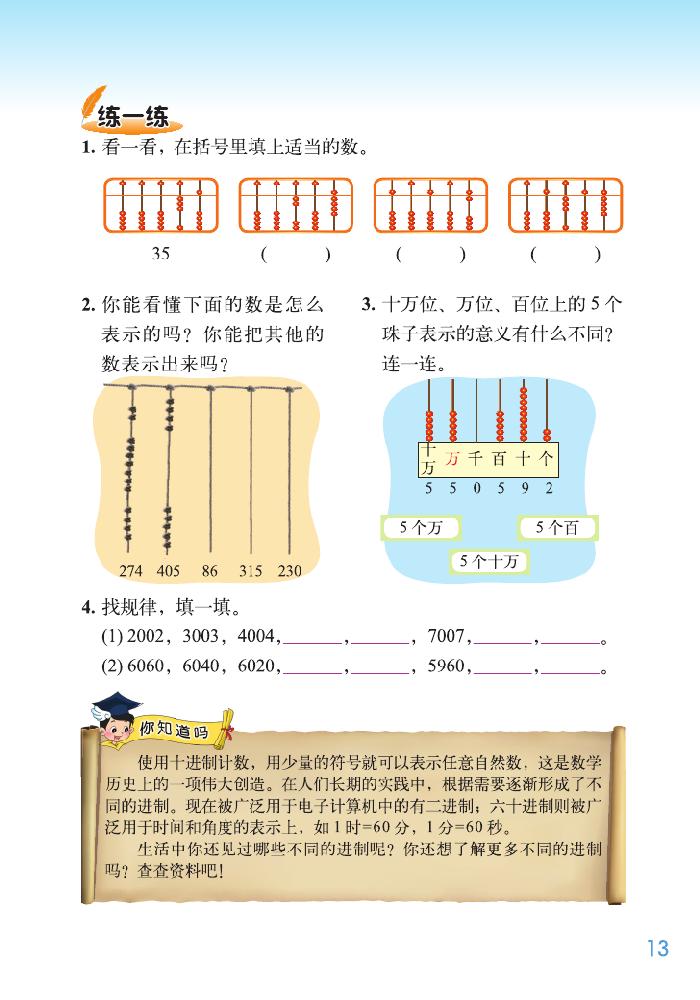
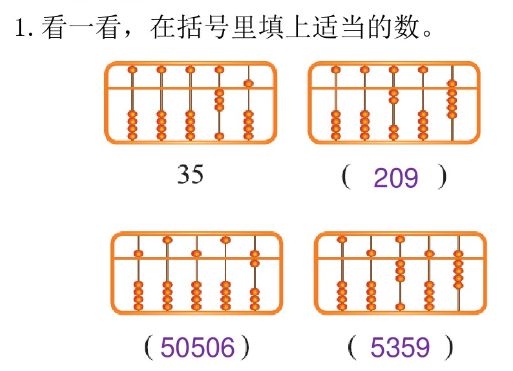
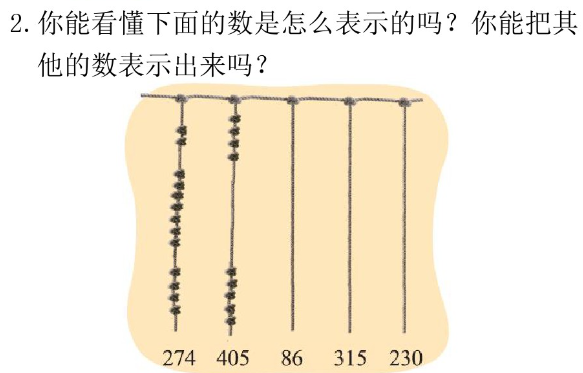
1. 教材 “练一练” 第 1、2 题, 目的是训练孩子对不同计数方法的认识和运用。很有代表性。让孩子们做一做,说一说,听一听。
8976
8977
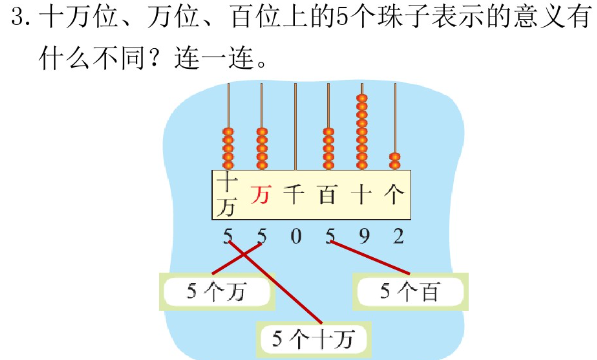
2. 教材 “练一练” 第 3 题, 让孩子们体会到,相同的数在不同数位上表示不同的意思。
8979
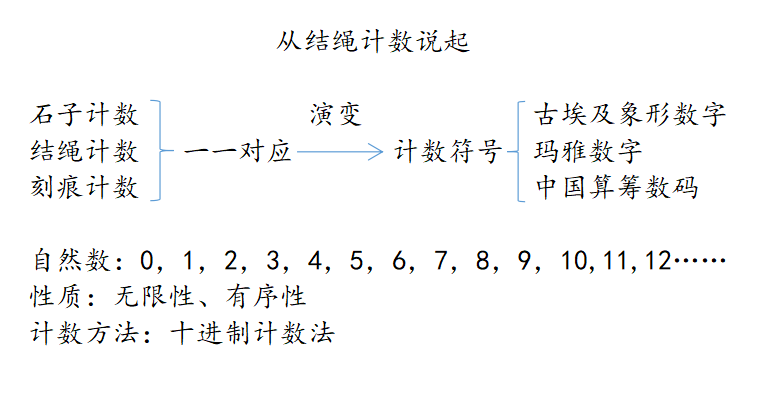
3. 教材 “练一练” 第 4 题找规律, 对应的是自然数的认识,锻炼孩子的数感。
8980板书设计
8981
图片:

本帖最后由 yinhua1982 于 2019-9-17 14:54 编辑
《从结绳计数说起》的选题思考
关于为何要选择《从结绳计数说起》这节课进行打磨与研究,我们团队经过集体讨论后,有以下几点思考:
思考一:关于数量度量的内涵阐述。
史宁中教授认为,度量的本质在于表现事物某些指标的顺序,主要包括两类,一类是通过抽象得到的,是人思维的结果;另一类是借助工具得到的,是人实践的结果。
《从结绳计数说起》这节课介绍的是通过抽象得到的度量,其本质是度量数量的多与少,这个抽象过程依赖于学生对数量多少感知的本能,而抽象的结果,在形式上是舍弃了度量单位的称谓,舍弃了事物的一切物理属性。
思考二:关于数量度量的发展过程。
从石子计数到结绳计数再到刻痕计数,我们不难发现通过 “对应” 来认识和理解事物的数量关系是最原始的、也是最有效的方法。如,将 3 个苹果、4 个梨分别对应绳上的三个结和四个结是从感性具体上升到感性一般的思维过程,是数学抽象的第一步,目的是舍去苹果、梨的物理属性,仅保留事物的数量。
度量是人们认识数学,进而认识现实世界的基本工具和表达语言。度量单位的确立是为了人们能够对度量进行统一的表达和无歧义的交流,因此度量单位必须能够揭示度量的本质,其形成大体都经历了从多元到统一,从粗糙到精细的过程,这是为了日常生活的表达和科学研究的需要。无论是古埃及象形数字、玛雅数字、中国算筹数码还是阿拉伯数字,都是在对应的基础上,尝试用符号来表达数量。如,用符号 3 表示三个结,符号 4 表示四个结,把量之间的多少关系转化为数之间的大小关系,可以让学生感知符号表达是具有一般性的。这是从感性一般上升到理性具体的思维过程,实现了更高层次的数学抽象。
思考三:关于数量度量本质的解读。
最后,让学生逐渐感悟抽象度量的本质:自然数是一个一个大起来的,其中的 1 就是度量单位,那么 5 就是 5 个 1,50 就是 50 个 1。在一般意义上,我们可以把数位个、十、百、千、万等也看作度量单位。如,把 5000 看作 5 个 1000,把 0.05 看作 5 个 0.01 等。
通过合适的教学情境,让学生经历从感性具体上升到感性一般,从感性一般上升到理性具体的思维过 程,体验什么是抽象度量和数学抽象的层次性,培养学生的符号意识,形成数学抽象的核心素养。
本帖最后由 yinhua1982 于 2019-9-17 14:55 编辑
追本溯源,聚焦数量度量发展全过程
---《从结绳计数说起》教学案例与分析
教学内容
北师大版教材四年级上册第 12--13 页
教材简析
本节课是小学阶段认识自然数的最后一个内容,主要是结合十进位值制计数法的形成过程,了解自然数的产生与发展,对自然数的意义与特征进行总结与概括,为后续系统地学习小数和分数奠定基础。 教科书编排了两个问题,第一个问题呈现了数的发展的三个阶段,首先介绍石子计数到结绳计数再到刻痕计数,了解计数方法逐渐由具体到抽象的过程;其次介绍了古埃及象形数字、玛雅数字和中国算筹数码,了解符号表示数逐渐从具体到抽象的过程;最后介绍了用印度 --- 阿拉伯数字表示数。这样的编排目的是让学生从计数和符号两个层面的抽象过程认识自然数。第二个问题是对自然数的特征进行总结和概括。
教学思路
本节课介绍的是通过抽象得到的度量,其本质是度量数量的多与少。为了让学生更好地感受数量度量的本质,笔者在教学中的思路是:
1. 教学中学生学习古人计数的三种方法,感受 “满十进一”、“计数单位”、“计数器” 的萌芽与雏形;
2. 学生自主学习计数符号,体会数量度量的演变过程,感受阿拉伯数字的优越性;
3. 学生总结自然数的特点时,感悟数量度量的本质。
本帖最后由 yinhua1982 于 2019-9-15 17:30 编辑
教学目标
1. 通过观察与操作,感受计数在实践中产生,了解计数方法的演变过程,进一步体会数量度量的发展。
2. 通过阅读与交流,进一步认识自然数,了解自然数的特征。
3. 感受数学知识与日常生活的密切联系,体会学数学、用数学的乐趣,渗透数学的文化教育,使学生了解我国古代劳动人民的伟大创举。
教学重难点
重点: 让学生读懂教材中呈现的材料,介绍记数的演变过程。
难点: 计数方法从具体到直观的过程中,感受数量度量的萌芽与发展。
教学准备
课件、学生准备的材料。
教学过程
一、复习与对比,激发学生对远古计数方法的兴趣。
师:大家有没有看今年的《开学第一课》,其中有一段嫦娥 4 号探测器和玉兔 2 号会面的节目,他俩在月球上碰面,嫦娥还给玉兔拍了很多照片。
师:你们知道地球到月球的距离有多远吗?
师:月球和地球的平均距离为 384000km,谁来给大家念一念这个大数。闭上眼睛想象一下,这么长的距离用一个 6 位数轻易的表示了出来。可见人类智慧的伟大。
师:跨越历史的长河,我们穿越回距离现在几万年的远古时代,那时候没有人造卫星、飞机火箭。人们为了生存群居在一起生活。他们又是怎样计数的呢?你们有了解过吗?(学生回答:石子计数、结绳计数、刻痕划道计数等)
师:今天这节课,我们就从古人的结绳计数说起,了解计数的演变过程。(揭示课题)
【设计意图:播放嫦娥 4 号探测器和玉兔 2 号会面的视频,引出地球到月球的直线距离,让学生感受到大数的广泛应用。继而追溯到没有数字的远古时代,人们又是怎样计数的呢?这样的导入既是对前面所学知识的复习,又能让学生加深对现代数字发展与远古时代计数的强烈对比,激发求知欲望。】
二 、 实践与操作 ,学生 从古人 计数 的演变中感悟数量度量的本质。
1、石子计数:实物的 “一一对应”,了解度量的最初萌芽。
师:一年级我们已经学习过古人用石子计数的方法,比如数羊时,古人怎样记录羊的数量?
生:一个石头表示一只羊。
师:那两只羊怎样表示,3 只呢?11 只呢?
生:换个大一点的石头。一块大石头表示 10,一块小石头表示 1。
师:好主意!这样的计数方法有点像我们的十进制计数法,以一当十、满十进一。
【设计意图:石子计数是远古时代人类最初的计数方法,此环节的设计,让学生感悟 “度量” 的最初需要,这时候已经产生了 “一一对应”、“十进制” 等最初的萌芽。】
2、结绳计数:从石子抽象出 “一个点”,感悟最初的度量单位。
师:随着捕猎工具的改进和捕猎经验的增加,捕捉猎物的数量也不断增加。这时候再用石子计数的方法已经满足不了计数的需要。因此,人类逐步出现了以一个绳结表示一只猎物的启蒙思想,利用绳子打结的方法来计数。也就是我们所说的结绳计数法。
师:老师给每一组同学准备了一根绳子,请你们用绳子打结的方式,表示出羊的数量。(课件呈现羊群图片)
羊的数量为 134 只,学生在合作交流中,研究出利用不同的打结方法表示这个数。
生 1:羊的数量比较大,用一个绳结表示一只羊肯定不行,我们可以用一个小结表示一个、用一个中结表示十个、用一个大结表示一百个。
生 2:我们也可以在最上端打一个结表示 100,在中间打三个结表示 30,在最下面打四个结表示 4。
......
师:同学们的方法都很不错,当时的古人可能没有你们那么聪明能研究出这么多计数方法。但有一点肯定和你们一样,当出现很大的数量时,用一个绳结表示一个数过于麻烦,他们就会想办法,可能是一个大结表示一个百、一个中结表示一个十、一个小结表示一个一。这个有点像我们现在所学的计数单位。
师:看来,那个时候也有了计数单位的萌芽。
【设计意图:此环节让学生操作打结计数,一是让他们了解古人计数方法的提升与飞跃;二是体会到十进位值制的重大价值,经历对数学思想的体悟过程。三是感悟当时计数单位 “一”、“十” 的萌芽。】
3、刻痕计数: 设置合适的单位长度, 从 “一个点” 形成 “一把尺”,丰富了度量的内涵。
师:你们认识这种计数方法吗?(刻痕计数)
师:刻痕计数,就是在木头、兽骨、石块上留下刻痕,通过刻痕来记录数字。
师:这是 1937 年在维斯托尼斯(现捷克共和国南部的摩拉维亚)发现的一根 40 万年前的幼狼前肢骨,7 英寸长(约 17 厘米),上面有 55 道很深的刻痕。从这根骨头上,你有什么发现?
9796
生 1:有短竖线、有长竖线;每条竖线的距离都是一样的。
生 2:有短的表示一,长的表示十。
生 3:像一把尺子。
师:确实像一把尺子,也像我们现在学习的数线图(数轴)。有科学家发现,这些刻痕里藏着非常复杂的计数方法,并非是十进制,甚至还隐藏着乘法和除法的运算。有兴趣的同学可以课后和小伙伴们一起查找资料继续研究。
师:刻痕计数的出现,证明人类对数已经有了更为先进的度量。它不仅扩充了数系,也为人类度量长度做好了准备。
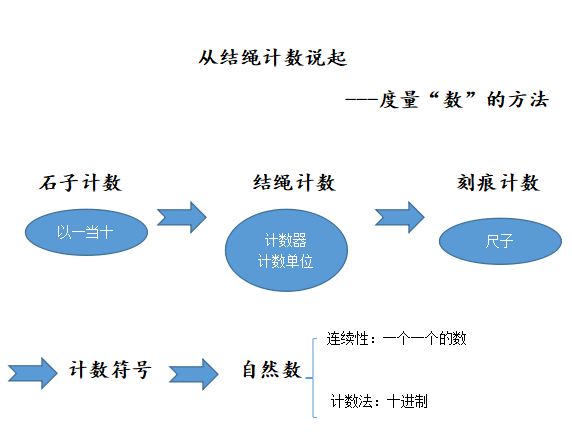
小结:俗话说 “数从数来”,古人最初利用简单的石子计数,再到抽象的结绳计数,最后是刻痕计数。远古时代的人们因为要数的数量越来越多,才在劳动中不断的创造出先进的度量 “数” 的方法.
file:///C:\Users\ADMINI~1\AppData\Local\Temp\ksohtml8112\wps2.pngfile:///C:\Users\ADMINI~1\AppData\Local\Temp\ksohtml8112\wps3.png(课件播放:石头 结绳 刻痕 度量 “数” 的方法 )
【设计意图:远古时代人类三种计数方法的教学,让学生感受计数方法的历史发展,了解一定的数学史。并从计数方法的抽象过程中,体会数量度量的本质:度量数量的多与少。】
图片:

本帖最后由 yinhua1982 于 2019-9-17 14:51 编辑
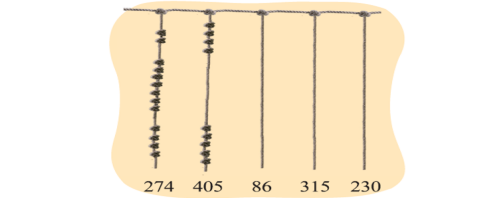
4、拓展练习:感悟最初的 “位值” 思想,使计数简单明了。
9799
教师引导学生完成此题,让学生了解最高位上的 2 个结表示 200,中间的 7 个结表示 70,最下面的 4 个结表示 4。并通过动画演示,将这幅图中的 274 用计数器的形式呈现,进一步感受度量 “数” 的方法。
三、 阅读与讨论,学生 了解五千年前计数方法的演变和发展 , 感受不同国家不同的度量方式。
师:随着人类慢慢地进化,变得越来越聪明,到了五千年前,不同的国家对数量的度量都有自己的方式。
师:请大家仔细读一读书本第 12 页的内容,你能知道哪些信息?把你的发现、想法和你的同桌说一说吧!
学生开始自主阅读,再与同桌交流后汇报。
1、古埃及象形数字
2、玛雅数字
3、中国算筹数码
【设计意图:此环节主要是让学生通过自主学习、合作交流的方式,感受计数符号的发展历史,了解每种数字的特征及不同的进位制,为学习自然数做铺垫。】
四、观察与比较,了解自然数的演变过程,体会其优越性。
1、了解阿拉伯数字的由来。
师:刚刚我们了解了五千年前人们的三种不同的数字符号,和我们现在使用的数字比起来有什么感觉?
生:好复杂哦,我们现在使用的数字简单多了。
师:我们现在使用的 0-9 这些数字叫什么数字?
生:阿拉伯数字
师:阿拉伯数字真的是阿拉伯人发明的吗?
生:是印度人发明的。
师:我们一起来读一读课本的这句话。
生齐读:我们现在使用的从 0 到 9 的 10 个数字,可以表示任意一个数,这种数字称为印度 - 阿拉伯数字。
师:这 10 个数字是印度人发明,由阿拉伯人传播出去的,所以大家都叫它们印度 - 阿拉伯数字。为什么说这是个数字可以表示任意一个数呢?
生 1:因为可以把这些数字组合起来用。
生 2:因为同样的数字摆放在不同的数位上可以表示不同大小的数啊。
2、 认识自然数,了解自然数的特点 。
师:同学们,其实刚刚我们研究的数都可以称为自然数,什么是自然数呢?
生读:表示物体个数的 0,1,2,3,4,5,6,7,8,9,10,11,12,… 都是自然数。一个物体也没有,用 0 表示,0 也是自然数。
师:你知道自然数的特点吗?请和你的同桌说一说你的发现。
生 1: 连续每次加 1;
生 2:后面一个数比前面一个数多 1;
师:我们也可以说相邻的两个自然数相差 1;
生 1:自然数是数不清的,没有最大的;
生 2:10 个一是十,10 个十是百,10 个百是千,自然数也是十进制的,
师:对的,自然数是无限的,自然数的计数方法是十进制计数方法,相邻的两个计数单位间的进率是十。
师:这节课,同学们的观察真仔细,发现的规律真多,了不起啊!
五、巩固与应用,学生加深对所学知识的了解。
完成课本第 13 页中的习题。
结语:
师:人类对计数方法的探索一直都未停止,随着科技的发展,人们对数字的需求越来越庞大。大到外太空的探索、小到微观世界的研究,需要我们创造更多的度量单位来满足。希望大家能学好数学,利用数字发现更多的未知世界。
板书
9800
图片:
殷华老师从具体情境入手,让学生在情境图中自主体会古代人们的计数方法,经历计数方法的演变过程,体会数学一一对应、化繁为简的思想,特别是板书的设计对于体会实物与数字之间 “一一对应” 联系有着明显的视觉感知。
感谢老师的分享,从石子计数到结绳计数再到刻痕计数,我们不难发现通过 “对应” 来认识和理解事物的数量关系是最原始的、也是最有效的方法。如,将 3 个苹果、4 个梨分别对应绳上的三个结和四个结是从感性具体上升到感性一般的思维过程,是数学抽象的第一步,目的是舍去苹果、梨的物理属性,仅保留事物的数量。
本节课根据学生实际学情,通过介绍古代人们如何计数,如何逐步发明、使用各种计数符号等,直观形象的使学生对数的产生有一个初步的认识,并结合学生以往对数的认识,总结概括自然数的意义与特征,感受十进位值制的重大价值,激发学生热爱数学的情感。(许可)我仔细阅读了老师的设计,特别在仿写过程中,用计数单位来数数、用计数符号表示数,能够帮助学生建立符号意识和数感,能否在数字 10 这里让孩子感悟人类发明的伟大,数字 10 是用 1 和 0 组成的,而没有创造出新的符号。
毕金明:度量是人们认识数学,进而认识现实世界的基本工具和表达语言。度量单位的确立是为了人们能够对度量进行统一的表达和无歧义的交流,因此度量单位必须能够揭示度量的本质,其形成大体都经历了从多元到统一,从粗糙到精细的过程,这是为了日常生活的表达和科学研究的需要。无论是古埃及象形数字、玛雅数字、中国算筹数码还是阿拉伯数字,都是在对应的基础上,尝试用符号来表达数量。如,用符号 3 表示三个结,符号 4 表示四个结,把量之间的多少关系转化为数之间的大小关系,可以让学生感知符号表达是具有一般性的。这是从感性一般上升到理性具体的思维过程,实现了更高层次的数学抽象。
殷老师从具体情景入手,并且通过活动,使学生体会到古埃及象形数字只有 “十进” 关系,玛雅数字是 20 进位制,中国算筹数码不仅有 “十进” 关系,还有 “位值” 思想,计数简单明了。