山那边1980

【学生活动照片】

【教学设计（三）】

【教材简析】

本课内容是在学生已经初步理解了体积和容积的意义、掌握了长方体和正方体体积计算方法的基础上学习的，长方体和正方体体积计算方法 “底面积 × 高” 对探索圆柱的体积计算方法有正迁移作用。本课的重点在于引导学生经历 “猜想与验证” 的探索过程，在探索中理解、掌握圆柱体积的计算方法，教材充分利用学生学过的知识作铺垫，采用迁移法，引导学生将圆柱体转化成已学过的立体图形，再通过观察、比较找两个图形之间的关系，可推导出圆柱的体积计算公式。

【教学目标】

1．通过具体情境观察、实物感知、实践操作等活动，感受物体体积的大小、发展学生体积量感。

2．通过圆柱与长方体的 “类比”，经历 “猜想与验证” 探索圆柱体积计算方法的过程，体会 “类比” 的数学思想方法。

3. 会计算圆柱形物体的体积和容积，运用公式解决简单的问题。

【教学重点】圆柱的体积计算。

【教学难点】圆柱的体积公式的推导过程。

【教具准备】圆柱的体积公式演示教具，多媒体课件

【教学过程】

一、首次感知，唤醒量感意识

1. 出示问题，揭示意义

（1）出示图片，提出问题。

师：同学们，圆柱形物体在生活中随处可见，圆柱形的柱子，黄瓜，杯子，饮料瓶...... 下面的问题都和圆柱的什么有关呢？

生：和体积有关。

（2）师生对话，揭示意义。

师：其实求圆柱形物体的大小、圆柱形容器容纳物体的多少，都是求圆柱的体积。那什么是圆柱的体积呢？

生 1：圆柱所占空间的大小就是圆柱的体积

师：这节课我们就一起来研究圆柱的体积。（板书课题：圆柱的体积）

（设计意图：数学来源于现实生活，又应用于生活。《数学课程标准》强调数学与现实生活的联系，选择与学生生活密切联系的问题情境有利于激发学生兴趣，点燃探索新知的热情。）

2. 比较体积，产生量的需要

（1）估计体积 发现量的缺失 （老师准备 60ml 的饮料）

师：每个小组桌面上有一个像这样的圆柱形杯子，装了相同多的水，水是什么形状的？观察一下，根据生活经验估一估这杯水的体积是多少？

生 1：30ml

生 2：100ml

生 3：80ml

......

师：同学们估计的结果相差比较大啊，现在老师给大家提供一个标准，这个瓶子里水的体积大约 180ml 左右，现在你们再来估一估呢。

生 1：80ml

生 2：70ml

生 3：60ml

......

（2）测量体积 感受 60cm³ 的量。（慧道平台展示测量过程）

师：那饮料的体积到底是多少呢？你有什么办法准确得到？

方法一：倒入量杯量直接测量。

师：老师这里正好有一个量杯，你来测量一下，其他同学也一起观察。

方法二：倒入长方体容器中，测量出长宽高计算体积（间接测量）。

师：老师这里还有一个长方体盒子，你能借助它来测量吗？（这个长方体的底面积是 80 平方厘米）

师：通过量杯直接测量和倒入长方体量出数据计算，都可以得到水的体积。

（3）以体积单位度量圆柱，激发 “量” 的矛盾。

师： 60ml 也就是 60cm³。老师为大家准备了 60 个体积为为 1cm³ 的小正方体，它们的体积之和就是 60 cm³，请你装进和老师同样的杯子里，然后摇一摇。与另一个杯中的水比较，你有什么发现？

生 1：60cm³ 的小正方体装进杯子后，看起来比水高一些。

生 2：因为中间有空隙，所以看起来更高了。

师：60cm³ 的水和 60cm³ 的小方块所占空间是一样大的，但装进杯子里以后，水之间没有空隙，但小正方体之间以及小正方体与水杯壁之间都有很多空隙，水无形，小正方体有形，所以要想直接借助小正方体来得出圆柱的体积就比较困难。那这些小方块对于我们研究圆柱的体积会有帮助吗？接下来看我们能否找到它们之间的联系。

（4）链接生活 激化矛盾（接力棒）。

师：水可以借助量杯测量体积，老师这里有一根接力棒，我们想知道这根接力棒的体积，该怎么办？

生 1：溢水法。

生 2：测量出数据。

生 3：转化。

......

师：同学们想的办法其实都可行，那圆柱的体积可能与它的什么有关呢？

生：底面积和高

师：是这样的吗？在接下来的活动中，我们一起来找找答案。

（设计意图：学生对体积量感经验是有些缺失的，借助已有的经验，很难正确的进行估计。学生出现不同估算结果后，再给学生一个参考标准，学生估计的结果就比较接近实际结果了。然后再通过实际量，与之前估的结果对比，可以再次对学生体积量感的经验进行修正，再通过摆 60 个小正方体的活动，进一步巩固学生体积量感。学生想到测量水的体积的方法非常好，但这些方法都具有局限性，求接力棒的体积就不能用到刚才的方法，这时让学生试着想想圆柱的体积与它的什么有关？这时学生会自动唤醒已有知识经验，将影响体积大小的因素指向到底面积和高上来，为后续的学习做好了铺垫。）

二、叠加实物，领悟（体积）量的要素

1. 互学：组内操作（叠） 初步感知体积与底面积和高有关

要求：

（1）叠一叠：将纸片（硬币）一片一片往上叠。

（2）叠的过程：边叠边观察，你有什么发现？

（3）叠好后：对比观察，你又有什么发现？

2. 群学：小组分享（说），逐步明确体积与底面积和高的关系

师：谁来说说你们小组的发现？（慧道平台展示）

生 1：我发现一张纸片很薄，一张的厚度可以忽略不计，当很多张纸片叠在一起时就有了厚度，就得到了一个近似的圆柱。

生 2：在往上叠的过程中，高度在增加，体积也在增加，说明圆柱的体积与高有关。

生 3：我们组叠的硬币和纸片的高度差不多，但纸片的体积比硬币的体积大得多，说明圆柱的体积与底面积有关。

师：通过刚才的活动，我们发现圆柱的体积与底面积和高有关。

3. 共学：组间对比（辨），进一步明确体积与底面积和高的关系

师：同学们说得真好，现在老师把 4 个组的圆片放在一起，硬币放在一起，你又有什么发现？

生 1：观察 4 个组的纸片发现，底面相同，高度决定圆柱的大小。

生 2：高度相同，底面决定圆柱的大小。

师：通过刚才的活动，我们发现圆柱的体积与底面积和高有关。

4. 链接生活，强化量感经验

请你快速判断下面图中两个圆柱的大小。

（设计意图：动手操作是学生获得量感的重要途径，首学和互学环节通过叠纸片和硬币的活动，不仅能感知形成的圆柱是圆形纸片面的叠加，还能感知圆柱的体积与底面积和高有关。群学环节通过组内对比，体会圆柱底面相等，高可用决定体积大小，高相等，底面大小可用决定体积大小，加深了对体积与底面积和高的关系的体会。再通过生活中几组圆柱体积大小的对比，在巩固知识中丰富圆柱体积量感的经验）

三、操作验证，推导体积公式

1. 观看微课，启发思维

师：圆柱的体积到底该怎样计算呢？猜一猜。

生：之前学习过的长方体和正方体的体积用 “底面积 X 高” 来计算，我猜圆柱的体积也是用 “底面积 X 高” 来计算？

师：老师为大家准备了一个微课（圆面积推导过程），一起来看看。

师：转化真奇妙，我们能把一个圆采用化曲为直、化圆为方的方法推导出了圆面积的计算公式。这个过程对你有什么启示？

生 1：不能直接求时可以尝试转化。

生 2：可以将圆柱转化成长方体。

（设计意图：借助微课，将圆面积公式推导过程的再现，为实现经验和方法的迁移做铺垫，也让学生感受到知识内在的统一。）

2. 动手操作，沟通联系

（1）互学：将圆柱 “切拼” 成近似的长方体。

要求：

①操作：将圆柱转化成已学过的近似长方体。

②思考：转化后的长方体与圆柱有什么关系？

③交流：转化后的长方体与圆柱的对应关系。在对应的地方标一标。

④讲解：你是如何推导圆柱体积计算公式的。

（2）群学：交流对应关系，推导体积公式。

师：刚才老师录制了一个小组操作过程的视频，我们先来看一看。（慧道平台录制视频）

师：谁来把你们小组的学习成果与大家分享？（慧道平台呈现学生汇报过程）

生 1：我们小组将圆柱平均分成 8 份，拼成一个近似的长方体，转化后的长方体与圆柱的体积相等，长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高，长方体的体积 = 长方体的底面积乘高，所以圆柱体积 = 圆柱的底面积乘高。

生 2：我们小组将圆柱平均分成 16 份，拼成一个近似的长方体……

（3）共学：对比观察，拓展思维。

师：将平均分成 16 份拼成的长方体与刚才的长方体对比，你又发现了什么？

生：平均分成 16 份拼成的图形更像长方体。

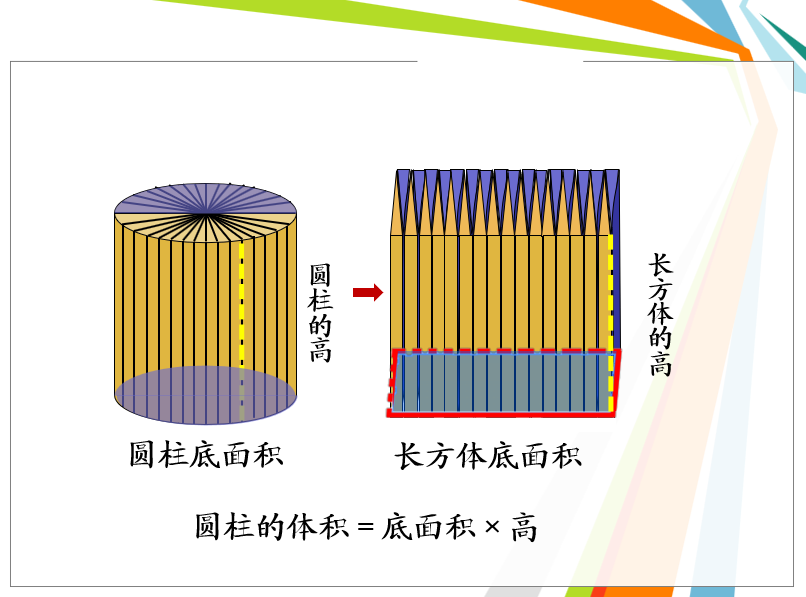
师：如果我们将圆柱底面等分成 32 份，64 份，甚至更多，然后再拼起来会是什么情况呢？（课件演示）

生：分的份数越多，拼成的立体图形越接近长方体。

师：平均分成 32 份，操作起来比较困难，我们借助课件来看看。圆柱通过切拼，转化成近似的长方体。长方体的体积等于圆柱的体积，长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高。因为长方体的体积等于底面积乘以高，所以，圆柱的体积 = 底面积 × 高。用字母表示：V=Sh。(板书二级板书对应：V=πrXrXh)

师：你能像老师这样说一说这个过程吗？说给同桌听一听。

3. 估计体积，发展量感

（1）互学：摆一摆，估计体积，积累量感经验。

师：我们把圆柱转化成了长方体，借助小方块估一估，这个圆柱的体积大约是多少呢？（学生摆一摆，估一估）

（2）群学：看一看，沟通联系，强化量感经验。

（教师播放小组操作过程视频）

师：看，当圆柱转化成长方体后，我们就可以借助小方块来度量了，长方体的长就是圆柱底面周长的一半，决定了方块一排有几个，长方体的宽就是圆柱的半径，决定了方块有几排，长方体的高是圆柱的高，决定了方块有几层。

3. 回顾梳理，建构计算模型

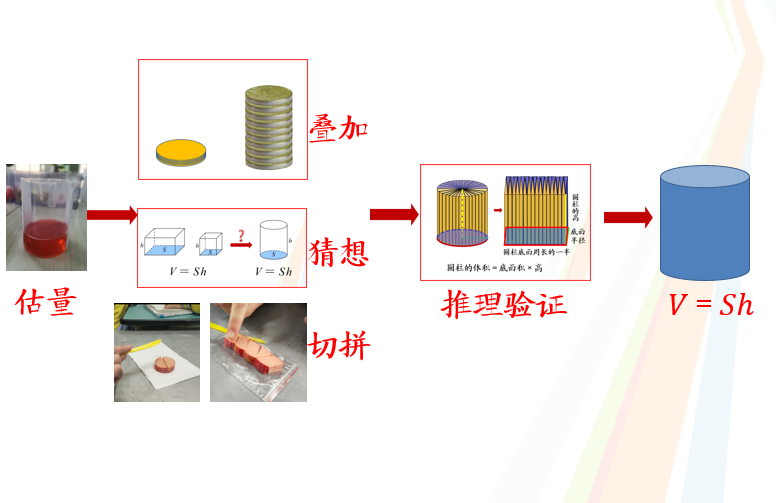
师：刚才，我们通过估一估、量一量等活动，直观感知了圆柱体积的大小。再通过叠一叠、比一比等活动，知道了圆柱体积与底面积和高有关，根据长方体体积公式猜想圆柱体积等于底面积乘高，之后在切一切、拼一拼等活动中，将圆柱转化成了长方体，最后根据等积变形推导出圆柱体积计算公式：V=Sh。其实很多数学研究的发现都经历了这样的研究过程，从现实问题出发，引发猜想，再通过实验验证，从而得出结论。

（设计意图：量感的培养需要丰富的活动经验。通过播放圆面积推导视频，唤醒学习经验，通过回顾长方体、正方体体积计算公式，唤醒体积量感的敏感以及对量的直接反应，学生很容易得出 “圆柱体积 = 底面积 × 高” 的猜想。学生经历将圆柱转化成长方体的过程，更容易理解转化前后 “量” 之间的变与不变，感受量变背后的内在联系。在学生充分操作、交流的基础上再通过观看课件，调动学生多种感官参与圆柱体积公式推导过程，在观察中理解，在比较中讨论归纳，让极限思维、转化思想有机的渗透在课堂教学中。）

四、运用公式，解决问题，固化量感

1. 下面的问题是求什么？

2. 估一估（教师操作，打包纸片，建立新标准，提供 “估” 的方法）

（1）老师手中纸片的体积大约是（ ）立方厘米。

（2）估一估老师手中饮料瓶中饮料的体积是（ ）立方厘米。

师小结：估算时，选择一个适合的参考标准，可以让我们估得更准确。

3. 求下面圆柱体的体积。(单位：厘米)

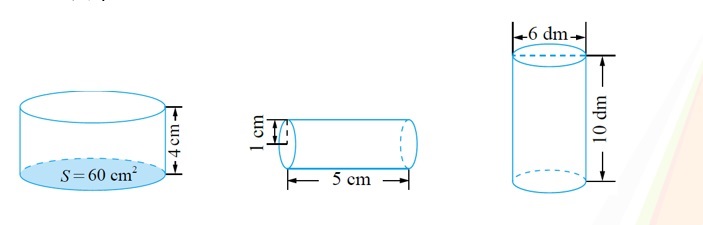
师：知道底面积和高就能求圆柱的体积，如果不告诉底面积，要求圆柱的体积需要知道哪些条件？

（设计意图：第一题通过生活中的实际问题，判断哪些问题是和圆柱表面积有关？哪些问题是和圆柱体积有关？通过辨析，沟通圆柱体积与生活实际的联系。第二题是与之前叠纸片的活动相呼应，给学生一个体积标准后再对纸片叠成的圆柱体积进行估计，在估算中继续发展学生体积量感。第三题是对公式的灵活运用，通过告诉半径和高、直径和高、周长和高，拓展对公式的理解和掌握，在公式的转化过程中培养学生量感。）

五、沟通联系，拓展延伸，发展量感

出示长方体，正方体、圆柱，形状不同，但它们的体积都可以用底面积乘高来计算，它们之间是否有一些我们不易察觉的联系呢？

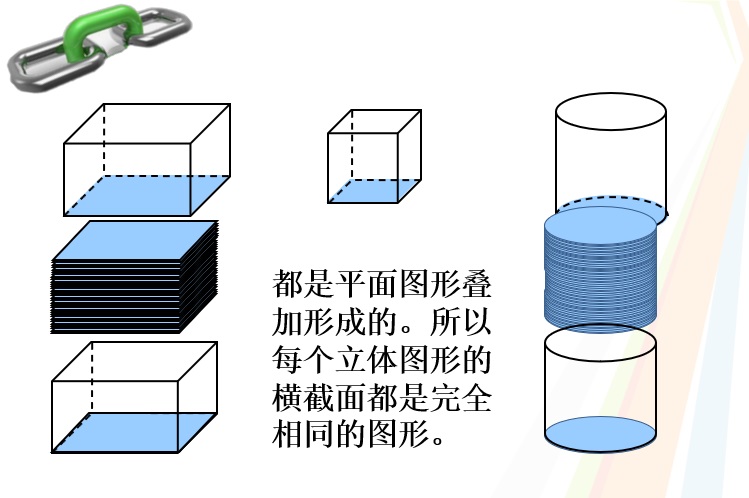
（通过沟通几种直柱体体积公式的内在联系，拓展对 “体积 = 底面积乘高” 这一公式的运用，拓展学生思维，在沟通交流中培养学生的量感。）

六．课堂小结

1．谈谈这节课你有哪些收获？

（设计意图：收获包括知识、能力、方法、情感等全方位的体会，在这里采用提问式小结，使学生畅谈收获、发现不足，既能训练学生的语言表达能力，又能培养学生的归纳概括能力；同时通过对本节所学知识的总结与回顾，还能使学生学到的知识系统化、完整化。）

七．板书设计

【第二次试讲反思】

在第一次试讲后，我们团队进行了深入研讨，把一些活动进行了调整和优化，练习的设计在巩固新知的同时也注重体积量感的发展和完善。整体效果较上一次有了明显的改观。学生参与活动的效率有了较大提高，学生的体积量感得到了较好的培养和发展。 这次试讲，我们邀请了学校全体数学老师参与听课与交流，以下是老师们的意见和建议。

优点：

1 叠纸片和硬币的活动设计较好，不仅让学生体会圆柱的体积与底面积和高有关，同时在叠加的过程中，感受体积的增加变化，发展体积量感。

2. 估 “水的体积” 的活动，调动了学生已有的体积量感经验，也同时暴露出学生体积量感的缺失，从学生的实际出发设计下面的体验活动，帮助学生把这些经验达成共识。

建议：

1. 前面部分流程设计：估计，量杯，堆正方体，比，给圆片硬币，比纸片和杯子底。借助杯子里水来估计纸片，打包（一定要打包），有助于学生量感的形成。

2、估 “水的体积” 活动时，第一个环节让学生根据生活经验估计，学生估计偏差较大，这时再为学生提供一个熟悉的圆柱形物体（如一瓶水，一瓶酸奶等），有了参考再让学生估，就能更接近实际结果，这样设计给学生提供了估的方法，也积累估的经验。

3. 今天这节课的量感体现：前面的活动压缩，就利用火腿肠，首先是同样粗了两根火腿肠，一根长，一段短，要让两根体积相同，把长的多余部分割了，然后是同样长的两根火腿肠，一根粗，一根细，要让两根体积相同，把长粗的多余部分割了，这个过程体现量感。

4. 学生利用展台汇报时，将立体的东西平面化了，不利于学生观察发现，可以借助慧道平台现场展示。

针对老师们的意见和建议，我们团队再次进行了研讨，吸收了部分建议，同时也坚守了我们之前的一些思考。

【教学设计】第二稿

【教材简析】 本课内容是在学生已经初步理解了体积和容积的意义、掌握了长方体和正方体体积计算方法的基础上学习的，长方体和正方体体积计算方法 “底面积 × 高” 对探索圆柱的体积计算方法有正迁移作用。本课的重点在于引导学生经历 “猜想与验证” 的探索过程，在探索中理解、掌握圆柱体积的计算方法，教材充分利用学生学过的知识作铺垫，采用迁移法，引导学生将圆柱体转化成已学过的立体图形，再通过观察、比较找两个图形之间的关系，可推导出圆柱的体积计算公式。

【教学目标】

1．通过具体情境观察、实物感知、实践操作等活动，感受物体体积的大小、发展学生体积量感。

2．通过圆柱与长方体的 “类比”，经历 “猜想与验证” 探索圆柱体积计算方法的过程，体会 “类比” 的数学思想方法。 3. 会计算圆柱形物体的体积和容积，运用公式解决简单的问题。

【教学重点】圆柱的体积计算。

【教学难点】圆柱的体积公式的推导过程。

【教具准备】圆柱的体积公式演示教具，多媒体课件

【教学过程】

一、首次感知，唤醒量感意识

1. 出示问题，揭示意义。

师：同学们，圆柱形的物体在生活中随处可见，下面的问题是和圆柱的什么有关呢？

生：体积。

师：这些问题都是求圆柱的体积，你能说说什么是圆柱的体积吗？

生：圆柱所占空间的大小就是圆柱的体积。

（设计意图：数学来源于现实生活，又应用于生活。《数学课程标准》强调数学与现实生活的联系，选择与学生生活密切联系的问题情境有利于激发学生兴趣，点燃探索新知的热情。）

2. 比较体积，产生量的需要

（1）估一估水的体积

出示 1 杯水

师：这个圆柱形杯子里装了一些水，水是什么形状的？谁来估一估这杯水的体积是多少？

师：这杯水的体积是多少呢？你有什么办法能得到水的体积？

生 1：倒入量杯量直接测量。

生 2：. 倒入长方体容器中，测量出长宽高计算体积。

师结合学生的汇报演示。

师：同学们估的结果和实际差距比较大啊！每个小组都有 60 个体积为 1 立方厘米的小正方体，小组内任意摆一摆，看看 60 立方厘米的小方块可以摆成多大的立体图形。

（2）出示生活中圆柱（接力棒）。

师：每一个物体都有体积，在估的时候可以先想一想 1 立方厘米 1 立方分米 1 立方米到底有多大，避免估计结果和实际相差比较大。

师：水的体积可以倒入量杯直接量。如果要求这根接力棒的体积，还能用刚才那样的方法吗？（不能）

师：那像这样的圆柱，它的体积应该怎样求呢？这节课我们就一起来研究 “圆柱的体积”（板书课题）

师：你可以先试着想一想，圆柱的体积可能和它的什么有关？ （学生可能会说：半径和高，直径和高，周长和高，面积和高）

（设计意图：学生对体积量感经验是有些缺失的，借助已有的经验，很难正确的进行估计。学生出现不同估算结果后，再通过实际量，与之前估的结果对比，可以对学生体积量感的经验进行修正，再通过摆 60 个小正方体的活动，进一步巩固学生体积量感。学生想到测量水的体积的方法非常好，但这些方法都具有局限性，求接力棒的体积就不能用到刚才的方法，这时让学生试着想想圆柱的体积与它的什么有关？这时学生会自动唤醒已有知识经验，将影响体积大小的因素指向到底面积和高上来，为后续的学习做好了铺垫。）

二、叠加实物，领悟（体积）量的要素

1. 感知体积与底面积和高有关 师：老师为大家准备了一些大小相同的圆片和一些硬币，请在小组内叠一叠。

要求：

（1）将纸片（硬币）一片一片往上叠。

（2）叠的过程：边叠边观察，你有什么发现？

（3）叠好后：组内观察或与周围小组对比观察，你又有什么发现？

（4）把你们的发现写在学习单对应的地方。

生 1：我发现一张纸片很薄，一张的厚度可以忽略不计，当很多张纸片叠在一起时就有了厚度，就得到了一个近似的圆柱。

生 2：在往上叠的过程中，高度在增加，体积也在增加，说明圆柱的体积与高有关。

生 3：第一小组叠的纸片（硬币）比我们小组高（底），圆柱的体积比我们大（小），说明圆柱的体积与高有关。

生 4：我们小组将 1 元的硬币和 1 角的硬币叠起来，发现高度相等，但 1 元硬币底面比较大，所以叠起来的物体体积大，说明圆柱的体积与底面积有关。

2. 回顾旧知，类比猜想

师：通过刚才的活动，我们发现圆柱的体积与它的底面积和高有关。猜一猜，到底有什么关系呢？能告诉我们为什么有这样的猜想吗？

生：因为长方体体积 = 底面积 × 高，所以我猜圆柱的体积 = 底面积 × 高。

（设计意图：动手操作是学生获得量感的重要途径，通过叠纸片的活动，不仅能感知形成的圆柱是圆形纸片面的叠加，还能感知圆柱的体积与高有关。通过叠硬币的活动，让学生感知圆柱的体积不仅和高有关还和底面积有关，学生亲身经历圆柱体积变化的过程，丰富了对圆柱体积量感的经验。同时在组内对比，组外对比中加深对体积与底面积和高的关系的体会。通过通过回顾长方体、正方体体积计算公式，通过类比猜想，唤醒体积量感的敏感以及对量的直接反应，学生很容易得出 “圆柱体积 = 底面积 × 高” 的猜想。）

三、操作验证，推导体积公式

1. 观看微课，启发思维

师：转化真奇妙，我们能把一个圆采用化曲为直、化圆为方的方法推导出了圆面积的计算公式。这个过程对你有什么启示？

生 1：不能直接求时可以尝试转化。

生 2：可以将圆柱转化成长方体。

（设计意图：借助微课，将圆面积公式推导过程的再现，为实现经验和方法的迁移做铺垫，也让学生感受到知识内在的统一。）

2. 动手操作，沟通联系

首学：

（1）操作：将圆柱转化成长方体。

（2）思考并交流：转化后的长方体与圆柱有什么关系？

（3）推导：圆柱体积的计算公式。 互学 小组交流自己的想法，做好记录，做好全班交流的准备。 群学 ：

（1）小组汇报，展开思维

生：（平均分成 8 份）转化后的长方体与圆柱的体积相等，长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高，长方体的体积 = 长方体的底面积乘高，所以圆柱体积 = 圆柱的底面积乘高。

教师追问：为什么长方体的体积与圆柱的体积相等。（等积变形）

（2）对比观察，拓展思维

师：将平均分成 16 份拼成的长方体与刚才的长方体对比，你又发现了什么？ 生：平均分成 16 份拼成的图形更像长方体。

（3）播放课件，加深理解

师：如果我们将圆柱底面等分成 32 份，64 份，甚至更多，然后再拼起来会是什么情况呢？ 生：分的份数越多，拼成的立体图形越接近长方体。

师：我们一起再来看看这个精彩过程吧！

师：老师想把刚才这个过程做成微课，让更多的同学能看到，你能给这个过程配一段解说吗？谁来试试。

生：圆柱通过切拼，转化成近似的长方体。长方体的体积等于圆柱的体积，长方体的底面积等于圆柱的底面积，长方体的高等于圆柱的高。因为长方体的体积等于底面积乘以高，所以，圆柱的体积 = 底面积 × 高。用字母表示：V=Sh。(板书)

3. 回顾梳理，建构模型

师：同学们，通过大家的共同努力验证了之前的猜想，我们再次回顾之前的活动，你发现了什么？（猜想、叠纸片硬币、切拼火腿肠、推理得出结论）

（设计意图：量感的培养需要丰富的活动经验。学生经历将圆柱转化成长方体的过程，更容易理解转化前后 “量” 之间的变与不变，感受量变背后的内在联系。在学生充分交流的基础上再通过观看课件，调动学生多种感官参与圆柱体积公式推导过程。在观察中理解，在比较中讨论归纳，让极限思维、转化思想有机的渗透在课堂教学中。这样的教学，不仅有利于学生理解算理，掌握算法，而且有利于发展学生的量感。）

四、运用公式，解决问题，固化量感

1. 下面的问题是求什么？

包装易拉罐（表面积） 水池蓄水（体积） 油桶涂漆（表面积） 多少石料（体积）

2. 估一估，算一算

（1）估一估：

20 张纸片的高大约 0.5 厘米，纸片的面积约 22 平方厘米，估一估，你们小组用纸片叠出的圆柱的体积是：（ ）立方厘米。

（2）算一算：

下面这堆纸片的高是 4.5 厘米，体积是（ ）立方厘米。算式是（ ）。

3. 知道底面积和高就能求圆柱的体积，如果不告诉底面积，要求圆柱的体积需要知道哪些条件？

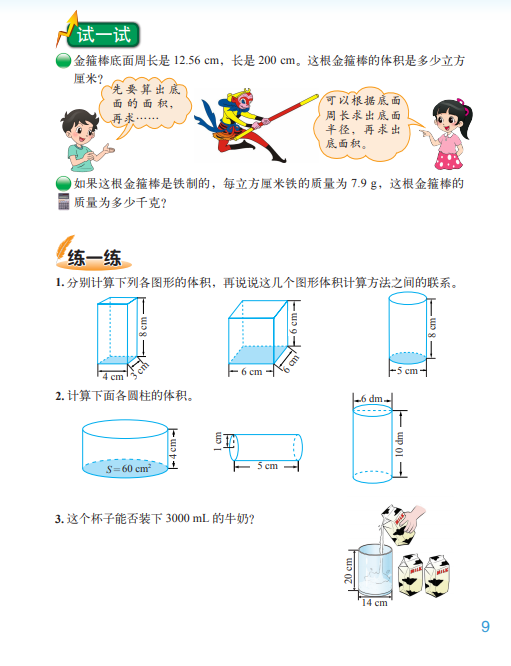
课本第 9 页练一练第 2 题：求下面圆柱体的体积。(单位：厘米)

（设计意图：第一题通过生活中的实际问题，判断哪些问题是和圆柱表面积有关？哪些问题是和圆柱体积有关，通过辨析，沟通圆柱体积与生活实际的联系。第二题是与之前叠纸片的活动相呼应，给学生一个体积标准后再对纸片叠成的圆柱体积进行估计，在估算中继续发展学生体积量感。第三题是对公式的灵活运用，通过告诉半径和高、直径和高、周长和高，拓展对公式的理解和掌握，在公式的转化过程中培养学生量感。）

五、沟通联系，拓展延伸，发展量感

出示长方体，正方体、圆柱，形状不同，但它们的体积都可以用底面积乘高来计算，它们之间是否有一些我们不易察觉的联系呢？

（设计意图：通过沟通几种直柱体体积公式的内在联系，拓展对 “体积 = 底面积乘高” 这一公式的运用，拓展学生思维，在沟通交流中培养学生的量感。）

六．课堂小结

1．谈谈这节课你有哪些收获？

（设计意图：收获包括知识、能力、方法、情感等全方位的体会，在这里采用提问式小结，使学生畅谈收获、发现不足，既能训练学生的语言表达能力，又能培养学生的归纳概括能力；同时通过对本节所学知识的总结与回顾，还能使学生学到的知识系统化、完整化。）

【第一次试讲反思】

学生量感的建立更多是依赖经验的积累。之前的学习，学生对体积量感已经积累了一定的经验，本课教学的重点是探索圆柱体积计算公式，但更重要的是在这个过程中激活学生原有体积量感的经验，进一步发展体积量感。为此，我们团队在深入学习相关理论知识的基础上，设计了多个活动，丰富学生对体积量感的体验。

优点：

1．知识的探究是主线，量感的培养是暗线，整个教学过程很好的处理了两者之间的关系，两条线齐头并进，不仅关注的学生对知识的掌握，也关注学生量感的培养和发展。

2．创设多个活动情景，让学生经历观察、操作、体验、感悟的过程，增强了整个探索活动的可视性，以推理、类比等教学方式帮助学生形成量感，使量感的培养变得更加真实和形象。例如，叠纸片的活动，不仅能感知形成的圆柱是圆形纸片的叠加，还能感知圆柱的体积与高有关，学生亲身经历圆柱体积变化的过程，丰富了对圆柱体积量感的经验。再如，在圆柱体积的推导过程中，让学生亲身经历将圆柱转化成长方体的过程，才能更容易理解转化前后 “量” 之间的对应关系，聚焦 “变与不变”，感受转化前后 “量 “的内在联系。

不足：

1．这节课对学生量感培养的点落实深度不够，如叠纸片和硬币的活动，不要局限于小组内的比较，可以拓展到小组与小组的比较，并呈现出直观对比的结果，不断丰富学生对体积大小的直观体验。

2．练习设计更偏向对知识的理解与运用，应思考如果通过练习帮助学生对体积量感进一步完善。

【教学设计】初稿

【教材简析】

本课内容是在学生已经初步理解了体积和容积的意义、掌握了长方体和正方体体积计算方法的基础上学习的，长方体和正方体体积计算方法 “底面积 × 高” 对探索圆柱的体积计算方法有正迁移作用。本课的重点在于引导学生经历 “猜想与验证” 的探索过程，在探索中理解、掌握圆柱体积的计算方法，教材充分利用学生学过的知识作铺垫，采用迁移法，引导学生将圆柱体转化成已学过的立体图形，再通过观察、比较找两个图形之间的关系，可推导出圆柱的体积计算公式。

【教学目标】

1．通过具体情境观察、实物感知、实践操作等活动，感受物体体积的大小、发展学生体积量感。 2．通过圆柱与长方体的 “类比”，经历 “猜想与验证” 探索圆柱体积计算方法的过程，体会 “类比” 的数学思想方法。

3. 会计算圆柱形物体的体积和容积，运用公式解决简单的问题。

【教学重点】圆柱的体积计算。

【教学难点】圆柱的体积公式的推导过程。

【教具准备】圆柱的体积公式演示教具，多媒体课件

【教学过程】

一、首次感知，唤醒量感意识

1. 出示问题，揭示意义。

问题：这么粗的柱子需要多少木材？一个杯子能装多少毫升水？这两个问题和圆柱的什么有关呢？ 说一说：你能说说什么是圆柱的体积吗？

2. 活动一：比较体积，产生量的需要。

（1）比较两个圆柱形水杯中水的体积（直接观察）。 想一想，水杯里的水是什么形状的？谁的体积大？

（2）比较两个圆柱形水杯中水的体积（无法直接观察）。 当我们不能直接观察得出结论时，你有什么办法？ 师结合学生的汇报演示。

（3）出示生活中圆柱（接力棒）。

如果要求这根接力棒的体积，还能用刚才那样的方法吗？ 还记得长方体和正方体体积怎么计算吗？谁来说一说。 大胆的猜一猜圆柱的体积可以怎么求呢？

（设计意图：创设比较体积的问题情境，学生借助已有的对体积量感的经验，能很容易比较出情景 1 中哪杯水的体积大，当不容易比较出体积大小时，学生会想到借助量杯测量或水的可变性转化成长方体测量并计算。但这些方法都具有局限性，求接力棒的体积就不能用到刚才的方法，这时通过回顾长方体、正方体体积计算公式，通过类比猜想，唤醒体积量感的敏感以及对量的直接反应，学生很容易得出 “圆柱体积 = 底面积 × 高” 的猜想。为后续的学习做好了铺垫。）

二、叠加实物，领悟（体积）量的要素。

1. 感知体积的变化与高有关。

（叠纸片） 叠纸片，看看你有什么发现？

小结：圆柱的体积与高有关。

2．感知体积的变化还与底面积有关。

（叠硬币） 叠硬币，你又有什么新的发现？

小结：圆柱的体积与底面积有关。 （设计意图：动手操作是学生获得量感的重要途径，通过叠纸片的活动，不仅能感知形成的圆柱是圆形纸片面的叠加，还能感知圆柱的体积与高有关。通过叠硬币的活动，让学生感知圆柱的体积不仅和高有关，还和底面积有关。学生亲身经历圆柱体积变化的过程，丰富了对圆柱体积量感的经验）

三、操作验证，推导体积公式 。

1. 观看微课，启发思维 观看圆面积公示推导的微课，你有什么启示？

小结：可以将圆柱转化成长方体。

（设计意图：借助微课，将圆面积公式推导过程再现，为实现经验和方法的迁移做铺垫，也让学生感受到知识内在的统一。）

2. 动手操作，沟通联系 。

首学：

（1）操作：将圆柱转化成长方体。

（2）思考并交流：转化后的长方体与圆柱有什么关系？

（3）推导：圆柱体积的计算公式。

互学：小组交流自己的想法，做好记录，做好全班交流的准备。

群学：

（1）小组汇报，展开思维

（2）课件演示，规范操作 课件展示将圆柱底面等分成 32 份、64 份……，在观察中明确分成的份数越多，拼成的立体图形就越接近于长方体。 3. 回顾梳理，建构模型 回顾之前的活动，你发现了什么？

（设计意图：量感的培养需要丰富的活动经验。学生经历将圆柱转化成长方体的过程，更容易理解转化前后 “量” 之间的变与不变，感受量变背后的内在联系。在学生充分交流的基础上再通过观看微课，调动学生多种感官参与圆柱体积公式推导过程。在观察中理解，在比较中讨论归纳，让极限思维、转化思想有机的渗透在课堂教学中。这样的教学，不仅有利于学生理解算理，掌握算法，而且有利于发展学生的量感。）

四、运用公式，解决问题，固化量感 。

1. 这根接力棒，底面积约为 13 平方厘米，高为 30 厘米，它的体积是多少立方厘米？

2 课本第 9 页练一练第 2 题：求下面圆柱体的体积。(单位：厘米)

（1）只列式不计算，要求列式之前先写公式。

（2）如果没有直接告诉底面积，要求圆柱的体积需要知道哪些条件？

3. 一个圆柱形无盖水桶，底面直径是 4 分米，高 5 分米，这个水桶能装多少水？

（设计意图：第一题是一道基础练习，解决之前提出的问题，巩固体积的基本计算公式。第二题是对公式的灵活运用，通过告诉半径和高、直径和高、周长和高，拓展对公式的理解和掌握，在公式的转化过程中培养学生量感。第三题安排了密切联系生活实际的问题，切实体验到数学来源于生活又服务生活，在解决实际问题中培养学生量感。）

五、沟通联系，拓展延伸，发展量感。

长方体，正方体、圆柱，形状不同，但它们的体积都可以用底面积乘高来计算，它们之间是否有一些我们不易察觉的联系呢？

（设计意图：通过沟通几种直柱体体积公式的内在联系，拓展对 “体积 = 底面积乘高” 这一公式的运用，拓展学生思维，在沟通交流中培养学生的量感。）

六．课堂小结

谈谈这节课你有哪些收获？

（设计意图：对本节所学知识的总结与回顾，能使学生学到的知识系统化、完整化，既能训练学生的语言表达能力，又能培养学生的归纳概括能力）