7年前 回复了 冯文婷 创建的主题› 展示大赛-2019 › 【2019 秋】山西汾阳府小冯文婷四上《路程、时间与速度》 |
学生学习复合单位的引入很棒,也让他们感受到复合单位表述的重要性
11年前 回复了 山东省刘勇 创建的主题› Q群交流 › 亿以内的数的大小比较方法还用讲吗(小学教学话题征稿) |
万以内孩子刚熟悉 4 位为一个单位元,那么将来接触到更大的亿,兆,需要有这个做基础的拓展,不能依我们老师们认定的” 就类化一下就行了”,这不太符合孩子的认知发展
12年前 回复了 山东省刘勇 创建的主题› Q群交流 › 难道仅仅是游戏 —— 关于数学好玩的思考 |
刘老师真的很用心,利用土豆切割来认识立体几何形体的结构很棒,很直观
12年前 回复了 山东省刘勇 创建的主题› Q群交流 › 发表文章的喜悦与思考 |
执著在一件有意义的事,在一件自己喜欢做的事上,持续的做就会愈做愈快乐,给刘老师 100 个赞
12年前 回复了 深圳宝安-孙明岩 创建的主题› 展示大赛-2019 › 【2013】网络团队深圳松岗二小孙明岩四上《卫星运行时间... |
孙老师,辛苦了,以下提出我个人的拙见,参考看看。ps 怕图片档出不来,所以我夹带了袝件档
l (出示图片卫星重 173 千克,绕地球一圈需时 114 分,)….. 卫星是 173 千克??这么轻呀!<呵,我自己的疑惑>
l 。。。结合这段内容,你能看出哪些数学信息?
师:你能得出一个我们学过的数学问题吗?
想法: 学生会不会提及 1970 年 4 月 24 日到 2013 年 6 月 11 日过了多久时间的时间问题,或是人造地球卫星一分钟绕地球几分钟的速度问题?如何导引他们进入你预设好的题目,建议也可以用另一种问法: 结合这段内容,大家猜猜看,老师想问你们什么问题?看谁能猜得到老师的心?
生:人造地球卫星绕地球 2 圈、5 圈、10 圈 …… 所需要的时间是多少?
<当学生提出问题点,则大大赞赏,你真厉害,竟然能猜中老师心中想要出的题目!想出其它问题的同学也要赞赏,再请他们继续猜想提出数学问题。>
l 师:该怎样计算呢?为什么要用乘法?
生:114×2=228 分 114×5=570(分) 114×10=1140(分)……
想法: 学生尚未回答,教师已经先提示 “用乘法 “?是否改成
师:该怎样计算呢?
生:用乘法!
师:那么若绕地球 2 圈、5 圈、10 圈,你们要怎么用乘法么列式呢?
生:114×2 114×5 114×10……
师:那么若绕地球 21 圈呢?甚至更多圈呢?你们能算出来吗?
。。。。。。。。。。。。。。。
l 在二、活动探究,获取新知中的第 3 点、估算结果:是否可以针对学生估算的结果进行与原数大小的猜测,例如:
生:我把 114 看作 110,把 21 看作 20,110×20=2200,所以 114×21 大约等于 2200。
师:那么,大家猜猜看,原数算起来,会比 2200 大还是小?为什么呢?
l 在<算法展示>中,。。。。同时请作者自己讲述思考过程,关注思路相同和思路不同的小朋友是不是都能理解这种算法,。。。。, 这个地方,有时也可以参杂另一种方式,请另一位同学来试著猜测作者的想法,猜完再请作者说说,那位同学说的对不对? 目的是让其它学生也能试著去读懂别人的想法,也可以让作者发表他的想法或做澄清。
l 5、算法展示:此部分,您的追问是很重要的!也可以让学生来进行追问。
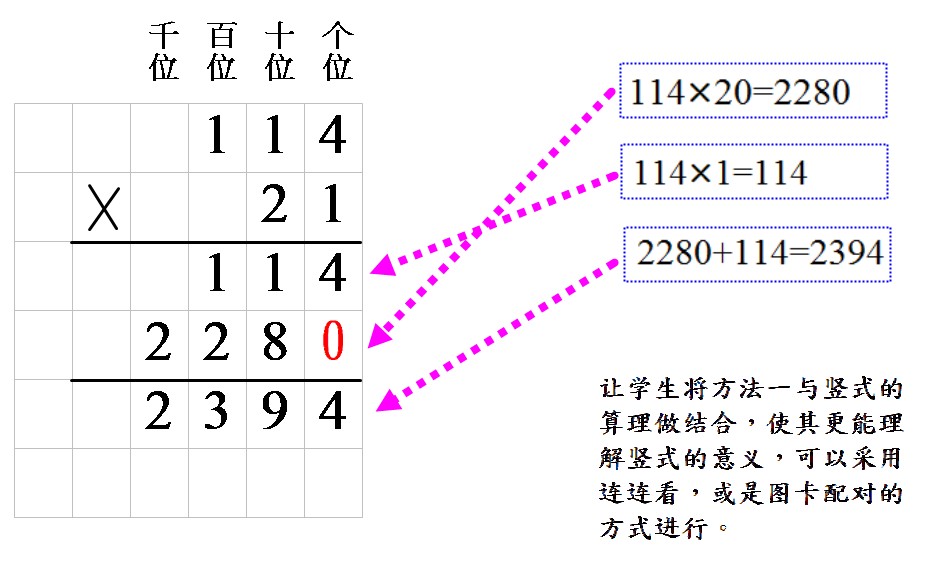
方法三:竪式算理的引入,如何才不会让它枯燥,其建议的方式如下,竖式的对齐,一开始也可以借助格子,上方加上位值名称,难点在于 114 乘以因数的十位数字 2 之摆放位置,是否借由格子及位置名,能帮助学生理解为何写在那个位置,因为是 228 个十。<如图>l 三、巩固应用,当堂反馈的 1、基础练习,是否改出 “那如果是绕地球 29 圈该用多少分钟呢?“这样才符合您后面的期望~“会不会有小朋友用 114×30,然后再减去 114×1 呢?“
l 2、提升练习。估一估,算一算。的三道题目,与主要课题的题目差异性挺大的,前面三位数 × 二位数,只实际练习到 2 题,即进入三种不同的题型,会不会负担过大,因为要类化到二位数乘三位数,竖式计算需要三层<除非你们准允学生将大的数放在上方>,三层的计算意义要理解,且要对齐,是有一些困难的,再加上中间有 0 的数字运算,或末尾有 0 的简便计算方法,若要学生彻底理解其意义,这可能得花更多的时间,全部要掌控在一个课时中,我不知收到效益会有多大?
图片:
12年前 回复了 绿萝花开 创建的主题› 展示大赛-2019 › 【2013】网络团队陕西汉中汉台区宗营镇中心小学韩杰二上... |
- 学生自己观察后举手说一说自己发现的数学信息.......... 让学生用一双小小数学眼去探索线索,很棒!
2。教师巡视指导,完成的,随机发放智慧星。(很好的策略,给了孩子马上的正增强,若怕他们等会不太会说,则可以给他们小小声的提示,如,你们刚才这个。。。地方说的实在是太好了,等会可以把这个好想法跟大家说说>
3。教师巡视指导,完成的,随机发放智慧星。(这个想法很棒,给予即时赞赏,可以有效增强孩子的信心,而赞赏的点尽量关注在关键点上的赞赏<如:哇,某某同学 “竟然 “想到用。。。。。>,而非一般性的赞赏<嗯,你很棒,你说的很好>。。
4。我有个小想法。。。也许在最后,可以选出几个好问题,配上情境图,贴在班上的数学角。。。让大家挑战解题,目的是,不是课堂中才能学习或挑战数学,随时都可以再挑战。。甚至鼓励继续再延伸出题,若可以的话,孩子一定有兴趣了,他们什么事都做得出来。。。出题的方式可以以情境图为中心,采 “心智绘图 “的形式往外扩充。。。应该会很不错的,估且不论学生做得好不好,但就是可以引发孩子的兴趣。。。呵,这是我个人粗浅的想法
12年前 回复了 山东省刘勇 创建的主题› Q群交流 › 关于学生不完成作业的思考 |
例一: 以一女生为例:拿出自动铅笔来,刚要写字,发现铅太短了,十分自然地压几下,好让铅长些可以写字。可当她写字时,才发现,铅并没有压下来!怎么办?再压几下吧!此次终于把铅压好了,刚写了几下(一个字还没有写完),只听啪得一声响,原来铅断了,怎么办?再压几下吧!其实,也就是说,这名学生从拿出铅笔到写字,足有五分钟,却一个字也没有写成!
通常孩子在刚开始习写字时,我们是不让他们用自动笔的,
因为自动的笔心细较易断裂,孩子握笔力道是无法拿捏的,一定会出现这种情况,这不是他们的错,
叵上自动笔的品质也有差异,让孩子屡次出现挫折,此时若再加上他本身就不太想习写字了,那就就可以一个很好的藉口
我们建议先拿铅笔来习惯,等习惯力道后,或长大些,再慢慢去使用自动笔
若我遇到这种状况,那么,我会拿一枝铅笔给他写,帮他解危,让他可以专心写好字
亦或是换笔芯,或 HB 或 2B,或再查寻一下呢一种笔芯较适合孩子
12年前 回复了 山东省刘勇 创建的主题› Q群交流 › 关于学生不完成作业的思考 |
" 计算 303×51 时,学生是这样计算的:303×50+303×1=15150+......
可以看出,学生会做的,他能将 303×51 分解成 303×50+303×1。。。已经非常好了
那么接下来就可能是他不太理解 “记录格式 “
若他能理解 303×51=303×50+303×1。。。所代表的意思是
303 有 50 个,以及 303 有 1 个。。。合起来即是 303 有 51 个。。。。
将 51 个 303 分成 50 个 303,和 1 个 303
然后分别算出答案是 15150 和 303,然后再相加起来
也就是学生在解决 303×50+303×1,要先写三步骤算式,然后学习将 它并成一个算式
即
303×50=15150
303×1=303
15150+303=15453
再合并一个算式。。。建议写在上述三步算式的右边,。。让学生清楚看到变化
303×50+303×1
=15150+303
=15453
再建议,以上述的写法让学生清楚对照
然后再引入一串横式 303×50+303×1=15150+303=15453
个人想法,请指教
12年前 回复了 山东省刘勇 创建的主题› Q群交流 › 关于学生不完成作业的思考 |
计算 303×51 时,学生是这样计算的:303×50+303×1=15150+......
12年前 回复了 林甸二小孙艳艳 创建的主题› 房间活动 › 2013 年 8 月 7 日呱呱北师大数学工作室活动安排 |
本帖最后由 台灣 - 何鳳珠 于 2013-8-8 22:03 编辑
844<如果没有一个老师能教全部的科目,那么为什么要学生学全部的课目呢?>
看来小叮当里大雄的这句话也挺有意思的,我们不妨可以思考一下.对学不来的孩子,多一点的包容。今晚很开心,我来自台湾盐水国小,能在这儿与各位交流。。。
845 我是一线老师,也经年累月一直在数学上钻研,但若,现在要我编辑一本全市或全国使用教科书,我自觉,我没有这个能力,所以,我用一颗谦卑学习的心,来阅读这本教材,我若是一个新手教师,或是第一次使用者,我会担心什么?我会用它吗?我会希望知道什么?怎样才可以让我一教就上手?更何况,我真的没教过北师大版,没有教过一年级,那我用怎样的心境来看这个教材呢?我可能无法回头看,所以只能以悦读教材的心情来解读。很简单,我只是想看看,小小孩他们是怎样来想数学?可以怎样带他们来玩数学,探究数学的神奇世界.
826 不知大家有没有发现,老师们教书教久了,都成了挑错高手,老挑学生的错,挑周遭人的错,挑家人的错,挑孩子的错,挑教材的错,..但,我想,教材再怎么编也不可能达到完美无缺,因为孩子有个别差异,老师也有个别差异,也许,换个角度,换颗好奇的心去看新教材,就像一年级新生拿到第一本新课本那种期待,那种心情一样,去发现....它里头有什么不一样?有什么新鲜有趣的挑战?臆测编写者的用意在哪?我们又可以怎么变化?有挑战,就会激发我们去思考,去尝试,那么教师的专业就在这不知不觉中积累了
827 倘若您发现里教材里编难了,那么,就用您的专业将它变简单,变合理吧!<鹍鹏小数工作室 - 关志成老师说的一句话,挺有感触的> 我想:这是我们老师跟别人不一样的地方,否则,就人人都可以当老师了,教师专业,从何而来,就从平时的自我学习,从教研学习,从网络学习,(在台湾只能单打独斗)各位应该很庆幸,此时此刻还能来到这儿学习,表示您还是很有学习力的,很幸福的,试想,有多少人想学但环境不许可无法学,又有多少人,早已放弃学习了呢?当您觉得教材很难,不可能实施,不可能教会学生,那么...就真的不可能了!当您觉得教材这样编有点难,那么表示还是有机会的!只是我们需要花点心思找到好方法!
828 第一次拿到教参,您会先读什么呢?通常,会直接看单元内容,如何教.是的,我也是,就像拿到一本书,我通常不会看序文,直接看内文,教参,也不例外,前那天,在看单元内容时,我心血来潮回头看了前面 17 页的使用说明,原以为会是枯燥的理论知识… 哪知,看得我心花怒放,惊讶连连,原来,理论与实务的结合,竟是这么的精彩,让我一下子又更进入状况了,更能了解这本教材他的编写意函,以及它可以无限拓展开发学生潜力的精彩点,也许,这对大家而言只是理论的推广,但,就我走在多年的创意数学上,两者之间是有高密度的契合,我终于明了武秀华老师她为什么跟我说,跟着这个编写组八年,她收获非常大,因为他们一直在努力,做读懂学生、读懂教材、读懂课堂的研究。
829
在这内容中,编辑组听进老师们的声音了 , 改了内容,所以有了第四版的诞生 .. 因为没有一份教材是完美的 , 也没有人能拍胸脯做保证 , 即是专家也是如此,编者尽心且虚心接受批评建议 ,
让这份教科书更完美 , 读者也用开放的心去欣赏它… 使用它 ,.. 挖掘它的好 .. 且记录它未完善并可以再改进的建议参考,容许我读其中的几句,给老师们听听…
我们老师特别需要给孩子空间,特别需要走近孩子,欣赏孩子们的创造,分享孩子的智慧。
在孩子们提到各式各样的问题时,你可能会一时不知所措,请你不要担心,我们做任何事情都是由无序走向有序的,这一个过程就是教育。
在你遇上各式各样的问题时,不要抱怨,改革需要我们放下曾经不恰当的经验,不断适应新的时代,如果你让孩子获得了数学学习的好奇心和自信,愿意去独立思考与合合交流,学会了思考,你就是成功的教师!
在你遇上困惑时,想一想什么是更适合学生成长与发展的,想一想我们自己和同伴是怎样解决问题的。如果还有问题,请联系我们。
830 831 我非常喜欢 "编者小语"p16-17.... 是我多年来对数学教育所追寻的目标… 虽然我不是本科生 (我们这儿称数学系), 但在我研修了数学教育系后才知道,原来。要这样教数学,才是真数学…. 也就是让数学课室真正活化起来,那样才不会有太多学生提早放弃数学… 变成教室里的客人
832
在这儿 , 我提出我看到这份教材的特色:
师生共同围绕一个问题展开探讨,这让我想象到课室的情景,会是一个很热络的讨论文化,… 这是台湾正在推行的学习共同体概念… 也许课室会乱,但,这是开始,会经历的,一旦形成共识后,那么数学课就是一堂有趣的课了… 很多老师实施过… 就我接触过的山东刘伟元老师,吉林长春的张辛欣老师.. 还有许多老师都有这样的经验,这在于我们老师愿不愿意跨出这最艰难的第一步,让自己不再讲台上唱独角戏了…[也许,还是挺困难的,但曾经试过总比都没试过的好,这是我的想法
833 从课本的编排可以清楚看到,新课程将说数学、做数学,彻底的融入在教学过程中,孩子们学会用数学思考的方式来解决生活问题,孩子的心中有数学,面对生活中的问题,会用数学的方式观察、思考、讨论与解决问题,数学学习的正向质变,从知识、技能与情意中高度展现数学力,这样的数学学习,谁不爱?
834 835
也许,我们都可以想想,就我个人的体悟 , 可以这样去思考....
当教材不变时,老师的教法可以一成不变,永远不变的教<不好>
当教材不变时,老师的教法可以改变,可以依据学生的个别差异或时代变迁而改<好>
当教材变时,老师的教法还是可以坚持不变<不太好>
当教材变时,老师的教法也时时创新<非常好>
让学生当教室的主人,老师们总是会担心的,但没跨出这一步,怎知会不好呢?... 很多都是因为我们心中存在 “难 “,所以迟迟着不行动,也许日复一日,永远用的是同一种模式吧!
836 接下来我想跟各位老师分享,我所看到较有感悟的一些片段…… 也许 , 我的看法不得到位 .. 那么也请多包涵
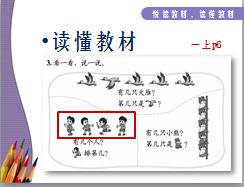
看图<一上 p6>大雁与接力问题
原先的质疑是,书上怎没说清楚是由哪边数起?是因为文字都是由左而右,所以自然所有数物都是由左而右数起吗?再来,一年级新生上第一堂数学课,他们未有接力的实际经验,能理解图中接力的顺序吗?后来,回头看了教参,才知道,原来答案是可以不同的,只要学生能说得出来表示已经理解” 序数” 所代表的意义了
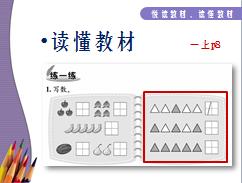
837 一上 p8 原先我想:就是教孩子,看一个涂色的三角形,就写1,看到3个,就写3,就这么简单,但看了教参后,才知道,原来,不是老师说,而是让学生说说,1是什么?<灰的?白的?>老师都说太快了,也就是说,“我们都太会,太行了!“不知能否理解我的意思?看了教参后,才知道,原来,也可以改变,问问孩子,若格子里写的是4,那代表什么?也就是尽可能提供一些变式,让孩子们的思考更灵活。
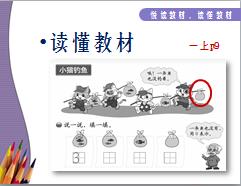
838 一上 p9 这是认识 0 的单元,不知有没有记错,这个地方与原先的第三版教材好像有所不一样,曾经听泉州师院的苏明强教授说过,原先小猫的钓竿上是没有袋子的,新版增加了一个空袋子,目的是融入了集合的思想,我觉得这样的改变是非常有意思的。
840
839 一上 p11 看到这个图,或许有老师认为很简单,就是六个铅笔盒,可以用六个棒子表示,六个三角形表示,也可以用手指表示,也可以写成 8。倘若只是如此简单带过,那么可能还不够到位,因为这是个由<实体物→半具体抽象→抽象数字符号>重要过程,它需要用好的方法引导,绝不能轻轻带过,否则学生会不知其所以然,同时,在中间三角形的示意图中,出现了白色的底框图,这好像也与三版教材不同的地方,是希望能渗透集合思想。
840 其实,说简单了,就是在教学课堂中,老师多一份:你是怎么想的?.. 的问询,学生多一些:我的理解是… 的表达,独立思考的精神就在这潜移默化中滋生了。老师们的教研学习,不也是这样的吗?经由经验的互相交流激荡,你是怎么想的?我的理解是…. 我们的教师专业不也就在此慢慢增生了吗?
841 教师永远是一部活的教科书 .. 华应龙老师的这句话说得真好,「” 教” 与” 学” 密不可分,唯有对学习者『学习』的深入了解,教师才能找到教学的施力点。」… 教材再怎么变 , 其实关键点 , 都在我们老师。很高兴与大家共同学习,愿在教育的路上共同成长,许孩子一个美好的未来,别让他们太早放弃数学。
图片:














13年前 回复了 李明伟 创建的主题› Q群交流 › 教学案例的分享暨问题答疑主题活动 — 特级教师王永 |
王老師您好..
- 定理和定義怎麼區分?當記不住哪條是定理?哪條是定義?有方法可以區分嗎?
這牽扯到我們在教小學生平面圖形的概念,
當我們提問:怎樣的圖形是平行四邊形?是要學生說定理還是定義?
倘若學生回答~一組對邊相互平行且等長的圖形就是平行四邊形,這是定理還是定義呢?
若再依據他的回答追問:那另一組對邊會相互平行嗎?為什麼?
<這個部分小學生懵懵懂懂,我也不知怎麼跟他們說明白,因為可能牽扯到一些證明>;
通常我們都是希望歸結到~兩雙對邊相互平行,是吧!
需宣告這是"定義"嗎?
不能用"一組對邊相互平行且等長的圖形就是平行四邊形"來做結論呢?學生迷惑了!有時我也迷惑了,
我可以說"兩條對角線互相垂直平分的四邊形就是菱形",這是不是定理?學生這樣說行嗎?
那由這句話"兩條對角線互相垂直平分的四邊形就是菱形",又如何與平行四邊形搭在一起呢?
如何說明兩條對角線互相垂直平分的四邊形其對邊會相互平行呢?
13年前 回复了 李明伟 创建的主题› Q群交流 › 教学案例的分享暨问题答疑主题活动 — 特级教师王永 |
- 定理和定義怎麼區分?當記不住哪條是定理?哪條是定義?有方法可以區分嗎?
這牽扯到我們在教小學生平面圖形的概念,
當我們提問:怎樣的圖形是平行四邊形?是要學生說定理還是定義?
倘若學生回答~一組對邊相互平行且等長的圖形就是平行四邊形,這是定理還是定義呢?
若再依據他的回答追問:那另一組對邊會相互平行嗎?為什麼?
<這個部分小學生懵懵懂懂,我也不知怎麼跟他們說明白,因為可能牽扯到一些證明>;
通常我們都是希望歸結到~兩雙對邊相互平行,是吧!
需宣告這是"定義"嗎?
不能用"一組對邊相互平行且等長的圖形就是平行四邊形"來做結論呢?學生迷惑了!有時我也迷惑了,
我可以說"兩條對角線互相垂直平分的四邊形就是菱形",這是不是定理?學生這樣說行嗎?
那由這句話"兩條對角線互相垂直平分的四邊形就是菱形",又如何與平行四邊形搭在一起呢?
如何說明兩條對角線互相垂直平分的四邊形其對邊會相互平行呢?
13年前 回复了 李明伟 创建的主题› Q群交流 › 教学案例的分享暨问题答疑主题活动 — 特级教师王永 |
新課標的課程編緝,頗重數學基本思想的導入,如何讓一線老師能在短時間內具體明瞭這些課程的轉變,並在課室中落實呢?