团队研磨图片

《圆的面积（一）》教案 2 稿反思

陕西省汉中市教研室基地 付枝波

《圆的面积（一）》教案 2 稿对教材和学情分析恰当，教学目标、重难点定位准确，表述清楚，教材挖掘充分，教案设计趋于合理。通过试课和再讨论，我们发现教案 2 稿有以下几点需要调整和改进的地方：

1. 个别环节难度太大，需降低难度。

新知探究第一环节数方格中，圆的半径 5 厘米偏大，导致学生难以很快数出正方形个数，可以改为半径 2 厘米。

2. 教学容量偏大，应进行适当的舍弃。

开课时对平面图形面积计算的复习可以略处理，省去演示环节。

引导学生发现圆的面积与圆外正方形面积之间的倍数关系，并用字母表示，再通过教师演示推导过程，回归到面积计算公式。冲淡主题，且偏难，应舍去。

3. 教学的核心环节不够突出，应再加强。

公式推导环节学生基本不会去转化成长方形，且后续的推导与平行四边形如出一辙，没有必要同时存在。相比之下，学生仅仅通过一次转化就形成公式就有些单薄。所以这里需要加强。可以设计 8 等份圆和 16 等份圆两种拼的活动，外加课件演示 32 等份圆、64 等份圆的拼接，丰富学生感性认知，渗透极限思想。

4. 个别环节的深度不够，可以再挖掘。

最后一道练习题可以对多边形面积计算进行提示性讲解，可以将数学文化渗透、爱国主义教育融进去。

1 稿反思:《圆的面积（一）》教案 1 稿对教材和学情分析恰当，教学目标定位准确，但重难点表述不够清楚。教材挖掘充分，处理较为大胆。其中将数方格求圆的面积与面积公式推导相融合环节略显牵强，但对于丰富课程内涵、及发展学生量感又有很大价值，仍存在争议，暂时保留，待进一步论证后决定取舍。圆的面积公式推导环节，按照探究提升应该是由圆到平行四边形和由圆到长方形两次实践操作推导，设计中缺少了对拼长方形的相关汇报，所以应当增加，教学时要注意主次关系。练习环节习题缺乏支撑，需要增加具体题型设计。板书可以增加图示（箭头），以呈现对应关系。

《圆的面积（一）》教案 1 稿

陕西省汉中市教研室基地 付枝波

【教学内容 】

北师大版小学数学六年级上册第一单元第 5 课时，教材 13—14 页。

【教材分析】

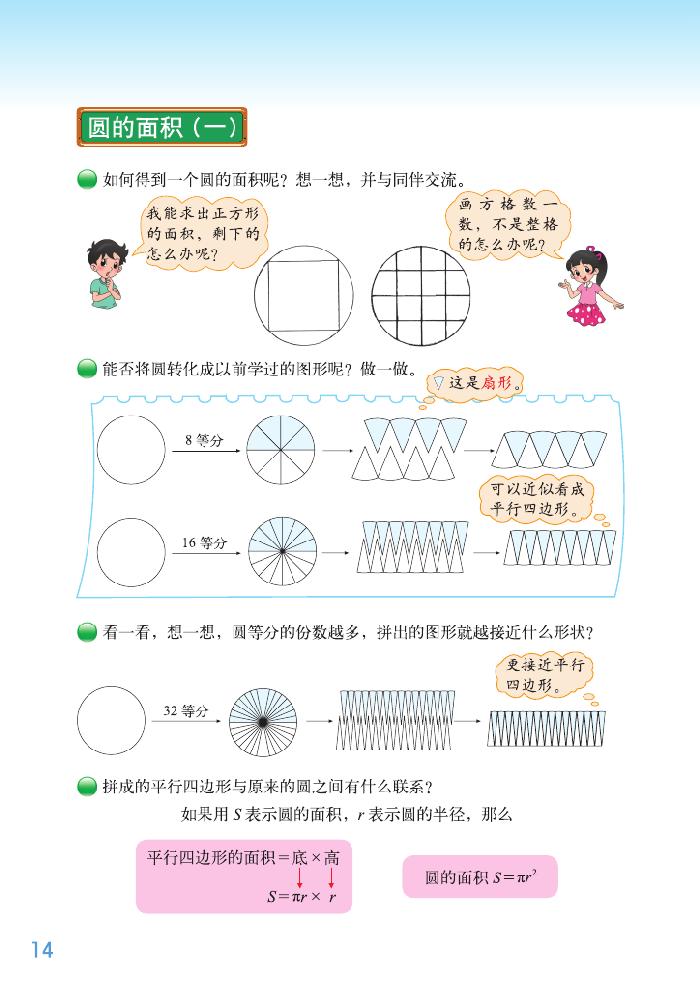
圆的面积是在学生学习了很多平面直边平面图形周长、面积，认识了圆的特征、学会计算圆的周长基础上进行教学的。这是第一次出现曲边平面图形的面积计算，教学的关键在于让学生充分经历圆的面积计算公式的探究过程，推导出圆的面积计算公式，并能灵活应用公式解决实际问题。因此本课的教学应紧紧围绕 “转化” 思想，引导学生联系已学知识把新知识纳入已有知识中分析、研究、归纳，从而完成对新知的建构过程，建立数学模型，发展空间观念和量感，培养分析、解决问题的能力。

【学情分析】

通过之前的学习，学生学会了很多关于平面直边图形周长、面积、体积的计算，已经具有一定的抽象和逻辑思维能力，具备了初步的猜想、验证、推理、概括等数学活动经验，对转化的数学思想有了多次感悟。本节内容从认识直边图形发展到认识曲线图形，又是一次飞跃。如何将圆转化为之前学过的图形，尤其是面积计算公式的推导过程，这些对于学生都颇有难度，需要教师适时的引导和启发。他们喜欢探究性、挑战性的学习活动，渴望得到数学史、数学文化的熏陶。

【教学目标】

1. 经历数方格、剪拼、推理等数学活动，探索并掌握圆的面积计算公式，并能初步运用公式正确计算圆的面积，构建数学模型。

2. 进一步体会 “转化” 的数学思想方法，感悟极限思想，增强空间观念，发展量感。

3. 体会数学与生活的联系，感受用数学的方式解决实际问题的过程，提高学习数学的兴趣。

【教学重难点】

重点：进一步理解面积的含义，圆的面积计算公式的推导和应用。

难点：圆的面积计算公式的推导，数学思想的渗透。

【教学准备】

教具：圆的面积演示教具、多媒体课件。

学具：16 等份的圆、剪刀、学习单。

【教学过程】

一、复习导入

   1. 说一说我们如何得到平行四边形的面积的？三角形、梯形呢？（数方格、转化）课件出示相应图形及转化过程。

2. 创设情境，揭示课题：一头牛被拴在木桩上，它能吃到草的面积是多少呢？从图中，你知道了哪些信息？（绳子长 5 米）牛能吃到草的面积是哪些地方？（课件演示）怎样得到这个图形的面积呢？揭示课题。

（ 设计意图： 通过对直边平面图形面积计算以及面积计算公式推导过程的回顾，重温 “数方格” 和 “转化” 的数学思想方法和活动经验，为新知教学做铺垫。以学生熟悉的生活化情境导入新知，一方面激起学生学习的兴趣，另一方面为后面圆面积的学习提供载体，同时让学生感受到数学来源于生活。）

一、合作交流，探索新知

（一）初步商讨，制定研究方案，分别实验

1. 方案一：用数方格的方法，先将圆分割成若干个单位面积（平方分米），再数出它所包含的单位面积个数。

根据学生提议，教师适时呈现被分割成单位面积的圆，并发放学习单到学习小组，指导研究，汇报形成结论。

质疑：你觉得圆的面积和什么有关系？（与半径有关系、与直径有关系、与正方形的面积有关系）

（ 设计意图： 借助已有学习经验，利用数方格的方法较为准确地得出于圆的面积。在这一过程中体会求圆面积的实际含义就是求圆所包含单位面积的个数。通过教师质疑引发学生深层次的猜想，发展学生量感。）

2. 方案二：用转化的方法，对圆进行分割，然后拼成已经学过的图形，研究面积。

根据学生提议，适时呈现分割方法，发放 16 等分圆的学具及学习单，指导学生将圆转化为近似的平行四边形，计算面积。

我拼成的是（ ）形

（   ）形的（   ） 分米 （   ）形的（   ） 分米 （    ）形的面积 平方分米

（ 设计意图： 这是一个开放性的探究活动，学生将通过学具的操作将圆转化为平行四边形或长方形，并初步发现转化前后图形各部分的关系，进而利用公式求出面积。）

（二）回顾实验过程，推导形成圆的面积计算公式。

1. 试填空，说一说拼成的图形的各部分与圆有什么关系。

将圆分割成若干等分，可以拼成一个近似的（ ）形，拼成的（ ）形的（ ）相当于圆的（ ），（ ）相当于圆的（ ）。

因为：（ ）形的面积 =  （  ）   × (  )，

所以： 圆的面积 =(        ) × (     )。

2. 教师引导形成字母公式。

3. 回顾数方格中所提出的：圆的面积和正方形的面积有关，进一步推导形成公式。课件呈现推导过程：

s=d×d×0.785

=(2×r)×(2×r)×0.785

=4×0.785×r×r

=3.14×r×r

 ≈πr²

（设计意图：在上一个活动的基础上对转化前后对图形各部分的关系进行更深入的研究，抽象出圆的面积计算公式，并用字母表示。通过教师介绍，将数方格时发现的圆的面积与圆外正方形的面积之间的关系进行再推导论证，与圆的面积计算公式实现辩证统一，加深学生对圆面积计算公式的记忆，开拓学生视野。）

三、巩固应用，拓展练习

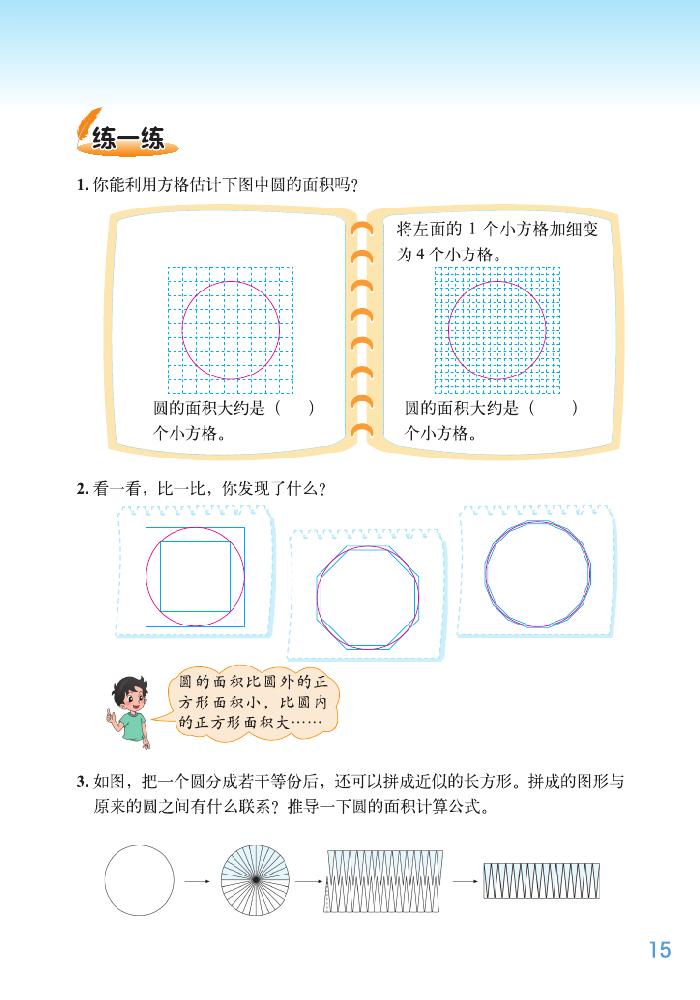
1. 利用方格图估计圆的面积。

2. 我画你猜再计算。同桌两人一组，一人以整厘米为半径画圆，另一人估计面积，再共同运用公式计算面积，进行验证。

3. 看一看，比一比，你发现了什么？

引导发现：圆的面积比圆外多变形的面积小，比圆内多变形的面积大。

将多边形分割成三角形，启发思考：也可以用这种方法研究圆的面积。

（ 设计意图： 通过三道题目分层次对教学内容进行巩固和拓展。其中第一题旨在巩固数方格求圆面积的方法，发展学生量感；第二题旨在让学生在估测和运用公式计算中发展量感，记忆公式；第三题旨在与柳慧的割圆术相联系，向学生渗透数学文化，介绍探索圆面积计算的其他途径。）

四、全课总结，回顾反思

本节课你有了哪些新的收获？我们是怎样得到圆的面积计算公式的？今天的学习对你今后的数学学习有什么启发？

（ 设计意图： 通过对学习过程的回顾和学习成果的总结，帮助学生进一步厘清知识脉络，构建知识框架，总结、积累数学活动经验。）

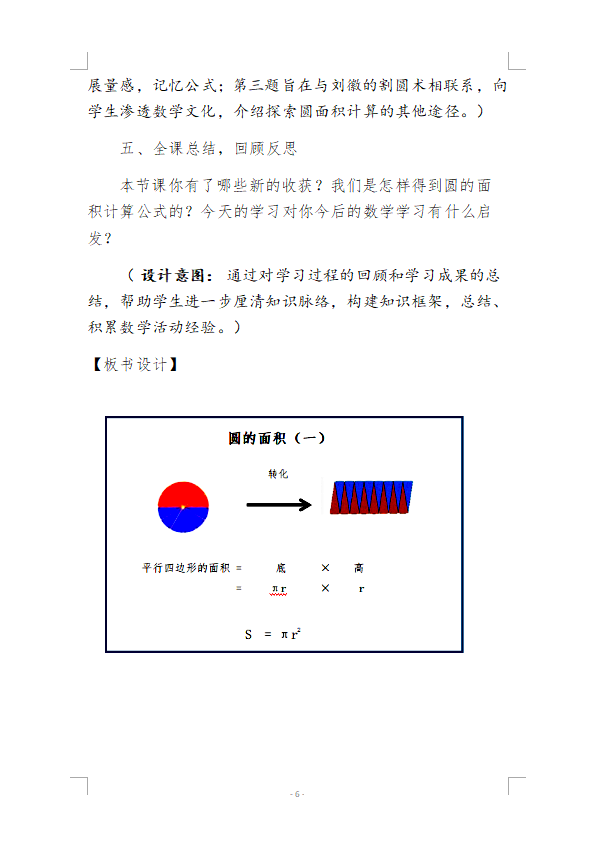
【板书设计】

圆的面积 (一)

转化

新的图形 已学过的图形

平行四边形形的面积 ＝ 底  ×  高

圆的面积 ＝圆周长的一半 × 半径

S     ＝  πr      ×  r

S ＝  πr²

选课思考：学生对单位量的感知相对容易，但对叠加量的感悟就尤为困难。这是一次很好的交流学习机会，所以我们团队想从叠加量的感悟方面着手研究，希望实现更强的思维碰撞。《圆的面积（一）》主要发展学生对叠加量的感悟能力，即圆中包含单位面积个数的估测和计算。它也是数学教材中十分特殊的一课，是平面图形面积的收尾课，又是曲边立体图形表面积、体积探究的基础课。同时这节课也有对空间观念、数感、数学推理、数学建模等多方面的教学目标要求，我们想尝试一下探索如何将多种数学素养的发展在一节课中有机融合。