彭建华

教学设计（终稿）

一、独立研习 探寻新知

师：今天我们这节课讲从一个故事开始，故事的名称叫《换与不换》。（播放故事视频）

故事内容：在很久以前，有一个财主，他特别喜欢炫耀自己的财富，有一天他突发奇想，把自己的金元宝制作成一平方分米大的金片，然后贴在客厅的一面墙上，只要有客人来，就能看到这些金片，不就能显示出自己的富有了吗。这个消息很块就传了出去，很多人都前来观看，有一天，来了一个商人，商人说：“我也想有一些 1 平方分米的金片，可我的手里只有 1 平方厘米的金片，我用 10 片和你换一片，你换吗？” 财主说：“不换，10 片 1 平方厘米的金片明显没有 1 平方分米大”“那 50 片呢”“50，算了，还是不换了吧！”“哎，那就 80 片换你一片吧！”“80 片，我考虑一下吧！恩……..” 财主拿不定注意，不知道自己该换还是不该换呢？

师：孩子们，如果你是财主，你是换还是不换呢？（多问几个孩子换还是不换）

预设：有的孩子说换，有的孩子说不换。

师：说一说你们换与不换的理由是什么？

预设：有的说 80 片那么多，可以换，换了就赚了。有的说不换，1 平方分米米能换 100 个 1 平方厘米，换了就亏了。 师：有什么办法能证明该不该换？

生：我可以用 1 平方厘米的来摆

生：我可以画

生：我可以算（说道算的情况比较少）

师：那就用你们的方法去验证一下吧！

生：操作验证（给予学生充分的探究时间）

设计意图：通过故事激发学生的学习兴趣，同时从 10 片、50 片到 80 片让学生体验量的变化，引起学生质疑，要多少片才能换。在这个过程中，学生以及初步的进行了换算，通过换算才能比较，换就得找个标准换，体会换算的必要性。而这个过程又是学生的一个初步猜想过程，为后面的想象类比推理打下基础。

二、同伴研讨 探究疑惑

师：孩子们找到这么多的方法，现在就请孩子们在小组内用你们的方法验证一下吧！

生：组内研讨后汇报

（一）摆

生 1：一行摆 10 个，摆 10 行，刚好就是一个 1 平方分米的正方形。

生 2：10×10=100，也就是说这个正方形的面积是 100 平方厘米。所以 1 平方分米 = 100 平方厘米。

（二）画

生 1：因为 1 分米 = 10 厘米，边长为 1 分米的正方形面积为 1 平方分米，10×10=100 平方厘米，所以 1 平方分米 = 100 平方厘米。

（三）算

生：1 分米 = 10 厘米，10×10=100，所以 1 平方分米 = 100 平方厘米。

师：从刚才的操作中，我们都能证明 1 行有 10 个，知道为什么一行只能贴 10 片吗？

生：因为 1 分米 = 10 厘米

师：你认为财主和商人换了吗？（多请几个人来回答）

生：换了

师：我们一起来看一看？（播放视频）

视频内容：财主和商人换了，又叫来了工匠，一行帖 10 片，2 行，3 行，4 行 5 行 6 行 7 行 8 行，遭了，我亏大了。 师：说一说，财主发现了什么？

生：他亏大了，少了 20 片。

师：也就是说，1 平方分米的金片能换多少个 1 平方厘米的金片。（板书）

生：100 个

师：接下来，我们一起来玩个游戏，游戏的名称是我说你拿。5 平方分米

生：一个拿 5 张 1 平方分米的，一个拿 5 袋 1 平方厘米的（每袋 100 个 1 平方厘米的）

师：300 平方厘米

生：一个拿 3 张 1 平方分米的，一个拿 3 袋。

师：商人又来了，他想用 1000 个 1 平方厘米的金片换 1 片 1 平方米的金片，你换还是不换呢？（多请几个人来说）

生：有的换，有的不换

师：能不能换，请大家在小组内讨论一下吧！

设计意图：学生通过多种操作，证明换还是不换。在活动中积累经验，为后续的想象类比推理打下基础；同时通过活动找到换算的标准，再通过游戏巩固换算的经验。不同的方法对比，都能发现一行有 10 个，因为 1 分米 = 10 厘米。同时又接上故事，让学生用 1000 个 1 平方厘米换 1 平方米，给学生提供更广阔的想象、类比、推理的空间，从数据变化中有一个量的感受。

三、团队研述 探索提炼

师：学生汇报

生：我不同意换，因为 1 平方米 = 10000 平方厘米的，8000 平方厘米不到 10000，所以不能换。

师：你怎么知道 1 平方米 = 10000 平方厘米的？

生：因为 1 平方分米 = 100 平方厘米，我想 1 平方米 = 100 平方分米，100×100=10000 平方厘米。

师：你有怎么知道 1 平方米 = 100 平方分米的？

生 1：因为用 1 平方分米的去铺，一行可以铺 10 个，可以铺 10 行，10×10=100

生 2：因为 1 米 = 10 分米，10×10=100 平方分米

生 3：因为可以把 1 平方分米的正方形想象成 1 平方米的，也能画 100 个

师：让学生到黑板上演示板书（边说边写）

师：那我们也来验证一下吧！（出示 1 平方米的图）谁能用图来说一说呢？

生：一行有 10 个 1 平方分米，有 10 行，一共有 100 个 1 平方分米，1 平方分米又有 100 个 1 平方厘米，就有 100 个 100，所以 1 平方米 = 10000 平方厘米的。

师：我们再回到刚才的问题，用 8000 个 1 平方厘米能换 1 平方米吗？

生：不能

师：从刚才的问题中，我们知道了平方米和平方分米的换算标准是多少呢？

生：100

师：平方米和平方厘米呢？

生：10000

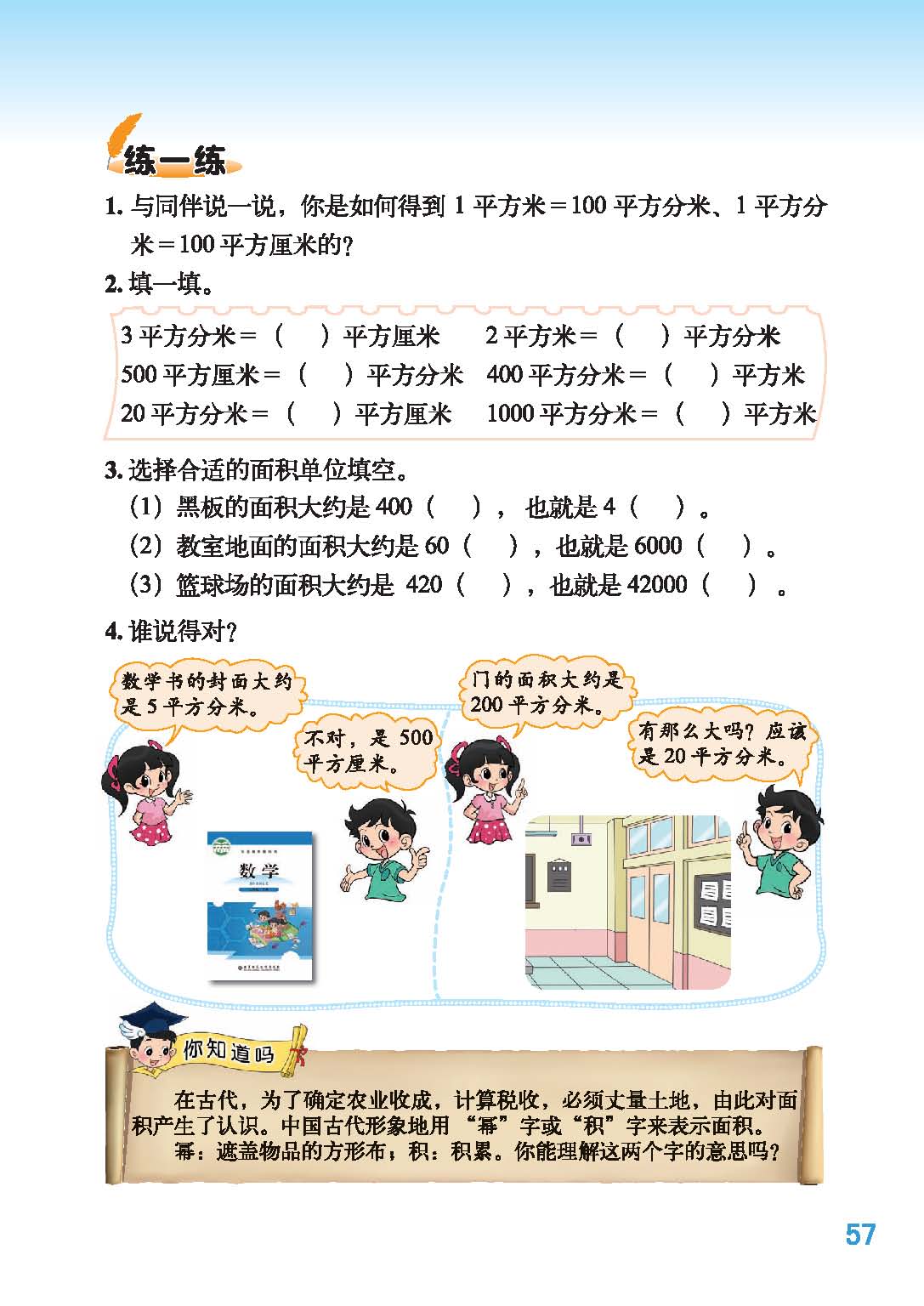
师：一天，笑笑和淘气争吵了起来，你能帮他们判断出谁对谁错吗？PPT 出示教材 57 页第 4 题。

生 1：淘气和笑笑都对，因为 5 平方分米 = 500 平方厘米

生 2：门大约有 2 平方米，也就是 200 平方分米，所以淘气错了。

师：讲述你知道吗？你能理解 “幕” 和 “积” 吗？

生：..........

师：请孩子们在课后利用今天学习的知识设计一下自己的班级展示栏吧！下课

设计意图：通过学生小组合作，再全班交流汇报，让 “理” 更明，让 “感” 更深。

教学设计（终稿）构思

1、用故事情境贯穿课堂始终，即提高学生的学习积极性，又让学生在故事中体会换与不换，为什么 “换”，同时数据的积累变化，体验 “量” 的累积，并发展量感。

2、用游戏的形式让学生体验 “算”，怎么用标准换算量进行换算。

3、提高学生想象，类比推理的空间，发展学生的空间想象能力，从而发展量感。

第二稿教学反思

第二稿的教学中，注重学生从生活中体验，根据需求进行换算。因此设计了瓷砖的长和宽分别为 3 分米和 20 厘米。虽然学生在课堂中能够体会把两个单位进行统一，分别得到 6 平方分米和 600 平方厘米，但是学生不明白为什么要把这两个数据分别用不同的单位来描述，容易造成误解，同时因为电脑显示屏无法准确的显示出实际物体的大小，而是按等比例缩小的，但学生所看到的和实际的是不一样的，也容易给学生造成误解。不利于学生的量感培养，因此在第三稿的教学设计中，会对本环节做出修改。

在第二稿的教学设计中发现，面积单位的换算比较枯燥乏味，学生在课程过半时就没有了积极性，因此在第三稿的教学设计中加入适当的情境，提高学生的积极性，同时也更利于学生对量感的发展。

在第二稿的教学设计中，学生的空间想象、类比推理相对不足，因此在第三稿的教学设计中要加大这方面的设计。

第二稿教学构思

1、重新定位教材，把教学定位到换算上。即为什么要换算 —— 怎么换算 —— 怎么用换算

（1）为什么要换算

我想要让学生从生活实际中体验，换算是一种需要，因为需要，所以才换算；也是一种计算的需要，要统一单位。

（2）怎么换算

从为什么要换算中，要学生体会到要先找标准 1 平方分米 = 100 平方厘米，1 平方米 = 100 平方分米，用标准进行换算。

（3）怎么用换算

先找到最适合的面积单位，再把它换算成我们所需要的面积单位。

2、重新定位量感，落实量感

（1）从生活中激发量感 （2）从操作中培养量感 （3）从推理中发展量感 （4）从运用中深化量感

第一稿教学反思

在第一稿的教学中，主要让学生经历了多做操作活动，在操作活动中体验 “量”，并找到量与量之间的关系，再通过想象推理发展到更多的 “量”。从实际效果来看，我们团队对学生进行了后测，从后测中发现：学生对练一练第二题正确率达到 96%，而第四题第二个问，学生的正确率却只有 48%。

以上数据说明了什么呢？我们团队对学生进行了访谈，在访谈中我们了解到：

一、学生已经掌握了换算的方法，但是不知道为什么要换算。比如：给她一块 6 平方分米的纸板，他能快速的估计出它的面积是 6 平方分米，但是你要问他是多少平方厘米？她就会想，我一眼都看出了它的面积是 6 平方分米，我为什么还要知道她是多少平方厘米呢？

二、学生对面积单位的实际体验不够，比如：你要问她门的面积大约是多少，她会很快的告诉你，大约是 2 平方米，但是你要问她，门大约是多少平方分米？大多数学生并不能想到要先想是多少平方米，再换算成平方分米。

三、学生对长度单位的换算非常熟悉，这即是本课的基础，同时也是本课的阻碍。

教学设计（一稿）

一、独立研习、探寻新知

在前面的学习当中，我们认识了面积以及面积单位，老师想让孩子们猜一猜这个正方形的面积是多少呢？（出示一个 1 平方分米的正方形）

预设： 生 1:1 平方分米（大多数学生的答案） 生 2：100 平方厘米 生 3:90 平方厘米 .................

师：感谢孩子们的配合，想要准确的知道这个正方形的面积是多少有什么好的办法吗？

生：量出正方形的边长后再计算。

师：那就请孩子们量一量，算一算吧！（每一个孩子都准备了一个 1 平方分米的正方形）

预设： 生 1：10×10=100 平方厘米（大多数孩子的做法）

生 2:1×1=1 平方分米（少数孩子的做法或者没有这个答案，如果没有这个答案就从学生的才想入手引起置疑）

师：（置疑）有的孩子计算出是 100 平方厘米，而有的孩子计算出是 1 平方分米，那究竟谁计算的是正确的呢？为什么？

预设：生 1: 都是正确的。因为它们所用的单位不同，而实际大小是一样的

生 2: 都坚持自己的答案。

师：如果这两个答案都是正确的，那么我们是不是可以做出这样一种猜想：1 平方分米 = 100 平方厘米。今天这节课我们就一起来研究《面积单位的换算》

二、同伴研讨、探究疑惑

师：为了验证我们的猜想，请孩子们利用老师提供的工具，自己制作一个 1 平方分米的正方形，并说说您有什么发现？

教具一：剪刀一把，方格纸一张（每个小方格边长位 1 厘米）

教具二：100 个面积为 1 平方厘米的小正方形

教具三：白纸一张，铅笔一枝、直尺一只。

说明：每一种教具只提供给一个小组（4 个人），小组合作探究然后汇报。

预设：

教具一

要求：请利用剪刀和方格纸剪出一个 1 平方分米的正方形，并说一说 1 平方分米和 1 平方厘米有什么关系？

生 1: 因为一个小正方形的边长是 1 厘米，数 10 格就是 10 厘米，也就是 1 分米，再数 10 行，就是一个面积为 100 平方厘米，也就是 1 平方分米的正方形。

生 2：通过剪下来的方格纸发现，1 平方分米 = 100 平方厘米。

教具二

要求：利用面积为 1 平方厘米的小正方形拼出一个面积为 1 平方分米的大正方形。并说一说需要多少个？有什么发现？

生 1：一行摆 10 个，摆 10 行，刚好就是一个 1 平方分米的正方形。

生 2：10×10=100 个，也就是说这个正方形的面积也是 100 平方厘米。所以 1 平方分米 = 100 平方厘米。

教具三

要求：请用铅笔和直尺在白纸上画出一个面积为 1 平方分米的正方形，并说一说您是怎么画的，有什么发现？

生 1：因为 1 分米 = 10 厘米，边长为 1 分米的正方形面积为 1 平方分米，10×10=100 平方厘米，所以 1 平方分米 = 100 平方厘米。

师：通过刚才的活动，我们证实了 1 平方分米 = 100 平方厘米，借助刚才的活动经验，你能说一说 1 平方米 =（ ）平方分米吗？

预设：生 1：我们可以把刚才的方格纸想象成边长为 1 分米的正方形，也需要 10 行 10 列，也就是 1 平方米 = 100 平方分米。

生 2：我们可以把小正方形想象成 1 平方分米，需要 10 行，每行 10 个，才能摆出 1 平方米的正方形，所以 1 平方米 = 100 平方分米。

生 3：因为 1 米 = 10 分米，10×10=100 平方分米，所以 1 平方米 = 100 平方分米。

师：孩子们真棒，能够学以致用。

三、团队研述、探索提炼

师：通过猜想、验证，我们得到了这两个结论。老师把他们画成了一幅图，不知道孩子们从图中能看出些什么呢？

预设：生 1：1 平方米 = 100 平方分米

生 2：1 平方分米 = 100 平方厘米

生 3：1 平方米 = 10000 平方厘米

四、练习巩固，拓展提升

1、教材 75 页第 2、4 题。

2、拓展题。

                教学目标

1、经历探索面积单位进率的过程，能用图示等方式解释面积单位的进率，能解决一些简单的实际问题。

2、结合解决问题的情境，体会面积单位换算的必要性，能正确进行面积单位之间的换算。

3、提高推理能力，进一步发展空间观念，培养学生的量感。

                教学重难点

重点：结合实际操作过程，探究面积单位之间的进率。

难点：提高推理能力，发展空间观念，培养量感。

                          学情分析

纵观小学阶段，学生在学习本单元之前，已经学过长度单位以及周长的计算，但这些知识都属于一维的长度，而本单元是学生在小学阶段初次接触的二维的面积，相对于一位的长度，二维的面积更加的抽象，是学生空间认识上的一次飞跃。 纵观本单元来说，本课是第四课的内容，在学习本课之前，学生已经学习了面积的概念、面积单位以及长方形、正方形的面积计算，这些知识这是本课的学习基础。

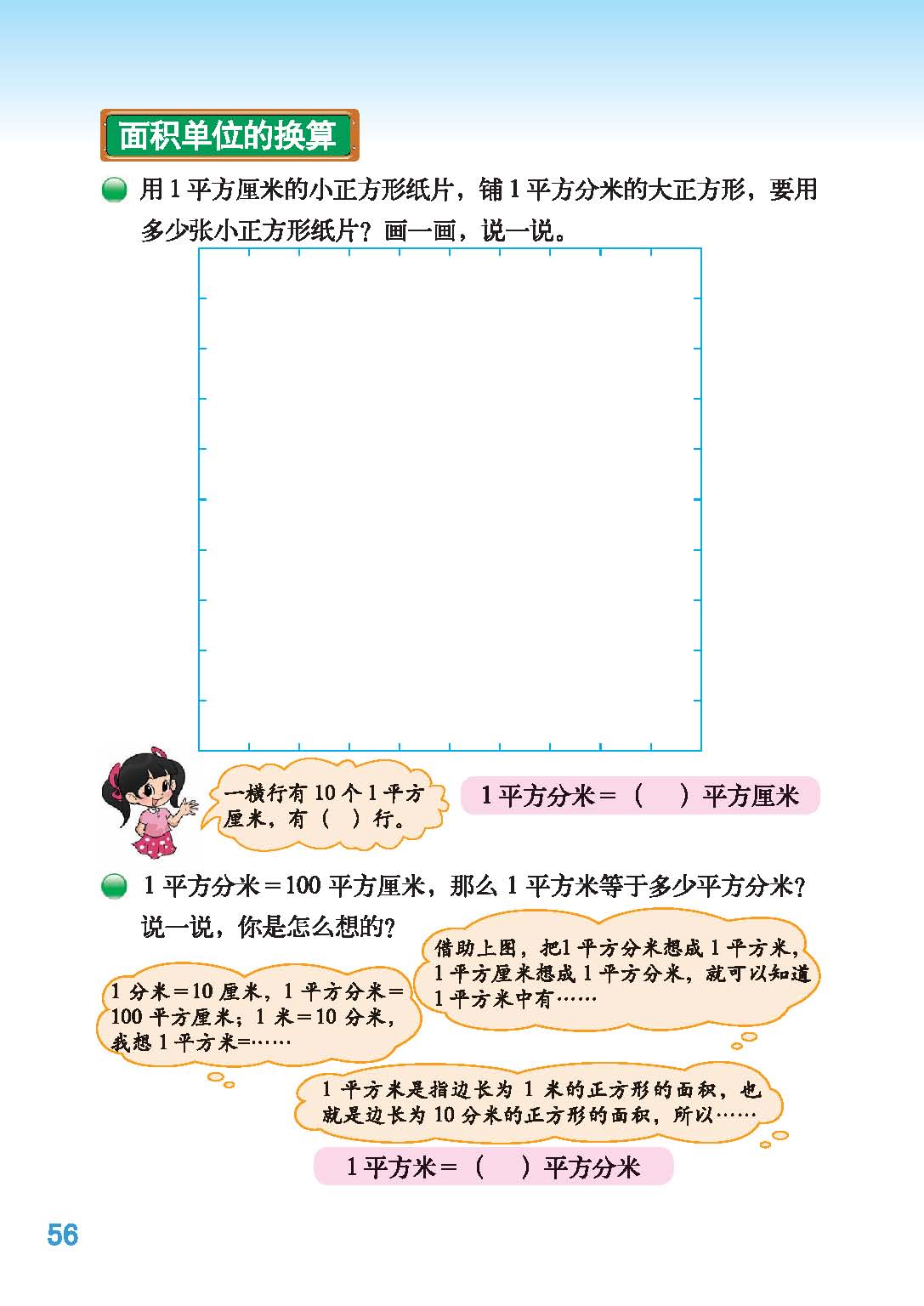
                         教材分析

在本课中，教材呈现出两个问题，第一个问题探究平方分米和平方厘米的关系，教科书呈现了 1 平方分米的正方形，正方形每隔 1 厘米画一个小点，其意图是引导学生通过画图体会平方厘米和平方分米之间的关系：每行有 10 个 1 平方厘米的正方形，有 10 行，因此一共有 100 个 1 平方厘米的小正方形，所以 1 平方分米 = 100 平方厘米。第二个问题通过推理，探究平方米和平方分米之间的关系，学生会借助第一个问题的探究经验，实现知识的迁移。

                          课前思考  

“面积单位的换算” 是北师大版小学数学三年级下册第五单元第四课时的内容，主要的学习内容是探究面积单位的换算，进一步发展空间观念。在这之前，学生已经系统的学习了面积的概念、面积的单位以及长方形和正方形的面积计算方法，这些知识正是本课的学习基础。执教本课，我进行了如下思考：

1、如何触发学生的疑惑？

学生在系统学习面积的单位后，还并不能把面积的单位联系起来，还处于一种比较朦胧的状态，比如在一些数字过大的填写单位的题中，学生出错的比重就比较大，主要原因就是学生还不能实现单位之间的换算，在比如给学生出示一张面积为 1 平方分米的纸片，让学生说一说他的面积是多少？大部分学生会说大约 1 平方分米，再通过学生的实际测量会发现这张纸片的面积是 100 平方厘米，出现了两种结果，它们之间有什么联系呢？把这个疑惑作为本课的触发点。

2、如何带领学生经历 “换算” 的过程？

多年的一线教学经验中，我们发现直接告诉学生 1 平方分米 = 100 平方厘米，再告诉学生转换的方法，学生能解决一些简答的问题吗？我想是能的。但这样的方式明显不利于学生数学思维的建立与发展，因此在本课中，让学生经历 “换算” 的过程就十分必要了，我想让学生经历直观的操作感知，经历知识的产生过程是本课的关键。

3、如何培养学生的量感？

学生的量感，不是靠记忆，而是借助周围熟悉的事物或工具，在学习生活中慢慢形成的。因此，需要教师在教学中尽可能多的提供材料，鼓励学生借助这些材料进行估计和实际操作，从而培养学生的量感。

北师大版三年级下册第五单元《面积单位的换算》教材图片如下：