xyl123新世纪小学数学论坛 第 12048 号会员,加入于 2022-02-08 13:38:56 +08:009 |
| 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》展示大赛-2022 • xyl123 • 4年前 • 最后回复来自 18771778509 | 116 |
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
学习活动单
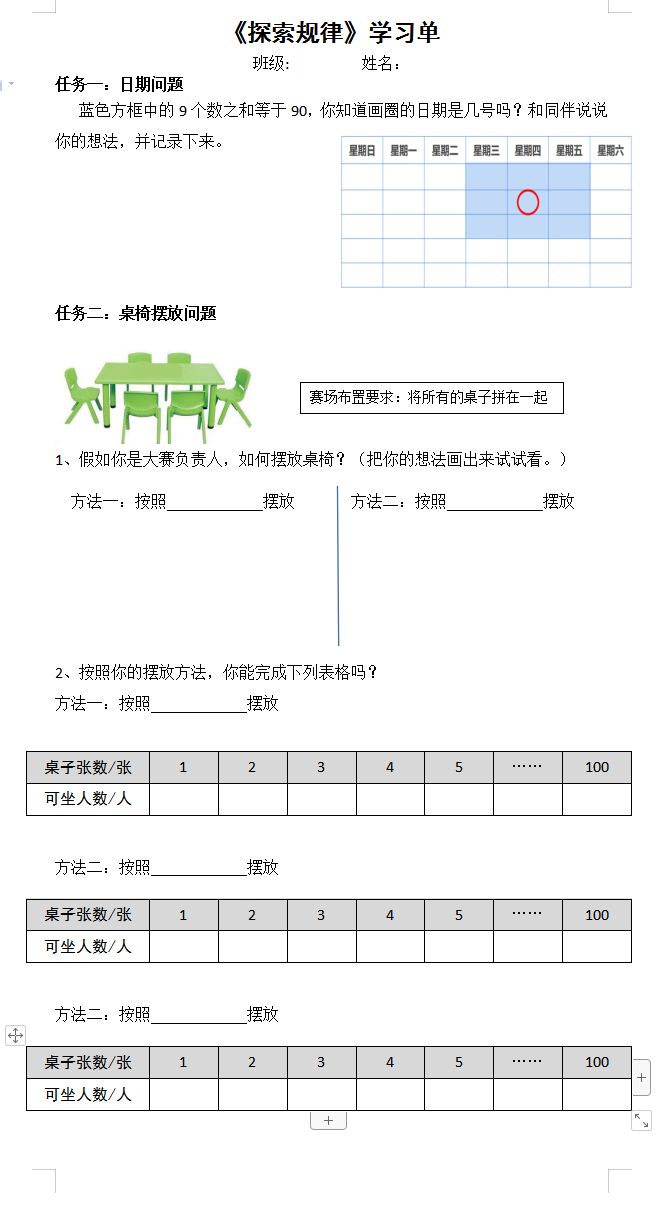

4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
如果不用符号表达会使数学研究陷入泥潭,一方面是很难进行更深入的研究,另一方面是很难进行知识传播。古代中国有过许多重要的数学成果就是因为没有抽象为符号表达,使得这些成果没有得到深入研究,甚至没有得到传承。比如,元代数学家朱世杰(1249——1314),他在 1303 年左右出版了数学著作《四元玉鉴》,这部著作述说了许多高维的数学问题,比如,书中提出的 “四元术” 是一种解多元高次联立方程组的方法。比如书中还提出了 “垛积术” 就是一种从立体层面考虑的三维的级数求和方法。可惜的是,在这部著作中,无论是问题的提出还是结果的描述几乎都是具体的数值,没有抽象成一般的符号表达,因此很难让后人理解问题的本质和解题的思路,因此明清以后就没有人能理解朱世杰的工作了。由此可见,用抽象的符号来表述概念从而形成数学的研究对象,用抽象的符号来表示研究对象之间的关系从而形成命题,对数学是何等重要。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
后来笛卡尔(1596——1650)完成了代数符号的改进工作,用拉丁字母的前几个字母 a、b、c 表示已知量,用 x、y、z 表示未知量,这种方法沿用至今。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
韦达定理。第一个有意识使用字母表示抽象运算的是法国数学家韦达(1540——1603)在韦达之前人们认为像 3+2x=1 和 2+3x=5 这样的两个方程是不一样的。韦达用 a+bx+c=0 的形式一般性地表示一元二次方程,其中 a、b、c 这些字母系数可以表示任何数。借助字母系数,韦达给出了一般的求根公式:这样,对于具体的数字系数,只要代入公式就可以得到解。而这个公式的推导过程如果没有用字母表示数在内的符号系统,会变得异常困难,推导过程的表述更是难上加难,即便写出来也没人看得懂。不仅如此,韦达还借助字母研究了根与系数之间的关系,这样由系数可以得到根,由根也可以推算系数,这个公式就是韦达定理。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
丢番图写了一本书叫《算术》,这本书中研究的主要问题是方程的正整数解,,这本书引发了一个著名的猜想,就是费马大定理。这个定理与勾股定理密切相关,法国数学家费马(1601——1665)把问题推广到一般的 n 次幂的代数等式,并且猜想:对于一般的情况,即 n≥3 时,等式 += 不存在整数解,也就是说,不存在同时为整数的 a、b、c 使得上面的等式成立。因此对这样的一类等式,勾股定理是一个特例。问题是简洁的,结论是清晰的,但证明却是相当困难的。经历了三个多世纪,经过几代数学家的不懈努力,于 1993 年被英国数学家怀尔斯解决,长达 130 页的论文发表于 1995 年。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
古代代数学的顶峰大概是在古希腊数学家丢番图(约公元 250 年)时代。有资料表明,是丢番图首先把抽象的符号引入代数学,他甚至给出了相当于现在和 x 的 3 次以上幂的表现形式,这在当时被认为是极度抽象甚至难以想象的。因为当时的人们普遍认为一个数的 2 次幂是平方、3 次幂是立方,都有具体的几何背景:平面图形面积和立体图形体积,但 3 次以上幂就没有具体的几何背景了,因此认为这样表示是没有意义的。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
虽然符号在我们现在的社会生活中随处可见,无论是自然科学还是社会科学,甚至是人文科学,用符号表示概念、关系、法则已经成为一种常识。但人类真正学会符号表达却是经历了相当漫长的岁月。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
用符号表示分类,不仅能够更加清晰地表达分类,而且能够更加深刻地理解分类的标准,进而能够更加深刻地理解所要研究问题的性质。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
符号意识所蕴含的数学思想是抽象思想。数学学习中最重要的三大思想就是抽象、推理和模型思想。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
在义务教育阶段整个学习过程中,学生用符号表达数学对象是一个由简单到复杂、由相对具体到相对抽象的过程,符号意识的发展是一个逐渐积累变化的过程。小学数学教材中的数学符号是根据小学生的年龄特点、思维特点,有计划、有步骤的引入的。教材在各个年级都安排了用符号表示数的内容。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
使用符号表示变化 (规律),让数学思维严密起来
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
灵活地运用数学符号,可以简明地表达数学思想,简化运算,加快思维的速度,促进思想的交流。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
符号意识是数学课程标准的重要内容。从数学课程标准的的视角出发,符号意识是指学生个体能结合具体的情景正确理解符号所表示的意义、灵活应用符号表述数学对象 (数、数量关系、变化规律)、进行符号运算的一种能力。培养学生的符号意识成为数学教学过程中一项重要的内容。许多学者在不断的丰富对于符号意识的相关理论,数学教师也在不断的更新自己的教学策略。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
探索规律是培养学生符号意识的重要载体。在探索规律过程中,要把规律从具体的情景中抽象出一般的模型,就十分需要借助符号来思考,在教学中要从具体情景中抽象出数量关系和变化规律,体验将问题解决过程符号化的优越性。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
发现规律的 过程是一种探索性的、具有发现或发明性质的活 动,当学生经历初步的探究之后,往往就有了较为 感性的认识,形成了一定的猜想。根据规律建构的 一般原则,猜想必须经过严格的验证,这也就是数 学研究的过程,是多种思维不断完善的过程,也是 科学制度、科学方法逐步形成的过程。在验证过程 中,学生运用已有的知识技能经验,对学习材料进 行研究、实验、实践,并尝试变换角度、形式,重新完 善、修正甚至否定。在这种操作、实践、思辨的过程 中进行验证,在自我肯定或否定中逐步找到数学规 律的实质,最终归纳出合理结论从而来验证自己的 猜想。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
学生对规律探索产生了极大的兴趣,就会积极 地投入到数学探究活动中去,可以自主进行观察、 计算、比较、发现等操作活动,并有意识地从现实的 情境中获得数学信息,并根据得到的数据或现象进 行独立思考,从而做出合理的猜想,感受到数学现 象中隐藏的数学规律。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
心理学研究表明,给定的数学现实或数学学习 材料的质量是影响学生数学学习的主要因素。对 于探索规律而言,学习材料的重要性不言而喻,只 有通过有质量的数学问题驱动才能产生规律探索 的动机和欲望。在教学时一般可以通过三种情况 进行问题驱动:一是现实的生活情境;二是几何形体的情境;三是有趣的计算情境。在创设探索规律的情境时要做到生动有趣,易被学生接受。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
可以看出教科书中 “探索规律” 的学习内容是 力图贴近学生的学习心理的,试图为学生提供丰富 的蕴含规律的现实情境或数学现象,给出探索规律 的基本线索和主要活动环节,意图让学生学会用数 学的方法来研究数学现象,从而准确地把握数学规律。
4年前 回复了 xyl123 创建的主题› 展示大赛-2022 › 【2022 春】湖北省宜昌基地(一) 向玉玲 6 下 总复习《探索规律》 |
具体来讲,“探索规律” 的学习活动一般包括五 大环节:一是识别情境对象,一方面帮助学生回忆 已有的相关知识和经验,另一方面建立后面活动的 观察对象,明确研究的目标;二是做出比较观察,这 是探索规律的核心环节,需要观察对象把注意力放 在对象之间或内部的关系方面,形成一定程度上的猜想与概括;三是主动验证概括,对前期相对零散 的猜想或结论进行实验验证,找到共性,归纳出具 有一定普遍意义的猜想或结论,并对这样的结论或 者猜想的正确性进行实验、解释和证明;四是适度 的应用推广,任何一个规律往往可以链接出更具有 普遍性的规律,因此需要适度培养学生推广与应用 的意识,主动运用规律去进行解释与拓展;五是全 面反思总结,对学习个体探索规律的研究过程进行 反思性回顾,强化对数学思想方法的体悟,或重规 律的理性表达,或重研究的方法内化,意在培养学 生及时反思总结的习惯,逐步培养学生的研究发现 能力。