第 2 稿 :《角的度量（一）》教学设计

四川成都 ・周洪海数学工作室

一、 教学目标

1. 结合生活实例比较角的大小，产生度量角的需要，经历角的度量过程，体会角的度量的本质；感受统一度量标准的必要性，掌握角的度量单位，了解 1° 角实际有多大。

2. 知道直角、平角、周角的度数及其大小关系，并会估测生活中角的大小。

3. 在实践探究量角方法的过程中发现数学规律，体会角的大小在现实生活中的作用。

4. 培养学生的动手操作能力、发现问题和探究解决问题的能力。

二 、教学重难点

重点： 体会角的度量本质，感受统一角的度量标准的必要性。

难点： 经历 1° 的产生过程并感知 1° 角实际有多大。

三 、教学准备

多媒体设备、标准角学具和教具、题单

四 、教学过程

（一）触发

活动 1：情景引入，比较角的大小

师：现在很多小区里都有这样的游乐设施，玩过吗？我这里也有三个滑梯，让你选，最想滑哪个？为什么？

（学生交流）

生 1：第 1 个很平，更安全。

生 2：第 2 个一般，比较舒适。

生 3：我想滑第 3 个，抖坡的，比较刺激。

【设计意图：学生会用生活化的语言描述不同，说明学生对角度有了一定的感知。】

师：为什么滑的时候会有不同的感受呢？

【预设】生：夹角越小，下滑的速度就慢；角度越大，下滑的速度就快。

师：滑梯面与地面形成夹角的大小影响了下滑的速度。如何度量这三个角的大小呢？ （PPT 演示，抽象出角）

活动 2：类比推理，确定量角工具

师： 哪些工具可以度量三个角的大小？ 试一试、量一量。

【拍照收集学生度量作品】

【预设】生 1：用量角器。

生 2：可以用直尺量。

生 3：可以用三角尺的角来量。

（如果学生没有想到用直尺量的这种方法，可以出示方法，让学交流讨论。）

9632

师：还有其他方法吗？

【设计意图：学生思考，当学生遇到困难时，启发学生回顾以前学过的如何测量铅笔有多长和如何测量课桌表面的面积，启发学生通过类比推理，想到：可以找一个 “小角” 作为标准来测量角的大小。】

师：今天我们就以 “标准角” 为测量工具，来研究角的度量。（板书课题）

（二）追究

活动 3：自主探究，达成度量共识

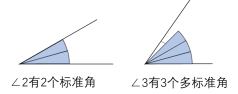
师：老师在学具袋里给大家准备了和∠1 大小一样的标准角。请你用∠1 做 “标准角”，量出：∠2、∠3 分别有几个标准角？

（PPT 出示活动要求，学生自主探究。）

（组织学生汇报交流，拍照上传）

【预设】生 1：∠2 里面刚好有 2 个标准角，但是∠3 里面有 3 个多标准角。

9633

生 2：我们发现，∠2 刚好有两个标准角，但∠3 摆 4 个又多了，摆 3 个又小了。

师：多出来的一部分不满一个 “标准角”，怎么办呢？

【预设】 生：用 ∠1 做 “标准角” 来测量∠3，太大了，得找个更小的标准角。

师：多么有创造力的想法。我们就用一个更小点的标准角来试一试。

（PPT 演示，学生数。）

师：有什么发现？

生 1：还有多的，说明需要更小的标准角。如果还有多的，说明还需要更小小的标准角。

生 2：同一个角，当选取大小不同的角为标准去测量时，结果不一样。

生 3：选取的标准角越小，测量出的结果越精确。

师：你们真是会发现、会创造的孩子。

【通过交流分享，激发学生讨论，如果还有多余的部分是应该怎么办？让学生自发地寻找更小的标准角，达成 “选取的标准角越小，测量出的结果越精确” 这一共识。】

活动 4：交流讨论， 认识 度量单位

师：那是不是标准角越小越好呢？多大角用来做 “标准角” 合适呢？

生 1：我认为越小的标准角越好，会更精确。

生 2：我反对，太小了，要铺很多。还要摆的时候要方便。

师：其实，数学家们也像你们一样，激烈地讨论过用多大的角做 “标准角” 合适。其中最常用的 “标准角”，就是 1 度大小的角。出示资料：把圆平均分成 360 份，其中 1 份所对的角的大小就是 “1 度”，记作：1°。因此 1 度也就成为了最常用的角的度量单位。

师：你能找到 1° 在哪里吗？

（学生在两幅图中找 1°，交流感受。）

师：对呀，小小的 1° 真不好观察。但数 10 个 1° 拼起来，就有感觉了。记作：10°。

师：你还能在图上找到其他的度数的角吗？画一画、标一标。

9634

（学生自主探究、交流汇报。板书学生找的 1 周角、1 平角、1 直角等。）

<跳转至下一楼层，继续查看>