【学习过程】

一、探究新知

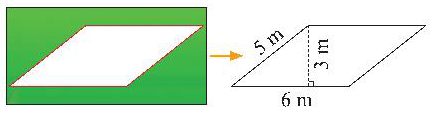
如图，公园准备在一块平行四边形的空地上铺上草坪。

9048

（一）活动一：如何求这块空地的面积？说一说你的想法和理由。

1. 准确描述数学信息。

问题 1：仔细观察情境图，描述这块平行四边形空地的数据？

预设：

生：这块平行四边形空地的底边长 6 米，斜边长 5 米，高 3 米。

2. 想一想，说一说

问题 2：如何求这块空地的面积？

预设：

生 1：底边乘斜边；长方形的面积是长乘宽，平行四边形的面积可以是两条临边长度相乘；

生 2：底乘高；

生 3：可以借助方格纸来数一数；

【设计意图】：结合铺草坪的情境，将生活问题数学化，激活学生对于平行四边形的认知经验，引发学生思考如何求平行四边形面积，为接下来的深入探究埋下伏笔。

（二）活动二：借助方格纸数一数，比一比。

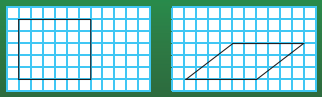
1. 出示长方形、平行四边形的方格图

9049

问题 1：数一数，比一比，你有什么发现？

预设

生 1：长方形的面积是 5×6=30。

生 2：平行四边形所占的小方格肯定不够 30 个。

追问：通过比较，请大家大胆猜想一下，这个平行四边形的面积可能与它的什么有关？

预设

生 1：底。

生 2：与底和高有关，与斜边无关。

小结： 通过借助方格纸，我们能够 “数” 出平行四边形的面积，它与长方形的面积计算方法并不通用。同时，我们还猜想得出平行四边形的面积与它的底和高有关。

【设计意图】：通过数一数，比一比，让学生体会借助方格纸能够 “数” 出图形的面积。得出平行四边形与长方形的面积计算方法并不相同。引导学生发现这个平行四边形的面积与底和高有关，与斜边无关。

（三）活动三：你能把平行四边形转化成长方形吗？

虽然与长方形的面积计算方法并不相同，但是平行四边形与长方形却有着密切的联系。如果能把平行四边形转化为长方形，是不是就很容易求出它的面积了呢？

问题一：你能把平行四边形能转化成长方形吗？

1. 思考、操作、验证

学生利用学具独立操作。

2. 四人小组交流展示

学生组内展示交流方法和收获。

3. 全班汇报评价

学生上台展示

预设

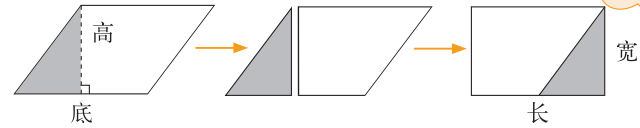
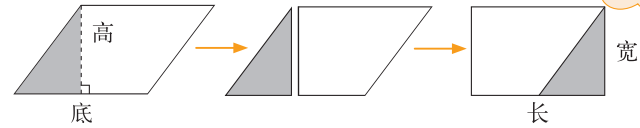
沿平行四边形的一条高线剪开之后进行拼接，能够得到一个长方形。

9050

问题二：拼成的长方形与原来的平行四边形的面积有什么关系？

预设

形状变了，面积没有变。

【设计意图】：让学生通过独立操作进行实验探索，理清将平行四边形转化为长方形的过程与方法，把实践操作与想象思考相结合，促进学生想象分析水平的提高，在交流和分享中获得知识与经验，发展空间观念。

（四）活动四：怎样求平行四边形的面积？想一想，并与同伴交流。

1. 结合实验操作，独立完成作业单。

9051

9052

2. 组内交流。

3. 汇报收获。

平行四边形通过转化得到了长方形。平行四边形的底相当于长方形的长，平行四边形的高相当于长方形的宽，长方形的面积等于长乘宽，由此能够得出平行四边形的面积等于底乘高。

【设计意图】：通过动手操作，用割补的方法把平行四边形转化成长方形，找出两个图形之间的联系，推导平行四边形的面积公式。在动手操作、合作学习的方式，让学生经历自主探索的过程。

二、拓展练习

9046

9047

三 全课总结

学完本节课，你有哪些收获？