且行且思考

——《面积与周长的比较》教学设计综述

“路漫漫兮其修远，吾将上下而求索”。面对新教材，面对实践过程中的困惑，我们有太多的问题需要探讨和交流。感谢新世纪小学数学为我们提供了这个宝贵的平台，这样开放式的探讨，且让我们在实践的过程中，有了与同行更多的交流机会，让我们的思想在不断碰撞的过程中，能够深入进行思考、研究，能够不断突破、进步。

在这次活动中，关于读懂教材，我有了很深的体会：

首先，就是对学习目标的思考。目标是一节课的灵魂，恰当地把握目标是数学教学的关键。

本节课在探究周长和面积与正方形边长的倍数关系上，我就遇到了目标把握错误的尴尬。（教学设计如下所示：）

4911

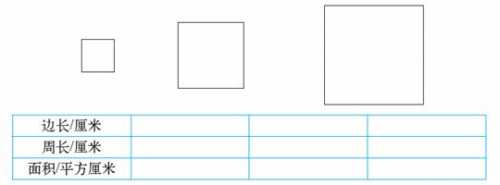
课堂上学生通过计算、观察，发现：（箭头）

正方形的边长乘 2，周长也乘 2，面积乘 4，也就是（2×2）；

正方形的边长乘 3，周长也乘 3，面积乘 9，也就是（3×3）；

由此猜测结论：如果用 n 表示正方形边长所乘的数

正方形边长乘 n，周长也乘 n，面积乘 n×n.（板书）

验证猜测：

过渡：是不是正方形的边长乘所有的数，都有这样的规律呢？

我们来验证一下！（课件补充表格）

边长乘 5，是 5 厘米，周长就是 20 厘米，面积是 25 平方厘米。

边长乘 10，是 10 厘米，周长就是 40 厘米，面积是 100 平方厘米

边长乘 100，是 100 厘米，周长就是 400 厘米，面积是 10000 平方厘米

……

总结讨论：

那你说，大臣这样分土地公平吗？为什么？

（生：多了一个人，面积却大了好多！）

这样的设计我是这样考虑的： 前测时，在毫无提示情况下我找了两个同学试做，学生对解决这道题没有太大障碍，我就在想，这道题的意图是什么，学生对这道题要掌握到何种程度就行了？能不能拓展？用字母表示数确实学生还没有学习，但我想，这应该不难理解，就拓展一下吧，上课时我引入 n 来表示规律，课堂上有三分之一学生经过我简单介绍能明白什么意思，但确实有不少学生存有疑惑。

在讨论中，古荥小学刘双枝、王和平两位老师也在帖子中提到：探究周长面积与边长变化的倍数关系中的活动，“计算观察发现规律”，边长乘 2，周长乘 2，面积则乘 4（2 乘 2），……（3 乘 3）……，然后用字母 n 来表示规律，总感觉对于三年级的学生，理性的知识太强，难度很大。

所以，我在下一稿的设计中就删除了这一环节，回头想想，这样的错误恰恰就是我 错误理解了本题目标，盲目拔高了目标的结果。

第二，是对教材内容的思考。 这点我也犯了一个愚蠢的错误： 初次看到教材后，心想， 这么多的练习题，显然不是一课时，于是我就开始挑选我认为能说明问题的题目进行构思。以这道同时涉及周长与面积的题目来直接引入课题， 4912 引发学生思考， 旨在让学生通过解题来明确分辨出周长与面积在意义、计算方法和计量单位三方面的区别。

而后，我挑选了一道探究性的题目，旨在让学生通过不同方式、不同层面深入体会到面积与周长的不同。

接着，我又从练习中找到两道同时涉及周长与面积的题目，想以此来检测学生对这节课学习的掌握。

后来一想，不对啊，既然不是两课时，那一节课的内容就这样随意挑来挑去？教材是什么意图？ 带着疑问，我又再次审视了教材，根据帖子中侯老师的回复 “练习四这么多内容，可以看出至少需要 2 课时完成，第一课时是基础练习，第二课时可以围绕后面 3 个活动进行展开，在这个过程中，要关注学生数学思考（问题的思考、梳理、展示、交流、反思）和活动经验的积累。” 给了我很大启发，再次修改，我就紧紧围绕第二课时 3 个活动为内容进行设计。