《正比例》教学设计三稿

【教材分析】

《正比例》第一课时，教材首先呈现了正方形面积与边长、周长与边长的表格，通过实例让学生看到每一组中的两种量的变化情况，引导学生初步发现 “正方形的面积和周长都是随着边长的增加而增加”；再通过对比这两组量的变化的区别，从变化中看到 “不变”，初步体会周长与边长、面积与边长之间的变化规律不同。然后再结合 “路程与时间” 两个变量关系的研究，丰富学生认识正比例的例证，初步理解正比例的意义。在第一课时两个正例一个反例的基础上，“试一试” 中又提供了一正一反两个情境，帮助学生辨析理解正比例的意义。这样，教材从不同的角度提供了有利于学生探索并理解正比例意义的情境，既包括 “时间与路程”“乐乐和爸爸年龄变化情况” 等生活情境，也包括 “正方形周长与边长、面积与边长” 等数学情境，情境中有正例也有反例，为学生理解 “正比例” 意义提供了丰富的直观背景和具体案例，以引导学生经历从具体情境中抽象概括出正比例的过程，从而理解正比例的意义。

【学情分析】

前测内容： 正比例第一课时前测题

1. 观察下面表格，写写你的发现。

发现一：

表格 1 中的变化的量有（ ）和（ ），它们是怎样变化的？

表格 2 中的变化的量有（ ）和（ ），它们是怎样变化的？

发现二 ： 表格 1 和表格 2 的两组变量在变化中的相同之处与不同之处是什么？

发现三 ： 你能用自己喜欢的方式表达表格 1 的变化规律吗？

设计意图：

发现一：衔接《变化的量》后测，学生借助表格用自己的语言分别描述两表中的变量关系。

发现二：观察学生学习路径，对比表 1 和表 2 观测学生做对比时，运用生活化语言关注表象不同、还是能运用数学语言、符号语言关注本质规律。

发现三：学生在表征变化关系时，观测学生符号意识思维水平处于经验观察水平、本质内化水平、理性辩证水平、结构普适水平哪一水平。

知识基础：

《正比例》这个内容是学生在学习乘法时，已经初步接触了正比例的变化规律，在六年级上册已经学习了比的意义、比的化简与比的应用等。

学习难点：

判断有具体数据的两个量是否成正比例是学生容易掌握的，但是离开具体数据，判断两个量是否成正比例对学生来说是有难度的。

【教学目标】

1．结合 “正方形的周长与边长，正方形的面积与边长，路程、时间与速度” 等情境，用自己的语言描述它们之间的变化关系，能从变化中看到 “不变”，认识正比例。

2．能根据图表或文字总结成正比例量的变化规律，并用此规律判断两个相关联的量是不是成正比例，能举出生活中成正比例的实例。

【教学重难点】

教学重点：

经历从具体情境中抽象概括出正比例的过程，理解正比例的意义

教学难点：

体会 “变与不变” 的数学思想，运用运动和变化的观点、集合和对应的思想分析变量关系，依据正比例的意义判断两个量能否构成正比例关系。

【教学过程】

一．情境导入，探究两个变量间的关系

师：同学们， 第二单元我们学习了比例的相关知识， 上节课我们认识了，生活中有许多变化的量，今天我们继续跟随淘气、笑笑走进变量的世界。

呈现视频动画，引出问题： 正方形周长与边长，面积与边长是否存在着某种关系。

探究要求：

1. 独立填写表格。

预设：

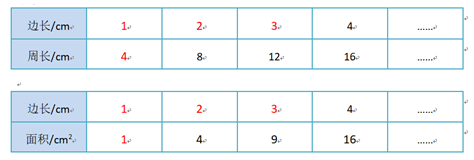
师追问：边长 4cm 吗？只能是整数吗？如果边长是 3.5cm，周长和面积是多少呢？

预设：

生 1：边长还可以是 5、6、7...... 一直增长，同样周长和面积也很会随着增长

生 2：边长也可以是小数、分数，但都比前面的 3 大

生 3: 当边长是 3.5cm 时，周长时 3.5×4=14cm，面积是 3.5×3.5=12.25cm²

【调整理由：表格中数据的补充，学生更多的是借助过去所学数量关系，关注点多在计算，没能站在动态的、对应的角度去看看待变化关系。由学生习惯的常量视角到变量视角的变化，需要老师引导学生调整观察视角】

2. 小组合作探究：观察表格你有什么发现。

预设：

生 1：正方形的周长总是边长的 4 倍。

生 2：正方形的周长与边长的比值是一样的。

生 3：正方形边长加 1cm，周长就增加 4cm。

生 4：正方形边长扩大几倍，周长就扩大几倍。

生 5：正方形的面积和正方形的周长都随着正方形的边长增加而增加。所以正方形周长与边长，面积与边长是相关联的变量。

调整：

师追问：同学们的观察发现有横向、纵向，我们一起梳理一下：从左到右看正方形的面积和周长都随着正方形的边长增加而增加，那从右到左呢？他们的关系怎么表述。

预设：

生 1：从右到左看正方形的面积和周长都随着正方形的边长减少而减少。

生 2：我们可以说正方形的面积和周长都随着正方形的边长变化而变化，而且它们的变化方向是一致的。

【设计意图：借助学生熟悉的正方形周长与边长，面积与边长这两种学生熟悉的相关联的量， 通过引导学生有序观察，梳理自己的发现， 让学生感知判断正比例关系的第一个要素，两种量相关联，一个量随着另一个量的变化而变化 （变化方向一致）。】

二．比较变量特征，认识正比例

（一）情境一：正方形周长与边长，面积与边长变量关系的不同特点

师：同学们发现了上面两种变量关系的共同点是：

都是相关联的量，一个量随着另一个量变化而变化。（方向一致）

追问：那么正方形周长与边长，面积与边长的变化规律相同吗？

预设：

生 1：正方形的周长是边长的四倍，但面积与边长的倍数关系是不确定的。

生 2：正方形周长与边长的比值是不变的，但面积与边长的比值是不相等的。

师：能用更简明的数量关系式表示它们的变化规律吗？

预设：

生 3： 正方形的周长 ÷ 正方形的边长 = 4（一定）

正方形的面积长 ÷ 正方形的边长 = 正方形的边长（变化的）

【设计意图：在学生发现两组量的变化情况的基础上，引导学生发现两组变量变化规律的不同，从变化中发现不变为理解正比例意义奠定基础，并引导学生用更简明的数量关系式表征关系。】

（二）情境二：一辆匀速行驶的汽车，行驶时间和路程

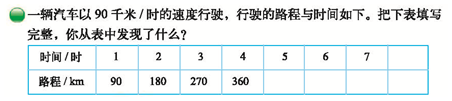
独立探究要求：

1. 独立完成表格，观察表格想想你从表中发现了什么。

3. 变化有什么规律，并用数量关系式表示。

预设：

1. 学生独立填写表格

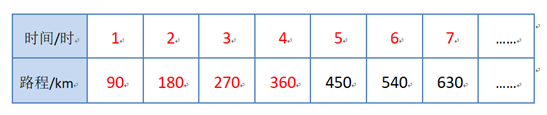
生 1：时间还会一直增长，路程也会随着时间增加而增加，如果用字母 n 表示时间，路程就是 90n

2. 说一说你的发现。

生 1：时间是原来的几倍，路程也是原来的几倍。

生 2：时间是原来的几分之一，路程也是原来的几分之一。

3. 变化有什么规律，并用关系式表示。

生 3：速度 × 时间 = 90（速度一定）

生 4：90× 时间 = 路程

追问：90 这个比值表示什么意义呢？

生：表示速度，速度一定就是匀速行驶。

【设计意图：借助现实世界中学生最熟悉的路程、时间与速度之间的数量关系，速度不变，就是路程随着时间变化而变化的过程中，路程与时间的比值保持不变，由此引入路程与时间成正比例，为学生理解正比例丰富实力支撑。】

（三）对比正比例的材料，说一说什么样的两个量成正比例关系。

师：同学们的发现真精彩，出示正比例的描述性定义。你能说说判断路程和时间是否成正比例的依据有哪些吗？

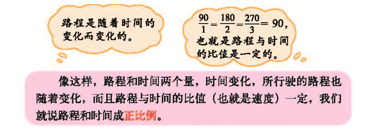
预设:

生 1：路程随着时间变化而变化，它们的变化方向是一致的。

生 2：路程与时间的比，也就是速度是一定的。

师：你能说说第一个问题中正方形周长与边长，面积与边长成正比例吗？

预设：

生 1：正方形周长与边长成正比例，它们是两个相关联的量，且比值一定。

生 2：正方形的面积与边长不成正比例，虽然他们是两个相关联的量，一个量随另一个量的变化而变化，但它们的比值是不确定的。

师：结合正方形周长与边长，一辆匀速行驶的汽车，路程与时间的关系，说一说什么样的两个量成正比例关系。

生：我明白了，两个相关联的量，一个量随着另一个量的变化而变化（变化方向一致），且它们的比值一定，它们就成正比例。（板书正比例的意义）

追问：能用一个关系式表示出所有成正比例的变量关系吗？

预设：

生 1：可以用字母表示

生 2：比如 a÷b=c (c 一定) a 可以表示路程或者总价，b 可以表示时间或者数量…，c 表示它们的比值，c 是一定的。

生 3：也可以是 a=bc (c 一定)

追问：这两个式子 a÷b=c (c 一定)， a=bc (c 一定) 都可以表示正比例关系吗？你能说说吗？

生 4：这两个式子 a÷b=c (c 一定)， a=bc (c 一定) 这两个式子都可以表示正比例关系，都能表示 a 随着 b 的变化而变化且比值 c 是一定的。

生 5：它们是乘除法的逆运算，可以互相转化。

【设计意图：让学生自主阅读教科书中给出关于正比例的具体情境的描述性定义。并结合教材中提供的两个正例和一个反例，帮助学生认识正比例的意义】

三．巩固练习，辨别生活中的正比例关系

1. 学校科学小组在同一时间、同一地点进行观察实 验，测得竹竿的高与竿影的长如下表。

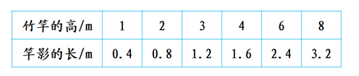
（调整）

（1）表格中相关联的量是（ ）和（ ），（ ）随着（ ）的变化而变化。

（2）写出几组竿影的长与竹竿高的比，并计算比值（比值表示什么），你的发现了什么？

我的发现：

（3）竹竿的高与竹影的长是不是成正比例？ 说明理由。

【设计意图：考察学生能否依据正比例的意义判断两个量是否成正比例，学生不仅要写出结论，还要说明理由。学生用自己语言描述的过程，就是对正比例意义应用过程。 学生对正比例的不同呈现方式，判断的难易程度是不同的，其中表格法呈现的判断正确率高于纯文字描述的呈现方式，可见学生还是需要借助直观性强的素材理解正比例的意义。第一题基础训练中，以表格数据为载体呈现变量关系，以引导式的问题，帮助学生有序思考、判断正比例关系。】

2. 观察视频中的情境，思考以下的问题

（1）在上面的情境中相关联的量是（ ）和（ ）。（ ）随着（ ）的变化而变化。

（2）情境中两个变化的量成正比例吗？说明理由

追问：你能用字母式解释它们的关系吗？

【设计意图：以加油的动态生活素材，让学生运用运动和变化的观点分析变量关系，用字母式概括表示出，金额和油量所有点的集合及其对应关系。 脱离表格数据呈现变量关系，是学生厘清正比例的难点，以学生熟悉的加油情境的动态视频，让学生在变化中思考，把静态的、有限的表格数据换成动态的、对应的视频数据，引导学生通过分析情境变量关系，而不是只依靠具体数据计算判断正比例。】

3. 联想生活场景，判断两个相关联的量是否成正比例，说明理由。

对比四组变量的变化情况，你能分分类吗？

生活场景一：

一个生产防护服的车间，要生产 10000 件防护服，已经生产的防护服件数与未生产的防护服件数。

生活场景二：

一个生产防护服的车间，要生产 10000 件防护服，每天生产的防护服件数与生产的天数。

生活场景三：

一个生产防护服的车间，每小时生产的防护服为 600 件，生产的防护服的总件数与生产的时间。

生活场景四：

张师傅比李师傅每小时多做 50 个口罩，生产时间相同的情况下，张师傅生产口罩的数量与李师傅生产口罩的数量。

调整： 在同一情境下，设计四个场景，不同的变量， 相同之处都是一个量的变化引起另一个量的变化，但变化趋势是有所不同的： 场景 1、2 两组变量的 变化趋势相反 ，场景 3、4 两组变量的 变化趋势相同 。 相同之处都有变化规律，但是规律却不同： 有和一定，有积一定，有差一定，有比值一定 ，只有比值一定才是正比例，对比之后，学生对于正比例理解更深入。

场景 1 是防护服的总量不变，已生产的和未生产的和一定。

场景 2 是防护服的总量不变，每天生产的防护服件数与生产的天数的积一定。

场景 3 每小时生产的防护服不变，每天生产的防护服件数与生产的天数的比值一定。

场景 4 两位师傅生产口罩的差一定

【设计意图： 在同一情境下，设计四个场景 ，都是相关联的量但变化的趋势不同，都是有变化规律的但规律却不同。让学生在丰富的变量素材中，辨别变量中的关系，通过正、反素材分类对比，进一步强化了正比例的认识。 正、反比例的学习是抽象的，文字描述的呈现更进一步让学生把对数据的关注，提升到对变量关系的关注上，也是学习正、反比例以及后续函数学习的焦点，也是从常量思维到变量思维的转变，给孩子们提供丰富的变量关系，在辨析不同变量关系的本质规律中，进一步加深对正比例意义的理解。】

四．说一说这节课你有什么收获和困惑

五．板书

板书的设计还在修改中，想以思维导图的方式引导学生梳理正比例建构的过程，并连贯前后知识形成正比例学习的思维路径，为学生后续自我探究反比例的提供学习路径。