李德毅新世纪小学数学论坛 第 3755 号会员,加入于 2021-03-07 09:17:54 +08:0010 |
| 【2021 春】辽宁大连基地李德毅五下《长方体的体积》展示大赛-2021 • 李德毅 • 5年前 • 最后回复来自 李英 | 63 |
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |
《长方体的体积》学生学习单
探究活动要求:
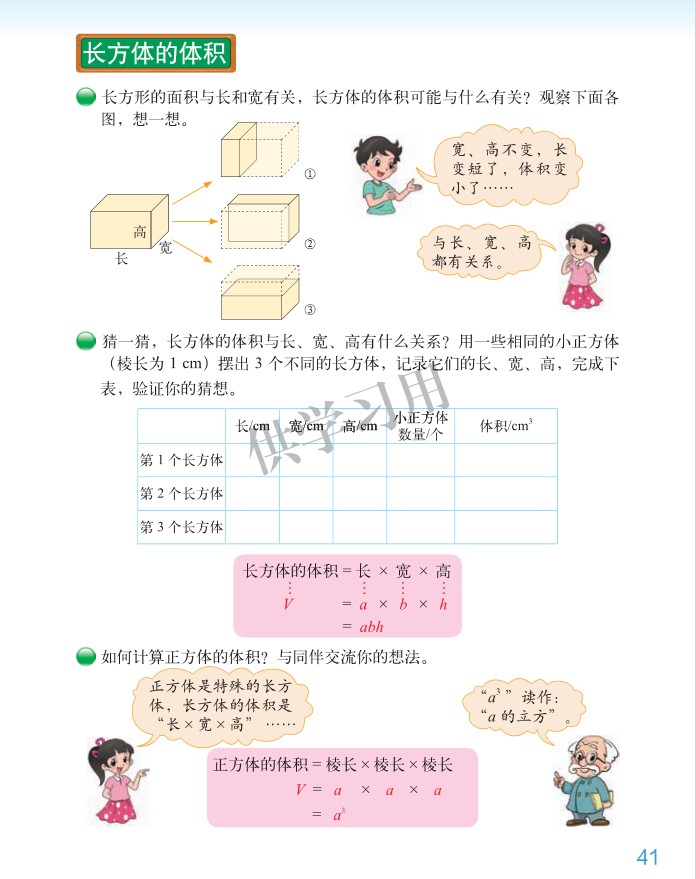
(1)用一些相同的小正方体(棱长为 1cm)摆出 3 个不同的长方体,记录它们的长、宽、高。
(2)同桌合作完成,一个人摆,另一个人记录数据并完成表格。
(3)观察、分析表格,同桌交流,验证你们的猜想(或结论)。
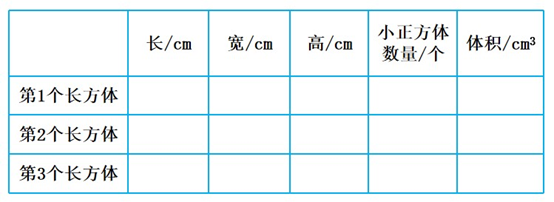
我发现:( )
解决问题: 牙膏盒和魔方,谁的体积大?
练一练 —— 我说你做
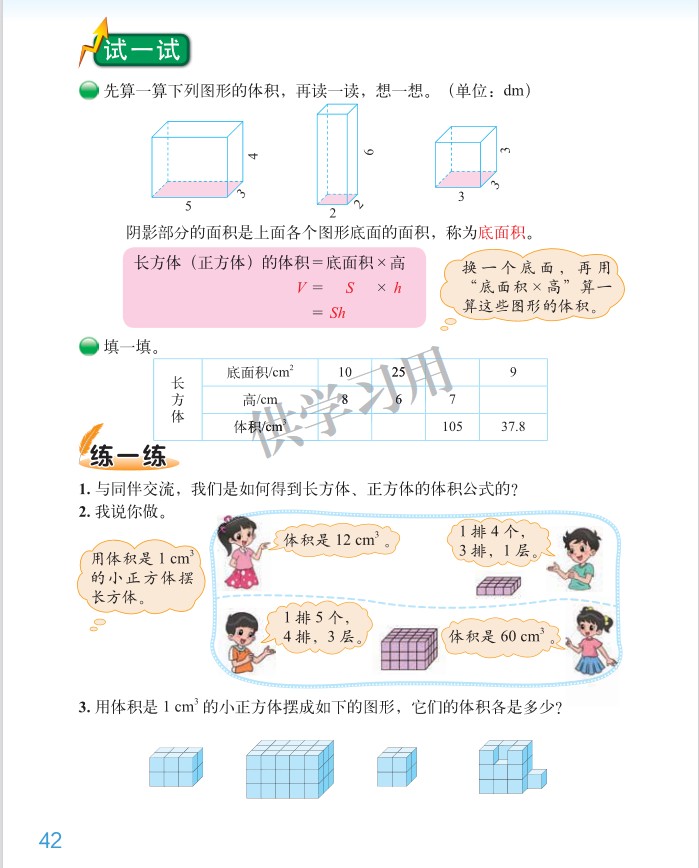
练一练: 用体积是 1cm³ 的小正方体摆成如下的图形,它们的体积各是多少?
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |
《长方体的体积》(第一课时)教学设计 终稿
【教学内容】北师大版五年级下册第四单元 P41 P42 练一练 1-3
【教材分析】长方体、正方体是最基本的立体图形,是研究其他立体图形的基础,长方体、正方体体积的计算,是学生形成体积概念、掌握体积的计量单位和计算各种几何形体体积的基础。教科书重视引导学生经历知识的探究过程。首先安排了长方体体积与长方形面积的类比,启发学生猜测长方体的体积可能与长、宽、高有关;接着安排操作活动,引导学生用小正方体摆 3 个不同的长方体,并记录相关数据。通过观察、分析数据,逐步归纳得出长方体体积的计算方法。最后是自主探索正方体体积计算公式。
【学情分析】学生在第一学段直观地认识了长方体、正方体,并已经学习了长方形、正方形等平面图形以及它们周长和面积的计算。在本册的第二单元,学生学习了长方体、正方体的特征及表面积。在第四单元,学生学习了体积和容积、体积单位。
【学习目标】
1.结合具体情境和实践活动,探索并掌握长方体、正方体体积的计算方法;能正确计算长方体和正方体的体积;
2.培养学生动手操作、抽象概括、归纳推理的能力;发展空间观念;
3.激发学生学习数学、探究数学的兴趣;学会与人合作;学会倾听与质疑,养成独立思考的习惯。
【教学重点】
理解长方体体积公式的的推导过程,掌握长方体、正方体体积的计算方法。
【教学难点】
理解长方体的体积公式的推导过程。
【学习过程】
一、创设情境,体会体积计算方法的重要性
师:(出示牙膏盒和魔方) 同学,这是什么图形?它们正在为 “谁的体积大” 而争吵,你们能帮忙评判一下吗?
【预设】生:这怎么比较呀?得先求出它们的体积。
生:我想到了,把长方体和正方体分割成体积为 1 立方厘米的小正方体,分别数出小正方体的个数,就能比较它们的体积啦
生:你这个想法挺好,就是操作起来太麻烦了!而且在实际生活中,很多情况下,往往是不能用切割的方法来求长方体和正方体的体积的。
生:那怎么办?要是求长方体、正方体的体积,也能像求它们的表面积一样有计算方法就好了!
师:我们先来研究长方体的体积。(板贴课题)
【设计意图】创设情境,激发学生学习数学、探究数学的兴趣。
二、探索长方体、正方体体积的计算方法
师:长方体的体积可能与什么有关?
【预设】生:长方形的面积与长和宽有关,我猜长方体的体积可能与长、宽和高有关。
师:我们结合图形来看看。PPT 长方体的宽和高不变,长减小一些,体积就变小了;长增大一些,体积就变大了。说明,体积和长有关。
生:长方体的长和高不变,宽增加,体积也随着增加;如果宽减少,体积也随着减少。说明,体积和宽有关。
生:长方体的长和宽不变,高增加,体积也随着增加;如果高减少,体积也随着减少。说明,体积和高有关。
生:长方体的长、宽、高越大,长方体的体积就越大;长方体的长、宽、高越小,长方体的体积就越小。
师:你们猜对了,长方体的体积果然与长、宽、高都有关系。那到底有什么关系?
【预设】生:长方形面积 = 长 × 宽,所以我猜,长方体的体积 = 长 × 宽 × 高
生:我通过预习,知道长方体的体积就是等于长 × 宽 × 高
师:长方体的体积是不是等于长 × 宽 × 高,让我们通过实验来验证一下(出示活动要求)用一些棱长为 1 厘米的小正方体摆出 3 个不同的长方体,记录它们的长、宽、高,完成下表,开始实验吧
【预设】生:我每排摆 3 个,摆 2 排,摆 2 层。我摆的这个长方体的长是 3 厘米,宽是 2 厘米,高是 2 厘米,共用了 12 个小正方体,长方体体积是 12 立方厘米。
生:我每排摆 5 个,摆 1 排,摆 3 层。我摆的这个长方体的长是 5 厘米,宽是 1 厘米,高是 3 厘米,共用了 15 个小正方体,长方体体积是 15 立方厘米。
生:我每排摆 4 个,摆 3 排,摆 2 层。我摆的这个长方体的长是 4 厘米,宽是 3 厘米,高是 2 厘米,共用了 24 个小正方体,长方体体积是 24 立方厘米。
生:这是我们整理的表格!棱长为 1 厘米的小正方体,体积是 1 立方厘米。摆这个长方体用了多少个小正方体,长方体的体积就是多少立方厘米。也就是说,长方体的体积等于体积单位小正方体的个数。这两列数据是相等的。
生:你们看,每排的个数 × 每层的排数,等于每层小正方体的个数,再 × 层数,正好等于小正方体的个数。
生:每排小正方体的个数,就是长方体的长。每层的排数,就是长方体的宽。层数,就是长方体的高。那不就相当于长 × 宽 × 高就等于小正方体的个数了嘛!
生:长 × 宽 × 高等于小正方体的个数,也就等于长方体的体积喽!所以长方体的体积真的等于 长 × 宽 × 高!
师:通过操作,我们发现长方体的体积等于体积单位小正方体的个数;小正方体的个数 = 每排的个数 × 每层的排数 × 层数;每排小正方体的个数,就是长方体的长;每层的排数,就是长方体的宽;层数,就是长方体的高;长方体的体积等于 长 × 宽 × 高(出示)。长方体体积公式可以用字母来表示。体积用 V 表示,长用 a 表示,宽用 b 表示,高用 h 表示, V=a×b×h=abh(在这里,乘号可以省略不写)。
师:同学们,请你说说,我们是如何得到长方体体积公式的?
【设计意图】 结合实践活动,让学生探索长方体体积的计算方法;培养学生动手操作、抽象概括、归纳推理的能力,进一步发展空间观念;学会与人合作,学会倾听与质疑。
师:长方体的体积我们会计算了(举牙膏盒),接着再研究什么问题?【问题三】
【预设】生:研究正方体的体积。
师:如何计算正方体的体积?和同桌交流一下你的想法。
生:我是这样想的,因为正方体是特殊的长方体,长方体的体积 = 长 × 宽 × 高,所以正方体的体积也等于 长 × 宽 × 高,正方体的长、宽、高都相等,也就是正方体的棱长。所以正方体的体积 = 棱长 × 棱长 × 棱长。
师:让我们动手摆一摆,验证这个结论。
师:正方体体积公式也可以用字母来表示。
【预设】生:我知道,体积用 V 表示,棱长用 a 表示,正方体的体积公式用字母表示是 V=a×a×a = a³
师:这里 a³ 读作 a 的立方或 a 的三次方,表示 3 个 a 相乘。
师:同学们,请你说说,我们是如何得到正方体体积公式的?
【设计意图】 鼓励学生借助正方体与长方体的关系,通过推理得出正方体的体积公式。
三、掌握计算方法,解决简单的实际问题
- 师:同学们,现在你知道它们谁的体积大了吗?
【预设】生:我想用今天学到的计算方法,但是不知道长、宽、高和棱长是多少,就不能计算呀。
师:是的,要求长方体的体积必须知道?(长、宽、高)。要求正方体的体积必须知道?(棱长)。(学生测量数据,取整厘米) 同学们,请你算一算,比比它们谁的体积大?
生:6×6×6=216cm³ 24×5×5=600cm³ 600cm³>216cm³ 答:牙膏盒的体积大。
【小结】师:你们真了不起,通过猜想、实验、验证、总结出了长方体正方体的体积计算公式,并运用公式解决了实际问题。老师希望你们今后都能用这种方法来学习数学。 同学们,这些知识你们掌握了吗?我们一起来巩固练习一下。
- 课件出示 P42 - 练一练 2
师:我说你做(摆),用体积是 1 立方厘米的小正方体摆长方体。1 排 4 个,3 排,2 层(PPT 出示数据提示),请你搭出这个长方体,并算出体积是多少?(学生先搭后算)
【预设】生:我来出题,每排摆 5 个,摆 2 排,摆 2 层。
师:我再来出题,这个长方体的体积是 16 立方厘米(PPT 提示),你能搭出这个长方体吗?(学生搭)
【预设】生:我每排摆 4 个,摆 4 排,摆 1 层。我摆的这个长方体的长是 4 厘米,宽是 4 厘米,高是 1 厘米,4×4×1=16cm³。 每排摆 2 个,摆 2 排,摆 4 层。我摆的这个长方体的长是 2 厘米,宽是 2 厘米,高是 4 厘米,2×2×4=16cm³。
同桌交流反馈
师:你发现了什么?体积相等的图形,摆法不同,形状也是不同的。
- 课件出示 P42 - 练一练 3
师:用体积是 1 立方厘米的小正方体摆成如下的图形,它们的体积各是多少?
【预设】生:我先观察,这个长方体的长是 3 厘米,宽是 2 厘米,高是 2 厘米,长方体体积 = 长 × 宽 × 高,所以列式 3×2×2=12cm³。
生:这个长方体的长是 5 厘米,宽是 3 厘米,高是 3 厘米,长方体体积 = 长 × 宽 × 高,所以列式 5×3×3=45cm³。
生:我先观察,这是正方体,它的棱长是 2 厘米,正方体体积 = 棱长 × 棱长 × 棱长,所以列式 2×2×2=8cm³。
生:最后这道题,怎样算呢?
生:我是用 “数一数” 的方法,我数了一下,一共有 18 个小正方体,所以体积是 18 cm³
生:我观察发现,这个位置多一个小正方体,这个位置少一个小正方体,我就想把多的这个小正方体补到这个位置,就摆成了一个长方体,长方体的长是 3 厘米,宽是 2 厘米,高是 3 厘米,长方体体积 = 长 × 宽 × 高,所以列式 3×2×3=18cm³。
师:同学们,你们都像他这样搭一搭。你们都算对了吗?像前 3 题,我们先观察是什么图形,并找到数据,再应用体积公式进行计算。而最后这道题,我们实际是用 “割补” 的方法,把一个不规则的图形转化成一个规则的图形,再应用体积公式进行计算。我们也可以用 “数小正方体” 的方法数出这个不规则图形的体积。
- 师:(出示牙膏盒、土豆) 谁的体积大?你是怎么想的?
【预设】学生提出转化、数小正方体等方法。
师:可以把不规则土豆的体积转化成可以测量计算的规则图形的体积,感兴趣的同学课后完成。
【设计意图】通过练习,使学生能正确计算长方体和正方体的体积,发展学生解决实际问题的能力。首尾呼应,创设完整的问题情境,拓展不规则物体的体积,强化了转化的思想方法,为之后的学习做好铺垫。
四、全课总结
师:同学们,请你闭上眼睛回顾一下,这节课我们一起研究了哪些知识?我们是怎样探究长方体、正方体体积计算方法的?(出示本课思维导图)睁开眼睛看一看,你学会了吗?
师:最后,老师想送大家一句名言, (出示(齐读): 天下事有难易乎,为之,则难者亦易矣;不为,则易者亦难矣。) 无论学习还是做事,是没有难和易之分的,只要你去学,你去做,再困难的事也会变得很容易。知难而进,是我们最好的学习态度。
这节课我们就上到这里,同学们再见!
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |
《长方体的体积》教学设计(二稿)
【教学内容】北师大版五年级下册第四单元 P41 P42 练一练 1-3
【教材分析】长方体、正方体是最基本的立体图形,是研究其他立体图形的基础,长方体、正方体体积的计算,是学生形成体积概念、掌握体积的计量单位和计算各种几何形体体积的基础。教科书重视引导学生经历知识的探究过程。首先安排了长方体体积与长方形面积的类比,启发学生猜测长方体的体积可能与长、宽、高有关;接着安排操作活动,引导学生用小正方体摆 3 个不同的长方体,并记录相关数据。通过观察、分析数据,逐步归纳得出长方体体积的计算方法。最后是自主探索正方体体积计算公式。
【学情分析】学生在第一学段直观地认识了长方体、正方体,并已经学习了长方形、正方形等平面图形以及它们周长和面积的计算。在本册的第二单元,学生学习了长方体、正方体的特征及表面积。在第四单元,学生学习了体积和容积、体积单位。
【学习目标】
1.结合具体情境和实践活动,探索并掌握长方体、正方体体积的计算方法;能正确计算长方体和正方体的体积;
2.培养学生动手操作、抽象概括、归纳推理的能力;发展空间观念;
3.激发学生学习数学、探究数学的兴趣;学会与人合作;学会倾听与质疑,养成独立思考的习惯。
【教学重点】
理解长方体体积公式的的推导过程,掌握长方体、正方体体积的计算方法。
【教学难点】
理解长方体的体积公式的推导过程。
【学习过程】
一、创设情境,体会体积计算方法的重要性
师:(PPT 出示一个长方体和一个正方体) 一个长方体和一个正方体正在为 “谁的体积大” 而争吵,你们能帮忙评判一下吗?
【预设】生:这怎么比较呀?得先求出它们的体积。
生:我想到了,把长方体和正方体分割成体积为 1 立方厘米的小正方体,分别数出小正方体的个数,就能比较它们的体积啦
生:你这个想法挺好,就是操作起来太麻烦了!而且在实际生活中,很多情况下,往往是不能用切割的方法来求长方体和正方体的体积的。
生:那怎么办?要是求长方体、正方体的体积,也能像求它们的表面积一样有计算方法就好了!
师:同学,我们一起来研究一下吧!
【设计意图】创设情境,激发学生学习数学、探究数学的兴趣。
二、探索长方体、正方体体积的计算方法
师:你能猜猜长方体的体积可能与什么有关吗?【问题一:长方体的体积可能与什么有关?】
【预设】生:长方形的面积与长和宽有关,我猜长方体的体积可能与长、宽和高有关。
生:我想结合图形来说说。长方体的宽和高不变,长减小一些,体积就变小了;长增大一些,体积就变大了。说明,体积和长有关。
生:长方体的长和高不变,宽增加,体积也随着增加;如果宽减少,体积也随着减少。说明,体积和宽有关。
生:长方体的长和宽不变,高增加,体积也随着增加;如果高减少,体积也随着减少。说明,体积和高有关。
生:长方体的长、宽、高越大,长方体的体积就越大;长方体的长、宽、高越小,长方体的体积就越小。
生:我们猜对了,长方体的体积果然与长、宽、高都有关系。
师:你们分析得没错,长方体的体积确实与长、宽、高都有关系。那到底有怎样的关系呢?【问题二:长方体的体积与长、宽、高有什么关系?】
【预设】生:长方形面积 = 长 × 宽,所以我猜,长方体的体积 = 长 × 宽 × 高
生:我通过预习,知道长方体的体积就是等于长 × 宽 × 高
师:让我们借助长方形面积公式的推导经验,用一些棱长为 1 厘米的小正方体摆出 3 个不同的长方体,记录它们的长、宽、高,完成下表,验证你的猜想。同学们,开始吧
【预设】生:我每排摆 3 个,摆 2 排,摆 2 层。我摆的这个长方体的长是 3 厘米,宽是 2 厘米,高是 2 厘米,共用了 12 个小正方体,长方体体积是 12 立方厘米。
生:我每排摆 5 个,摆 1 排,摆 3 层。我摆的这个长方体的长是 5 厘米,宽是 1 厘米,高是 3 厘米,共用了 15 个小正方体,长方体体积是 15 立方厘米。
生:我每排摆 4 个,摆 3 排,摆 2 层。我摆的这个长方体的长是 4 厘米,宽是 3 厘米,高是 2 厘米,共用了 24 个小正方体,长方体体积是 24 立方厘米。
生:这是我们整理的表格!棱长为 1 厘米的小正方体,体积是 1 立方厘米。摆这个长方体用了多少个小正方体,长方体的体积就是多少立方厘米。也就是说,长方体的体积等于体积单位小正方体的个数。这两列数据是相等的。
生:你们看,每排的个数 × 每层的排数,等于每层小正方体的个数,再 × 层数,正好等于小正方体的个数。
生:咦?大家看我们摆的长方体,我发现,每排小正方体的个数,就是长方体的长。每层的排数,就是长方体的宽。层数,就是长方体的高。那不就相当于长 × 宽 × 高就等于小正方体的个数了嘛!
生:长 × 宽 × 高等于小正方体的个数,也就等于长方体的体积喽!所以长方体的体积真的等于 长 × 宽 × 高!
师:通过操作,我们发现长方体的体积等于体积单位小正方体的个数;小正方体的个数 = 每排的个数 × 每层的排数 × 层数;每排小正方体的个数,就是长方体的长;每层的排数,就是长方体的宽;层数,就是长方体的高;长方体的体积等于 长 × 宽 × 高(出示)。长方体体积公式可以用字母来表示。体积用 V 表示,长用 a 表示,宽用 b 表示,高用 h 表示, V=a×b×h=abh(在这里,乘号可以省略不写)。
师:同学们,请你大声说说,我们是如何得到长方体体积公式的?
【设计意图】 结合实践活动,让学生探索长方体体积的计算方法;培养学生动手操作、抽象概括、归纳推理的能力,进一步发展空间观念;学会与人合作,学会倾听与质疑。
师:长方体的体积我们会计算了,那么如何计算正方体的体积?你有什么想法?【问题三】
【预设】生:我是这样想的,因为正方体是特殊的长方体,长方体的体积 = 长 × 宽 × 高,所以正方体的体积也等于 长 × 宽 × 高,正方体的长、宽、高都相等,也就是正方体的棱长。所以正方体的体积 = 棱长 × 棱长 × 棱长。(对比出示)
生:我是通过用小正方体摆大正方体的方法,来得出正方体体积的计算公式的。我每排摆 2 个,摆 2 排,摆 2 层。我摆的这个大正方体的棱长是 2 厘米,共用了 8 个小正方体,大正方体体积是 8 立方厘米。我每排摆 3 个,摆 3 排,摆 3 层。我摆的这个大正方体的棱长是 3 厘米,共用了 27 个小正方体,大正方体体积是 27 立方厘米。通过观察,我发现正方体的体积 = 棱长 × 棱长 × 棱长。
师:正方体体积公式也可以用字母来表示。
【预设】生:我知道,体积用 V 表示,棱长用 a 表示,正方体的体积公式用字母表示是 V=a×a×a = a3
师:这里 a3 读作 a 的立方或 a 的三次方,表示 3 个 a 相乘。
师:同学们,请你大声说说,我们是如何得到正方体体积公式的?
【设计意图】 鼓励学生借助正方体与长方体的关系,通过推理得出正方体的体积公式。
三、掌握计算方法,解决简单的实际问题
- 师:同学们,现在你知道它们谁的体积大了吗?
【预设】生:我想用今天学到的计算方法,但是不知道长、宽、高和棱长是多少,就不能计算呀
师:是的,要求长方体的体积必须知道长、宽、高。要求正方体的体积必须知道棱长。(再次出示有数据的) 同学们,请你算一算,比比它们谁的体积大?
生:3×3×3=27cm 2×2×7=28cm3 28cm3>27cm3 答:长方体的体积大。
【小结】师:你们真了不起,通过猜想、实验、验证总结出了长方体的体积计算公式。老师希望你们今后都能用这种方法来学习数学。
同学们,这些知识你们掌握了吗?我们一起来巩固练习一下。
- 课件出示 P42 - 练一练 2
师:我说你做(摆),用体积是 1 立方厘米的小正方体摆长方体。
【预设】生:我先来出题,1 排 5 个,2 排,2 层(PPT 出示数据提示),请你搭出这个长方体,并说出体积是多少?
生:我每排摆 5 个,摆 2 排,摆 2 层。我摆的这个长方体的长是 5 厘米,宽是 2 厘米,高是 2 厘米,5×2×2=20cm3,长方体体积是 20 立方厘米。
生:我再来出题,我这个长方体的体积是 12 立方厘米(PPT 提示),你能搭出这个长方体吗?
生:我共摆出 4 种。我每排摆 3 个,摆 4 排,摆 1 层。我摆的这个长方体的长是 3 厘米,宽是 4 厘米,高是 1 厘米,3×4×1=12cm3。 每排摆 2 个,摆 2 排,摆 3 层。我摆的这个长方体的长是 2 厘米,宽是 2 厘米,高是 3 厘米,2×2×3=12cm3。 每排摆 2 个,摆 1 排,摆 6 层。我摆的这个长方体的长是 2 厘米,宽是 1 厘米,高是 6 厘米,2×1×6=12cm3。 每排摆 12 个,摆 1 排,摆 1 层。我摆的这个长方体的长是 12 厘米,宽是 1 厘米,高是 1 厘米,12×1×1=12cm3,它们的体积都是 12 立方厘米。
师:大家看,体积相等的图形,摆法不同,形状也是不同的。
- 课件出示 P42 - 练一练 3
师:用体积是 1 立方厘米的小正方体摆成如下的图形,它们的体积各是多少?
【预设】生:我先观察,这个长方体的长是 3 厘米,宽是 2 厘米,高是 2 厘米,长方体体积 = 长 × 宽 × 高,所以列式 3×2×2=12cm3。
生:这个长方体的长是 5 厘米,宽是 3 厘米,高是 3 厘米,长方体体积 = 长 × 宽 × 高,所以列式 5×3×3=45cm3。
生:我先观察,这是正方体,它的棱长是 2 厘米,正方体体积 = 棱长 × 棱长 × 棱长,所以列式 2×2×2=8cm3。
生:最后这道题,怎样算呢?
生:我是用 “数一数” 的方法,我数了一下,一共有 18 个小正方体,所以体积是 18 cm3
生:我观察发现,这个位置多一个小正方体,这个位置少一个小正方体,我就想把多的这个小正方体补到这个位置,就摆成了一个长方体,长方体的长是 3 厘米,宽是 2 厘米,高是 3 厘米,长方体体积 = 长 × 宽 × 高,所以列式 3×2×3=18cm3。
师:同学们,你们都算对了吗?像前 3 题,我们先观察是什么图形,并找到数据,再应用体积公式进行计算。 而最后这道题,我们实际是用 “割补” 的方法,把一个不规则的图形转化成一个规则的图形,再应用体积公式进行计算。我们也可以用 “数小正方体” 的方法数出这个不规则图形的体积。
四、全课总结
师:同学们,请你闭上眼睛回顾一下,这节课我们一起研究了哪些知识?我们是怎样探究长方体、正方体体积计算方法的?(出示本课思维导图)睁开眼睛看一看,你学会了吗?
师:最后,老师想送大家一句名言, (出示:天下事有难易乎,为之,则难者亦易矣;不为,则易者亦难矣。) 无论学习还是做事,是没有难和易之分的,只要你去学,你去做,再困难的事也会变得很容易。知难而进,是我们最好的学习态度。这节课我们就上到这里,同学们再见!
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |
《长方体的体积》教学设计(一稿)
【教学内容】北师大版五年级下册第四单元 P41 P42 练一练 1-3
【学习目标】
1.掌握长方体和正方体体积公式的推导过程,理解长方体和正方体体积的计算公式;初步学会计算长方体和正方体的体积;
2.培养学生实际操作能力,同时发展他们的空间观念;培养学生动手操作、抽象概括、归纳推理的能力;
3.激发学生学习数学、探究数学的兴趣;学会与人合作,形成一定的评价与反思的能力;学会倾听与质疑,养成独立思考的好习惯。
【教学重点】:理解长方体体积公式的的推导过程,掌握长方体体积的计算方法。
【教学难点】:理解长方体的体积公式的推导过程。
【教学过程】
同学们,你们好!今天这节课我们一起来学习长方体的体积。首先,让我们一起来看看本节课的学习目标。
1.(在这节课中,我们要)结合具体情境和实践活动,探索并掌握长方体、正方体体积的计算方法,能正确计算长方体、正方体的体积,解决一些简单的实际问题。
2. 在观察、操作、探索的过程中,提高动手操作能力,进一步发展空间观念。
一、创设情景,体会体积计算方法的重要性
师:(PPT 出示一个长方体和一个正方体) 一个长方体和一个正方体正在为 “谁的体积大” 而争吵,你们能帮忙评判一下吗?
师:同学,我们一起来研究一下吧!
二、探索长方体、正方体体积的计算方法
师:你能猜猜长方体的体积可能与什么有关吗?【问题一:长方体的体积可能与什么有关?】
师:你们分析得没错,长方体的体积确实与长、宽、高都有关系。那到底有怎样的关系呢?【问题二:长方体的体积与长、宽、高有什么关系?】
生 1:长方形面积 = 长 × 宽,所以我猜,长方体的体积 = 长 × 宽 × 高
生 2:我通过预习,知道长方体的体积就是等于长 × 宽 × 高
师:让我们借助长方形面积公式的推导经验,用一些棱长为 1 厘米的小正方体摆出 3 个不同的长方体,记录它们的长、宽、高,完成下表,验证你的猜想。同学们,开始吧
生 1: 我每排摆 3 个,摆 2 排,摆 2 层。我摆的这个长方体的长是 3 厘米,宽是 2 厘米,高是 2 厘米,共用了 12 个小正方体,长方体体积是 12 立方厘米。(出示 PPT,填表和长宽高对应)
生 2: 我每排摆 5 个,摆 1 排,摆 3 层。我摆的这个长方体的长是 5 厘米,宽是 1 厘米,高是 3 厘米,共用了 15 个小正方体,长方体体积是 15 立方厘米。(出示 PPT,填表和长宽高对应)
生 3: 我每排摆 4 个,摆 3 排,摆 2 层。我摆的这个长方体的长是 4 厘米,宽是 3 厘米,高是 2 厘米,共用了 24 个小正方体,长方体体积是 24 立方厘米。(出示 PPT,填表和长宽高对应)
生 2:这是我们整理的表格!棱长为 1 厘米的小正方体,体积是 1 立方厘米。摆这个长方体用了多少个小正方体,长方体的体积就是多少立方厘米。也就是说,长方体的体积等于体积单位小正方体的个数。这两列数据是相等的。
生 1:你们看,每排的个数 × 每层的排数,等于每层小正方体的个数,再 × 层数,正好等于小正方体的个数。
生 2:咦?大家看我们摆的长方体,我发现,每排小正方体的个数,就是长方体的长。每层的排数,就是长方体的宽。层数,就是长方体的高。那不就相当于长 × 宽 × 高就等于小正方体的个数了嘛!
生 1:长 × 宽 × 高等于小正方体的个数,也就等于长方体的体积喽!所以长方体的体积真的等于 长 × 宽 × 高!
师:通过操作,我们发现长方体的体积等于体积单位小正方体的个数;小正方体的个数 = 每排的个数 × 每层的排数 × 层数;每排小正方体的个数,就是长方体的长;每层的排数,就是长方体的宽;层数,就是长方体的高;长方体的体积等于 长 × 宽 × 高(出示)。长方体体积公式可以用字母来表示。体积用 V 表示,长用 a 表示,宽用 b 表示,高用 h 表示, V=a×b×h=abh(在这里,乘号可以省略不写)。
师:同学们,请你大声说说,我们是如何得到长方体体积公式的?
师:长方体的体积我们会计算了,那么如何计算正方体的体积?你有什么想法?【问题三】
师:正方体体积公式也可以用字母来表示。
生 3:我知道,体积用 V 表示,棱长用 a 表示,正方体的体积公式用字母表示是 V=a×a×a = a3
师:这里 a3 读作 a 的立方或 a 的三次方,表示 3 个 a 相乘。同学们,请你大声说说,我们是如何得到正方体体积公式的?
三、掌握方法,解决简单的实际问题
师:同学们,现在你知道它们谁的体积大了吗?
师:是的,要求长方体的体积必须知道长、宽、高。要求正方体的体积必须知道棱长。(再次出示有数据的) 同学们,请你算一算,比比它们谁的体积大?
【小结】师:你们真了不起,通过猜想、实验、验证总结出了长方体的体积计算公式。老师希望你们今后都能用这种方法来学习数学。同学们,这些知识你们掌握了吗?我们一起来巩固练习一下。
课件出示练一练 2
师:我说你做(摆),用体积是 1 立方厘米的小正方体摆长方体。
师:大家看,体积相等的图形,摆法不同,形状也是不同的。
课件出示练一练 3
师:用体积是 1 立方厘米的小正方体摆成如下的图形,它们的体积各是多少?
师:同学们,你们都算对了吗?像前 3 题,我们先观察是什么图形,并找到数据,再应用体积公式进行计算。 而最后这道题,我们实际是用 “割补” 的方法,把一个不规则的图形转化成一个规则的图形,再应用体积公式进行计算。我们也可以用 “数小正方体” 的方法数出这个不规则图形的体积。
四、全课总结,布置作业
同学们,请你闭上眼睛回顾一下,这节课我们一起研究了哪些知识?我们是怎样探究长方体体积计算方法的?(出示本课思维导图)睁开眼睛看一看,你学会了吗?
最后,老师想送大家一句名言, (出示:天下事有难易乎,为之,则难者亦易矣;不为,则易者亦难矣。) 无论学习还是做事,是没有难和易之分的,只要你去学,你去做,再困难的事也会变得很容易。知难而进,是我们最好的学习态度。这节课我们就上到这里,同学们再见!
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |
团队在教学设计初期,大量查阅 “量感” 文献资料进行学习,并结合教学实践,形成了以下理论基础:“量感” 顾名思义就是对量的感受,详细地说,就是对事物时间、速度、尺寸、重量等的感官认识。教师应带领学生主动构建对物体量的意义感受,进而在数学教学里贯穿 “量感” 教学,通过实际体验增强学生对量的感受,从而形成良好的 “量感”。
一、联系生活实际,强化量感感知
数学与生活联系紧密。通过与生活结合展开教学体验,有助于学生增强感受,以推动学生建立量感。教师在教学量的相关知识时,应鼓励学生结合个人生活经验进行对比学习,进而强化他们估测事物的能力。
二、引导数学反思,推进量感提升
量感其实是学生内心的感觉,它的形成需要学生借助实践操作和思维反思。以往对量感的关注,大多是从实践、感受的角度去重视,但却没有意识到学生的反思活动也有助于量感的形成。事实上,仅有体验和感知是不够的,还需在感性经验的基础上,结合思维反思活动,将其提炼为内心的评价标准,进而形成有效的量感。也只有通过反思活动,才能将已有量感进行拓展,进而强化学生对量的感受,实现更准确的量感。
三、促进知识勾连,促进量感内化
量感由于是一种感觉,所以不是一朝一夕就能培养形成的,需要教师在学生的学习和生活中进行渗透,以丰富学生形成量感的途径。为此,需要教师把握量与其他数学知识的相关性,进而在相互贯穿中推动学生把量感内化于心,自觉地发挥量感在学习与生活中的作用。
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |
【教学内容】北师大版五年级下册第四单元 P41 P42 练一练 1-3
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |
【学习目标】 1.掌握长方体和正方体体积公式的推导过程,理解长方体和正方体体积的计算公式;初步学会计算长方体和正方体的体积; 2.过程与方法目标:培养学生实际操作能力,同时发展他们的空间观念;培养学生动手操作、抽象概括、归纳推理的能力; 3.情感态度与价值观目标:激发学生学习数学、探究数学的兴趣;学会与人合作,形成一定的评价与反思的能力;学会倾听与质疑,养成独立思考的好习惯。
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |
5年前 回复了 李德毅 创建的主题› 展示大赛-2021 › 【2021 春】辽宁大连基地李德毅五下《长方体的体积》 |