sxychcyj123

活动综述：首先感谢咱们新世纪小学数学给老师们搭建的这个平台，让老师们通过相互的交流，思维上的碰撞，产生智慧的火花，老师们在教学上有了很大的进步；其次感谢我的团队，从 2 月下旬到 4 月底，为期两个多月的时间，我的团队在一起研读课标，解读教材，制定教学目标、教学重难点，教学过程。我们团队每磨一次课，都在一起教研，哪个环节不合理就修改，总共经历 9 次的试讲，教学设计一共进行 4 次修改，这些艰辛的历程永远都有我的团队做坚强的后盾。在答辩环节，我们集思广益，想如何追问对方辩友，以及如何回答那两个固定问题，我们每个人在不影响正常教学的情况下，都尽自己最大的努力为此次活动献计献策；最后我想说，不论最终结果是什么，我们努力了就不悔，我们参与了就是进步。宝剑锋从磨砺出，梅花香自苦寒来，期待下次的参与！

《圆柱的体积》教学设计终稿

山西省运城市海仓学校 袁菁

教材分析：

本节课是北师大版六年级下册第一单元第三节的内容。纵观小学数学全套教材的 “图形与几何” 部分，可以清楚的看出图形的学习是循序渐进地。由立体图形的直观感知到立体图形结构、量化地刻画，是思维的进阶。通过长度、面积、角的一系列学习活动，让学生在类比、转化的思想中逐步形成一定层次的量感知觉。对于本册教材中所涉及的《圆柱与圆锥》这一章，先从面的旋转、圆柱的表面积、圆柱的体积、圆锥的体积，层次逐渐加深。通过圆柱的学习过程可以迁移学习圆锥。那么从本节课的角度我深入进行了教材分析：首先在情境引入中让学生直观的感知圆柱体积量的大小，体会圆柱体积的必要性和意义，定性分析圆柱的体积与什么有关系；在类比猜想中搭建圆柱等直柱体体积的知识结构，在实践操作中逐步探究，定量分析圆柱的体积计算方法；最后在练习应用中延展总结进一步发展学生的量感。

学情分析：

学生在五年级已经掌握什么是物体的体积，以及长方体、正方体的体积公式，学生对体积单位有一定的了解，并且对生活中常见实物的体积有一定的量感；在六年级上册中掌握了圆面积公式的推导。学习圆柱的体积之前，教材编排，先研究了圆柱的特征，知道圆柱各部分名称。对研究对象圆柱的 “形” 有了一定的了解。

前测情况：

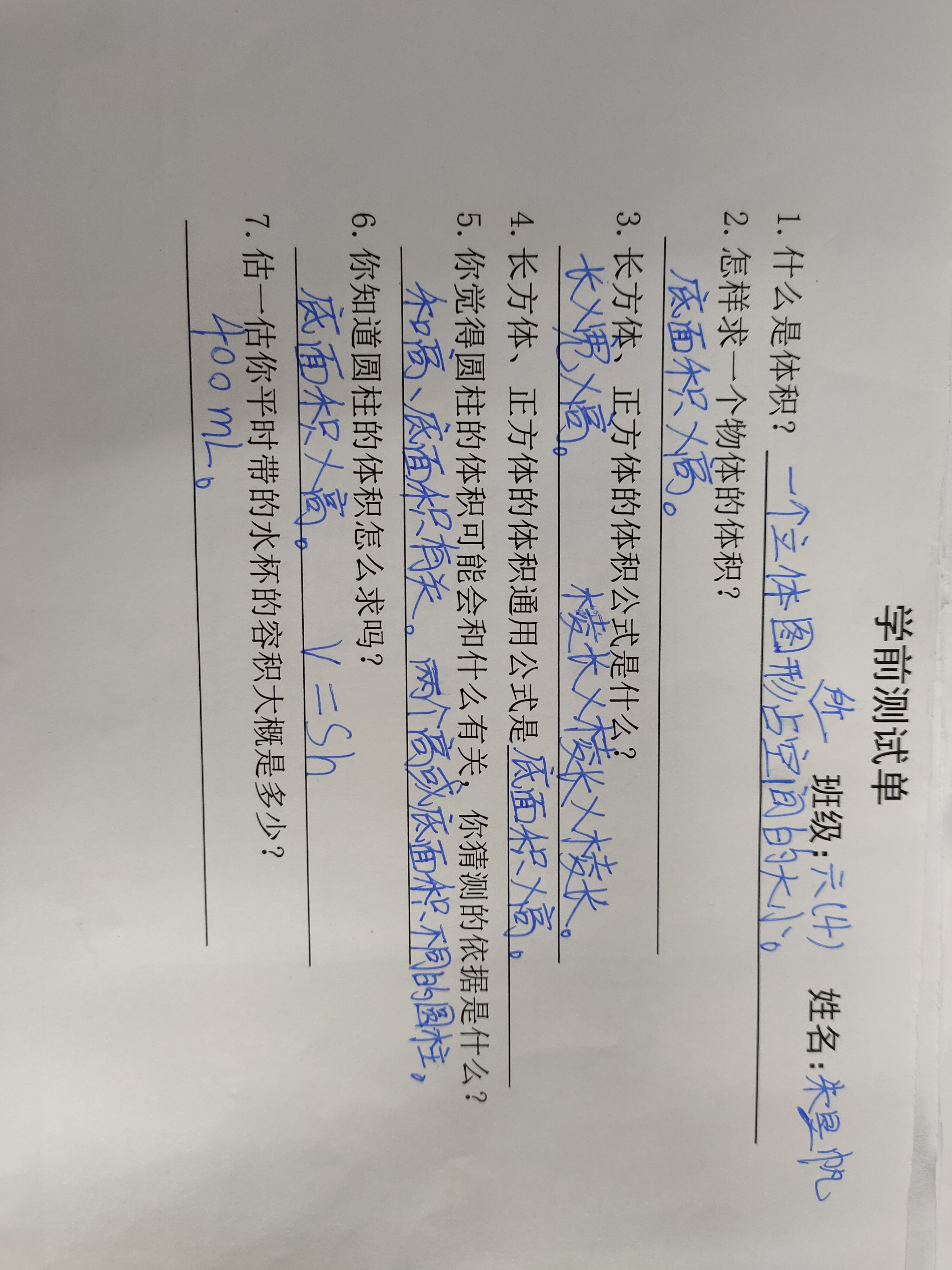
 对运城市海仓学校六（4）班学生做前测，在前测中发现 8%学生不能准确描述出体积的概念，66%的学生用公式计算一个物体的体积，34%的学生用转化法来解决一个物体体积的计算；96%的学生能正确表述出长方体、正方体的体积计算公式；88%学生会用底面积高来表示长方体、正方体的体积；76%的学生觉得圆柱的体积会与它的底面积和高有关；24%的学生知道圆柱的体积怎么计算；通过学生对水杯容积的估量，测出有 82%的学生有合理的量感。

基于这样的前测数据，紧紧依托学生的已有认知经验，顺势而导，以学定教，我将本节课的教学目标和教学过程进行如下设计。

教学目标:

1. 通过具体情境观察，实物感知等活动，直观感受物体体积的大小，发展量感和空间观念。

2. 通过圆柱与长方体的 “类比”，感悟数学知识的内在联系，经历 “猜想、验证” 探索圆柱体积计算方法的过程，体会 “类比”、“等积变形”、“极限思想” 等数学思想方法，引导学生将未知转化为已知知识来解决，培养学生 “学会学习” 的能力。

3. 掌握圆柱体积计算方法，能正确计算圆柱的体积，增强应用意识，进一步提升学生的量感。

教学重点：掌握和运用圆柱体积的计算公式。

教学难点：圆柱体积公式的推导过程。

教具准备：课件、圆柱小棒、圆柱积木、水杯、矿泉水、微课 3.0

学具准备：圆柱学具，学习清单

教学过程：

一、情境导入，唤醒量感意识

1. 对比中，体现量感

①让学生对比一根小棒和一个圆柱形积木，初步让学生感知两个圆柱体物体的大小。

②将小棒、圆柱形积木和故宫柱子的照片做进一步对比，体会故宫柱子的粗大。

（设计意图：从学生熟悉的小棒、积木引入，三种物体鲜明对比下，能更清晰让学生感知到故宫柱子的粗大，让学生对知识的探索产生欲望。“生活化感知” 为学生量感的形成奠定了坚实基础，初步唤醒学生的量感意识）

2. 追问中，引出课题

①这么粗的柱子需要多少木材？

②一个水杯能容纳多少毫升的水

明确研究主题求：圆柱的体积。

（设计意图：层层追问，借助学生对物体已有的量感意识，让学生体会圆柱体积或容积的实际含义，感受学习求圆柱体积计算方法的必要性，并提出怎样计算圆柱的体积。揭示本节课的课题《圆柱的体积》）

二、探索发现，建立体积模型

1. 回顾旧知，大胆猜测

①出示三个圆柱体（1 号 2 号等底不等高，2 号 3 号等高不等底），体会圆柱体积和底面积、高有关。

②回顾学过的立体图形体积公式，猜测圆柱体积的计算方法，并说明猜测依据。

预设 1：根据之前学过长方体、正方体立体图形的体积公式，长方体体积 = 长 × 宽 × 高，正方体 = 棱长 × 棱长 × 棱长，长方体和正方体的体积还可以用一个公式表示：底面积 × 高。

预设 2：长方体、正方体和圆柱都属于直柱体（上下底面相等，中间粗细均匀）。

（设计意图：本环节让学生经历怎样求圆柱体积的计算方法的猜想过程，体会类比、转化等数学思想方法。因为长方体与正方体的体积都是 “底面积 × 高”，长方体、正方体是直柱体，而圆柱也是直柱体，因此通过类比可以产生猜想：圆柱的体积计算方法也可能是 “底面积 × 高”。）

2. 动手操作，验证猜测

猜测不等于事实。我们用什么方法来验证它是否正确呢？ 请同学们说说自己的想法。（小组同学相互交流自己的想法）

（1）直观感知

预设：摞硬币，拿一些一元硬币，当我们往上摞到一定高度时，这个圆柱的体积不断变大，这样我们会很直观的感知圆柱的体积是底面积乘高。

（2）等积变形

预设：学生借助《圆面积》推导思路，将圆等分成若干份，拼成近似的长方形，这里将一个曲面图形转化为长方形，借助这个思想，我们可以把圆柱形等分成若干等份，拼成近似的长方体。

（设计意图：激发学生思维，让学生知道数学新知识的学习都是建立在旧知识的基础上，培养学生的转化思想、化曲为直和极限的思想，借助这些数学素养为解决新知打下坚实的基础，同时知识间的建构显得非常重要。）

3. 小组汇报，得出结论

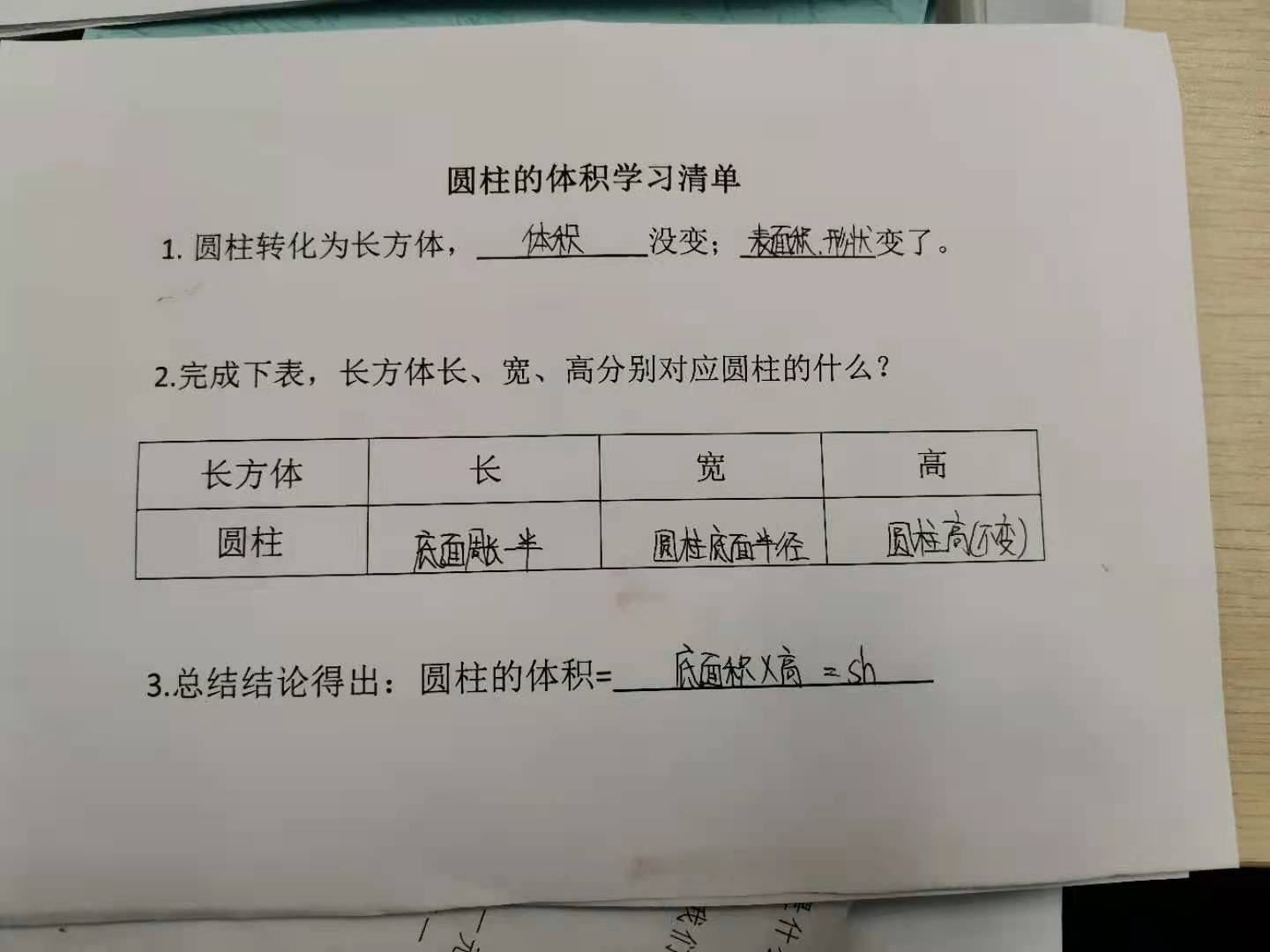
以小组为单位，依据学习清单进行汇报。

预设：将圆柱体等分成若干份，将其拼成近似的长方体，在这个转化过程中，物体的体积没有发生变化，形状变了，还有表面积也变了，而且是变大了（增加了两个面）。

长方体的长相当于圆柱底面圆周长的一半，宽相当于底面圆半径，高相当于圆柱的高。 观看新世纪微课 3.0 视频，把圆柱等分的份数越多，越接近长方体，更清楚明白它们之间的关系。 通过观察与思考：长方体体积 = 长 × 宽 × 高，长对应 ，宽对应，高对应，得出圆柱体积公式：，而就是圆柱底面圆面积，所以圆柱的体积 = 底面积 × 高。

（设计意图：让学生亲身经历知识的形成过程，使学生在操作、观察、对比、讨论、交流中，推导出圆柱体积公式，从中让学生正真体会到 “等积变形” 数学思想。苏霍姆林斯基曾说，让学生体验到自己在亲身参与掌握知识的情感，乃是唤起少年特有的对知识的兴趣的重要条件。在实践中体验 “量”，在体验中获得对 “量” 的独特感受。初步建立模型：圆柱体积）

三、理解应用，进一步发展量感 1. 计算立体图形的体积。

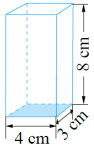
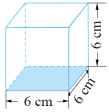
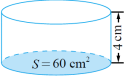
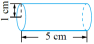
2. 解决情境问题 ------ 故宫柱子体积

底面半径 0.4m，高 5m，这根柱子需要多少木材？ 教师引导学生，让学生感知柱子的粗和高。

（设计意图：学以致用，感受故宫柱子体积，学生亲身感受，培养学生量感，发展空间观念。）

3. 出示一个杯子，和一瓶矿泉水，这个杯子能装下这瓶水吗？

预设：能或者不能，引出准确计算的必要性。

教师给出杯子里面底面直径 6cm，高 10cm 和矿泉水瓶的容积。

（设计意图：此题进一步加深学生对圆柱体积公式的理解，知道圆柱的体积不仅指物体所占空间的大小，还可以指物体所容纳的多少。在前面学生建立量感的基础上，进行应用，让学生的量感进步提升。）

四、总结归纳，搭建知识体系 通过本节课的学习大家有什么收获？

华罗庚教授曾把读书的过程归纳为 “由薄到厚” 两个阶段，这应该是科学研究、实践研究都要经历的过程，在这个过程中，认识也会伴随研究与实践的深入由博返约。其实这次活动我就深有感受，从刚开始我们团队想各种各样的导入、教具等，到最后很简练从学生熟悉的小棒、积木对比出故宫柱子的粗、大，量感无形渗透，很巧妙很简练的将本节课讲授完成，学生课堂表现很出彩。

3 稿的设计将培养学生量感体现的淋淋尽职，而且还培养学生学会学习的数学素养。就是这样在不断打磨中不断进步，学无止境，教学路上永远都在不断阅读，不断思考，不断进步。

三稿的设计，从学生熟悉的小棒、积木来对比故宫柱子的大，从导课就体现量感的培养，在二稿的基础上更高层次接近本次活动的主题，同时三稿在后面计算题的基础上也加入量感的渗透，最终通过本节课的学习，学生对 2 立方米的柱子有了更深的印象，而且也会借助这个基础量，估计出生活中一些圆柱体的体积大概有多少。所以此次设计更好的加深了量感在学生头脑中的印象。

2 稿上完以后，在 1 稿的基础上，课堂导入环节进行修改，同时课后的习题也有所变动。本次修改主要基于徐斌老师的无痕教育，所以本节课就一个杯子和一瓶矿泉水贯穿整堂课，由浅入深，无痕教育体现的淋淋尽职。但是通过团队的听课以及李主任的指导，问题是本节课设计的面有点窄，紧紧围绕着液体的圆柱展开教学，没有设计固体圆柱的求解和讲解，这样给学生们的知识面不够全面。

我们团队可以思考：可以加入生活的素材多点，真正的达到培养学生的量感，让量感真是发生。加油。。。。。。