18891560520

二稿反思：

设计二稿的教学依然重点体现了以下三个特点：

1. 重视学生的已有知识基础。学生之前已经学习过长方形、平行四边形、三角形等平面图形的面积，有了一定的探究图形面积的经验。因此在学习新知前，设计了一系列的回顾旧知的问题，目的唤醒学生已有的知识积淀，帮助学生总结到探究图形的面积，数格子和 “转化” 是较为普遍的方法，同时 “转化” 也是探究新识、解决数学问题最常用的方法，为下面推导圆面积公式做好了铺垫。

2. 重视学生的动手操作。由于圆是平面上的曲线图形，要将其转化为学过的直线图形，稍有难度。这时，借助直观的圆片，通过动手操作和体验让课堂富有了灵动的色彩。在引导学生思考：如何才能化曲为直后，孩子们以小组为单位开始了动手操作。课前的充分准备：圆形纸片、学习记录单、小刀、剪刀等，保证了课堂上动手操作的效果。为了探究出结果，孩子们小心翼翼地折、剪、拼、观察、对比、推导。

3. 重视数学思想方法的渗透。动手操作的过程中，有的小组将圆等分成 8 份，有的等分成 16 份…… 剪拼的过程中，孩子们亲身体验了 “化曲为直”，“化新知为旧知” 的转化的思想。

通过对不同等分拼成的近似的平行四边形，孩子们明白了：将圆平均分成的份数越多，拼成的图形就越接近平行四边形，无形中又渗透了极限的思想。

推导出圆面积的计算公式后，我带着孩子们回顾了整个的探究过程，总结出了探究圆面积的方法：动手操作 —— 观察比较 —— 梳理推导。为学生以后学习图形面积、体积的计算奠定了基础。

不足之处：

1. 导课部分改为旧知导入后，注重了对前期平面图形面积计算方法的阐述，导致导入部分用时太多，影响了整节课的时间分配。

2. 学生在动手操作时，出现了将圆转化为近似梯形的情况，由于时间紧张，推导过程较为复杂，学生直接放弃。此时，老师没有及时的指导，错过了精彩的生成。

3. 学生的探究过程还是较为费时，共用时 9 分钟。随后还要再想办法提高小组合作效率。

一稿反思：

一稿反思：

圆的面积（一）的教学重点是圆面积公式的推导过程，教学中，我努力发挥学生的主体作用，为学生留足充分的探究时间，让学生亲身经历圆面积公式的推导过程。因此本节课主要体现了以下几个特点：

1. 重视学生的已有知识基础。学生之前已经学习过长方形、平行四边形、三角形等平面图形的面积，有了一定的探究图形面积的经验。因此在学习新知前，设计了一系列的回顾旧知的问题，目的唤醒学生已有的知识积淀，帮助学生总结到探究图形的面积，数格子和 “转化” 是较为普遍的方法，同时 “转化” 也是探究新识、解决数学问题最常用的方法，为下面推导圆面积公式做好了铺垫。

2. 重视学生的动手操作。由于圆是平面上的曲线图形，要将其转化为学过的直线图形，稍有难度。这时，借助直观的圆片，通过动手操作和体验让课堂富有了灵动的色彩。在引导学生思考：如何才能化曲为直后，孩子们以小组为单位开始了动手操作。课前的充分准备：圆形纸片、学习记录单、小刀、剪刀等，保证了课堂上动手操作的效果。为了探究出结果，孩子们小心翼翼地折、剪、拼、观察、对比、推导。

3. 重视数学思想方法的渗透。动手操作的过程中，有的小组将圆等分成 8 份，有的等分成 16 份…… 剪拼的过程中，孩子们亲身体验了 “化曲为直”，“化新知为旧知” 的转化的思想。

通过对不同等分拼成的近似的平行四边形，孩子们明白了：将圆平均分成的份数越多，拼成的图形就越接近平行四边形，无形中又渗透了极限的思想。

推导出圆面积的计算公式后，我带着孩子们回顾了整个的探究过程，总结出了探究圆面积的方法：动手操作 —— 观察比较 —— 梳理推导。为学生以后学习图形面积、体积的计算奠定了基础。

不足之处：

1. 课堂中教师引的过多，有些限制学生的思维，课堂氛围不是很活跃。

2. 小组探究时，费时较多，导致课堂时间分配不均。

3. 练习二的设计，重在应用圆的面积，计算的成分多。没有达到本节课知识巩固的最佳效果。

教案终稿：

《圆的面积（一）》教学设计终稿

教学内容：

北师大版小学数学六年级上册 14、15 页《圆的面积（一）》

教材分析：

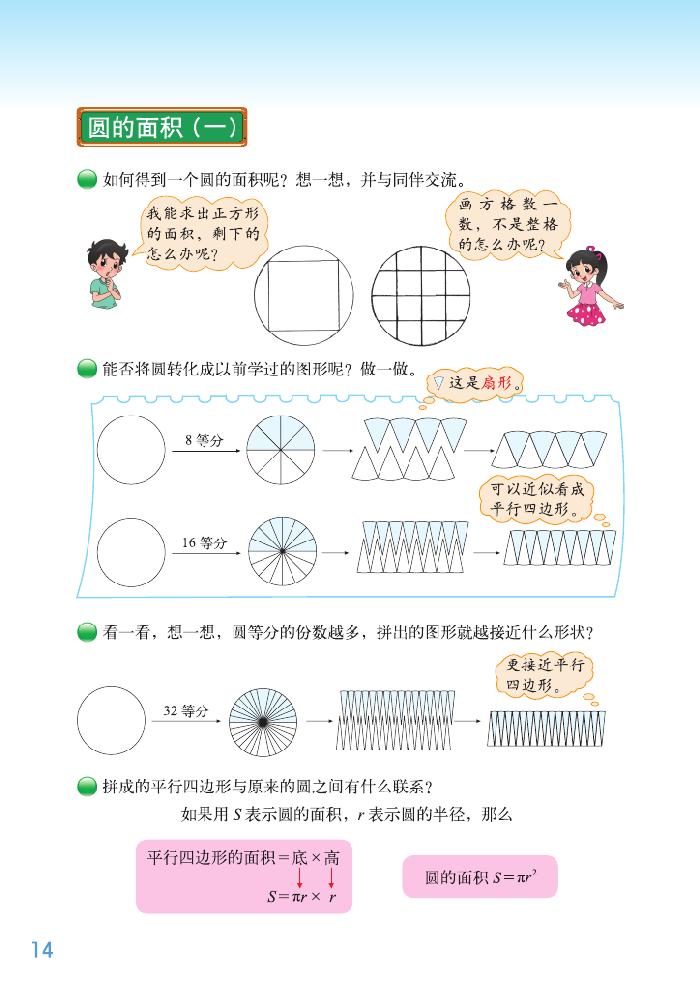
圆的面积是小学阶段学生学习几何知识的重要内容，是继学习了平行四边形、三角形、梯形面积后的延伸。考虑到学生的认知水平，教材先用方格纸为工具进行度量，以得到圆的面积的近似值；然后采用分割的方法将圆转化为近似的平行四边形，在无限细分的情况下进而得出圆面积的计算公式。

教学目标：

1. 主动建构并掌握圆面积的计算公式，并能运用公式解决简单的实际问题。

2. 经历动手折拼，观察比较、分析概括等数学活动，发展学生的合情推理能力，同时渗透 “转化”、“极限”、“化曲为直” 的数学思想，形成解决问题的基本策略。

3. 在寻求圆面积公式的数学活动中，体验数学问题的探索性和挑战性，激发学习数学的好奇心。

教学重点：

理解并掌握圆面积计算的推导过程，并能运用计算公式解决简单的实际问题。

教学难点：

如何将圆转化为已知图形进行面积公式的推导。

教具准备：

可等分的圆形教具，课件

教学过程：

一、复习旧知，导入新课

同学们，截止到目前为止，我们都学习过哪些平面图形的面积？（长方形、正方形、平行四边形、三角形、梯形）它们的面积都是怎么得到的？比如长方形面积

配合课件演示：

长方形的面积是通过摆方块，数格子得到的；

那平行四边形的面积呢？对也可以用数格子的方法。

之前还通过什么方法得到呢？是的我们通过剪、拼将平行四边形转化为学过的长方形，进而得到 S _{平行四边形} = 底  × 高；

同样，三角形的面积也可以转化为平行四边形进而得到 S _三角形 = 底  × 高 ÷ 2；

一句话总结一下，这些平面图形的面积，都可以怎样得到呢？

（数格子或转化的方法）

这节课我们继续探究平面图形的面积。想知道是什么图形吗？（圆）

师：圆的面积该如何得到呢？这节课我们一起来探究圆的面积（一）。

二、动手操作，探究新知。

（一）提出问题，独立思考：

1. 提问：你们想用什么方法得到一个圆的面积呢？（数格子、转化）

数格子，行不行，试试就知道。

2. 自主完成。

自己尝试数一数。

3. 同桌交流。（重点交流：数的过程以及结果。）

汇报时重点突出学生估的方法：如先数满格，再估四周，最后估出整圆的面积。

生：大约是 28 格。

师：这只是圆面积的近似值，能得到准确的圆面积吗？（不能）为什么？

4. 追问：怎样才能得到准确的圆的面积呢？

（二）动手操作，转化推导。

1. 问：那还可以用什么方法呢？（转化）想转化为什么图形？该如何转化呢？（剪、拼）

剪、拼、转化，任务量有点大，我们小组合作完成。

3. 小组合作完成：

请看合作要求：

A 动手做：剪一剪，拼一拼，尝试将手中的圆转化为学过的图形。

B 比一比：转化前后，图形的什么变了，什么没变？

C 说一说：转化前后，两个图形各部分之间有怎样的关系？

D 写一写：尝试写出圆面积的计算公式。

温馨提示：操作过程中注意用刀安全。

4. 聚集展示：

预设：

方法一： 转化为近似的平行四边形

S _{平行四边形} =     底     × 高

S _圆 =  圆周长的一半 × 半径

=  πr × r²

=  πr²

观察比较：请大家观察黑板上几组同学的学具，你发现了什么？

是的，将圆等分的份数越多，分成的扇形的弧度就越小，拼成的图形就起接近平行四边形。如果继续将圆等分下去会怎么样？ 一起看看。课件动态演示将圆 32 等份、64 等份、128 等份后拼成的图形。

小结：的确， 我们看到了如果一直将圆无限等分下去，分的份数越多，拼成的图形就越接近长方形。孩子们知道吗，这就是数学中非常重要的极限思想。今天大家可以记住这个词，在以后的数学学习中，你们肯定还会再遇到它。那时你对它的了解应该会更深刻。

（三）回顾梳理，总结方法：

千金难买回头看，同学们，一起来回顾一下我们刚才的探究过程，我们是怎么得到圆的面积计算方法的呢？

动手操作（将圆 转化 为平行四边形 / 长方形）

观察发现（圆与平行四边形 / 长方形各部分的关系）

梳理推导（S _圆 = πr²）

三、拓展延伸，巩固深化

同学们关于圆的面积，还有人进行了这样的研究，一起来看看。

巩固深化：

出示课本练一练第 2 题。

看一看，比一比，你发现了什么？

圆的面积比圆外的多边形面积小，比圆内多边形的面积大。

圆内接或圆外贴的多边形的边数越多，它的面积就越接近圆的面积。

追问：思考着这道题，你有没有想到一个词？对了，极限思想。观察发现上述规律的同时，又加深了我们对极限思想的理解。

四、布置作业，课后思索

在拼摆的过程中，有些同学把圆拼成了近似的三角形、梯形。你能根据这样的转化，验证我们这节课探究出的圆面积的计算方法吗？请同学们课后完成。

五、回顾整理，全课总结

同学们，这节课我们一起通过转化的方法，推导出了圆面积的计算方法，你能说说本节课，你有哪些收获吗？

教案二稿:

《圆的面积（一）》教学设计二稿

教学内容：

北师大版小学数学六年级上册 14、15 页《圆的面积（一）》

教材分析：

圆的面积是小学阶段学生学习几何知识的重要内容，是继学习了平行四边形、三角形、梯形面积后的延伸。考虑到学生的认知水平，教材先用方格纸为工具进行度量，以得到圆的面积的近似值；然后采用分割的方法将圆转化为近似的平行四边形，在无限细分的情况下进而得出圆面积的计算公式。

教学目标：

1. 主动建构并掌握圆面积的计算公式，并能运用公式解决简单的实际问题。

2. 经历动手折拼，观察比较、分析概括等数学活动，发展学生的合情推理能力，同时渗透 “转化”、“极限”、“化曲为直” 的数学思想，形成解决问题的基本策略。

3. 在寻求圆面积公式的数学活动中，体验数学问题的探索性和挑战性，激发学习数学的好奇心。

教学重点：

理解并掌握圆面积计算的推导过程，并能运用计算公式解决简单的实际问题。

教学难点：

如何将圆转化为已知图形进行面积公式的推导。

教具准备：

可等分的圆形教具，课件

教学过程：

一、复习旧知，导入新课

同学们之前我们都学习过哪些平面图形的面积？（长方形、正方形、平行四边形、三角形、梯形）它们的面积计算都是怎么得到的？我们一起回忆下。

配合课件演示：

长方形的面积是通过摆方块，数格子得到 S _长方形 = 长 × 宽；

平行四边形的面积也可以数格子，请看，方格中的这个平行四边形面积是多少呢？

对，同学们是先数满格，再将不是满格的拼成满格，最后数出平行四边形的面积。

那平行四边形的面积还可以怎样得到呢？

配合课件演示，是的我们是通过剪、拼将平行四边形转化为长方形，进而得到 S _{平行四边形} = 底  × 高；

那三角形的面积呢？

配合课件演示，是将两个完全相同的三角形拼在一起，转化为平行四边形得到 S _三角形 = 底  × 高 ÷ 2；

师：之前这些平面图形，我们都是通过（数格子或转化的方法）探究出来的。这节课我们继续探究平面图形的面积。想知道是什么图形吗？（圆）它跟之前认识的那些平面图形有什么区别？（曲线型图形）想不想挑战一下，来探究圆的面积？

师：这节课我们一起来探究圆的面积（一）。

二、动手操作，探究新知。

（一）提出问题，独立思考：

1. 提问：你们打算用什么方法得到一个圆的面积呢？（数格子、转化）

数格子，行不行，试试就知道。

2. 自主完成。

请看屏幕，尝试用 “数” 的方法得到图中圆的面积。

3. 指名交流。（重点交流：数的过程和结果。）

汇报时重点突出学生估的方法：如先数满格，再估四周，最后估出整圆的面积。

4. 追问：你觉得这种方法怎么样？（不能准确的得到圆的面积）

（二）动手操作，转化推导。

1. 问：那还可以用什么方法呢？（转化）

想转化为什么图形？（长方形、平行四边形……）

该如何转化呢？（剪、拼）

这个任务有点大，我们小组合作来完成。

3. 小组合作完成：

合作要求：

A 动手做：剪一剪，拼一拼，尝试将手中的圆转化为学过的图形。

B 比一比：转化前后，图形的什么变了，什么没变？

C 说一说：转化前后，两个图形各部分之间有怎样的关系？

D 写一写：尝试写出圆面积的计算公式。

4. 聚集展示：

预设：

方法一： 转化为近似的平行四边形

S _{平行四边形} =     底     × 高

S _圆 =  圆周长的一半 × 半径

=  πr × r²

=  πr²

观察比较：请大家观察黑板上几组同学的学具，你发现了什么？

是的，将圆等分的份数越多，分成的扇形的弧度就越小，拼成的图形就起接近平行四边形。如果继续将圆等分下去会怎么样？ 一起看看。课件动态演示将圆 32 等份、64 等份、128 等份后拼成的图形。

小结：的确， 我们看到了如果一直将圆无限等分下去，分的份数越多，拼成的图形就越接近长方形。孩子们知道吗，这就是数学中非常重要的极限思想。今天大家可以记住这个词，在以后的数学学习中，你们肯定还会再遇到它。那时你对它的了解应该会更深刻。

（三）回顾梳理，总结方法：

千金难买回头看，同学们，一起来回顾一下我们刚才的探究过程，我们是怎么得到圆的面积计算方法的呢？

动手操作（将圆 转化 为平行四边形 / 长方形）

观察发现（圆与平行四边形 / 长方形各部分的关系）

梳理推导（S _圆 = πr² ）

三、拓展延伸，巩固深化

同学们关于圆的面积，还有人进行了这样的研究，一起来看看。

1. 巩固深化：

出示课本练一练第 2 题。

看一看，比一比，你发现了什么？

圆的面积比圆外的多边形面积小，比圆内多边形的面积大。

圆内接或圆外贴的多边形的边数越多，它的面积就越接近圆的面积。

追问：思考着这道题，你有没有想到一个词？对了，极限思想。观察发现上述规律的同时，又加深了我们对极限思想的理解。

2. 拓展延伸：

可以将圆转化为平行四边形，那可不可以将它转化为长方形呢？

学生独立思考，指名学具演示汇报。

S _长方形 =      长     × 宽

S _圆 =  圆周长的一半 × 半径 =  πr × r² =  πr²

四、布置作业，课后思索

在拼摆的过程中，有同学把圆拼成了近似的三角形、梯形。你能根据这样的转化，验证圆面积的计算方法吗？请同学们课后完成。

五、 回顾整理，全课总结 同学们，这节课我们一起通过转化的方法，推导出了圆面积的计算方法，你能说说本节课，你有哪些收获吗？

https://v.youku.com/v_show/id_XNTgwNjU2MTk0MA==.html?spm=a2hcb.playlsit.page.1

教案一稿：

《圆的面积（一）》教学设计

教学内容：

北师大版小学数学六年级上册 14、15 页《圆的面积（一）》

教材分析：

圆的面积是小学阶段学生学习几何知识的重要内容，是继学习了平行四边形、三角形、梯形面积后的延伸。考虑到学生的认知水平，教材先用方格纸为工具进行度量，以得到圆的面积的近似值；然后采用分割的方法将圆转化为近似的平行四边形，在无限细分的情况下进而得出圆的面积计算公式。

教学目标：

1. 主动建构并掌握圆面积的计算公式，并能运用公式解决简单的实际问题。

2. 经历动手折拼，观察比较、分析概括等数学活动，发展学生的合情推理能力，同时渗透 “转化”、“极限”、“化曲为直” 的数学思想，形成解决问题的基本策略。

3. 在寻求圆面积公式的数学活动中，体验数学问题的探索性和挑战性，激发学习数学的好奇心。

教学重点：

理解并掌握圆面积计算的推导过程，并能运用计算公式解决简单的实际问题。

教学难点：

如何将圆转化为已知图形进行面积公式的推导。

教具准备：

可等分的圆形教具，课件

教学过程：

一、创设情境，导入新课

出示图片：

师：公园里我们经常会看到这种喷灌设备，如果这个喷水头旋转一周，会形成一个什么图形？（圆形）

师：如果要求它能喷灌的面积是多大实际上是求谁的面积？

生：圆

师：这节课我们就来研究圆的面积（一）。

二、动手操作，探究新知。

（一）提出问题，独立思考：

1. 问：同学们想一想，圆的面积大小会与圆的什么有关系呢？（半径、直径）

我们如何得到一个圆的面积呢？想一想，与同桌交流。

提示： 圆是一个平面图形。回想一下，我们之前是如何得到一个平面图形的面积的？如：平行四边形面积怎样得到的？

是的，我们是通过数方格的方法，以及将其转化为长方形推导出平行四边形面积计算公式的。

2. 问：那么圆的面积可不可以也用这样的方法呢？如：数方格

请同学们拿出 1 号学习单，尝试用 “数” 的方法得到图中圆的面积。

指名交流。（重点交流：数的过程和结果。）

出示课本图：

3. 追问：你觉得这种方法怎么样？（过程麻烦、求得的结果不够准确）

（二）动手操作，转化推导。

1 问：那可不可以将圆转化为我们学过的图形求出面积呢？可以转化为什么图形？想试试吗？

质疑：想一想，我们以前学习过哪些平面图形的面积？（长方形、正方形、平行四边形、三角形、梯形）这些图形都是直线型图形，而圆是一个曲线图形，怎么分割才能化曲为直呢？

对，有同学说可以沿直径对折，多次对折后就可以将圆等分为一个个什么图形呢？三角形？准确的说是近似的三角形。

2. 问：你能想办法将等分后的圆拼、摆成我们学过的图形吗？

3. 自主尝试：

动手折拼一拼，尝试将手中的圆片转化为已学过的图形。

4. 合作交流：

A 比一比：转化前后，图形的什么变了，什么没变？

B 说一说：转化前后，两个图形各部分之间有怎样的关系？

C 写一写：尝试写出圆面积的计算公式。

5. 聚集展示：

预设：

方法一： 转化为近似的平行四边形

S _{平行四边形} =     底     × 高

S _圆 =  圆周长的一半 × 半径

      =  πr × r²

 =  πr2

方法二： 转化为近似的长方形                  

S _长方形 =      长     × 宽

S _圆 =  圆周长的一半 × 半径 =  πr × r²  =  πr²

观察比较：老师收集了几组同学的学具，一起来看看，你发现了什么？

如果继续将圆等分下去会怎么样？ 课件演示将圆 32 等分

师生小结：是的， 如果继续将圆等分下去，等分的份数越多，拼成的图形就越接近平行四边形。

（三）回顾梳理，总结方法：

千金难买回头看，同学们，回忆一下我们刚才是怎样得到圆面积的计算公式的？

动手操作（将圆 转化 为平行四边形 / 长方形）

观察发现（圆与平行四边形 / 长方形各部分的关系）

梳理推导（S _圆 = πr² ）

三、联系生活，巩固深化

刚才同学们推导出了圆面积的计算公式，谁说一说计算圆的面积需要知道什么？（半径、直径）

1. 现在我们回过头来解决课伊始提出的问题。

如果这个喷水头喷水的半径为 3 米，喷头转动一周，能浇灌多大面积的农田？

独立计算，指名交流。

2. 下图中正方形的边长为 5 厘米，你能计算出整个图形的面积是多少平方厘米吗？

同桌讨论，尝试完成，指名汇报。

四、课后思索，拓展延伸

在前面拼摆的过程中，有些同学把圆拼成了近似的三角形、梯形。你能根据这样的转化，应用本节课学习的方法也试着推导出圆面积的计算方法吗？请同学们课后完成。

五、回顾整理，全课总结

同学们，这节课我们一起通过转化的方法，推导出了圆面积的计算方法，你能说说本节课，你有哪些收获吗？

选课思考：

量感是对量的感受，在小学阶段，量感主要是指对长度、面积等的感性认识。史宁中教授说：量感是指对物体的长度、面积和体积等的感觉，教师要通过主题活动的形式进行教学。更重要的是知道在什么情况下用什么计量单位度量。张丹老师也说过：量感强调的是对单位的感觉，它体现在实际生活中如何选择合适的方法进行度量；体会怎样估计面积、得到面积等，以及如何表达自己的思考过程。

六年级上册《圆的面积（一）》一课主要是让学生借用方格纸估计圆的面积大小，并学会选用合理的方法度量圆的面积，进行得到圆的面积计算公式。思考后，我们认为本课完全可以 “在度量活动中发展学生的量感”。

度量即测量，是指用一个带单位的数值来描述可测量的物体或现象的某一属性，从而形成具有特殊含义的 “量”。如圆的面积的度量。

度量的方法有：单位计量，如数格子，这是度量的基本治动；还有工具计量，如长度、质量、角度等都可以直接进行工具计量，这是度量的核心技能；还有公式计量，这是度量的常用方法。

本节课，我遵循学生的认知规律，采用两种度量方式，设计一个探究活动，为学生留够充分的时间和空间，以达到 “在度量中发展学生量感” 的目标。

最后，我们工作室成员将一起聚焦 “学会学习 —— 发展学生量感” 这一主题，借助《圆的面积（一）》这节课，深入探索发展学生量感的有效策略，为学生的终身发展奠基。

活动主题解读：

说起 “量感” 大家可能会觉得有些陌生，但说起 “量” 一定不陌生。常见的 “量” 有长度，面积，体积，时间，重量，角度等等。“量感” 归根到底是对量的一种 “感受”，是指视觉、触觉等感官对物体的规模、程度、速度等方面的感觉，也就是对物体的大小、多少、轻重、厚薄等的感性认识。然而在数学教学中，老师们大多注重相同量之间的换算，“量感” 常常被忽略。因为要培养学生真实有意义的 “量感”，需要老师们付出更多的时间或者专门设计一些活动来进行。

而本次活动的主题便是 “学会学习 —— 发展学生 “量感” 的学习方式探索”，这便为我们提供了一次专题研究的机会，要求教师重新审视自己的课堂教学模式，重新定位自己的教学目标的达成，以便设计出更能凸显学生主体地位的学习方式，能设计出有效发展学生 “量感” 的教学活动，从而帮助学生建立这种看不见、摸不着，却能终身受益的核心素养 ——“量感”。