圆锥的体积教学设计二稿

教学目标：

1、使学生探索并初步掌握圆锥体积的计算方法和推导过程；

2、使学生会应用公式计算圆锥的体积并解决一些实际问题；

3、提高学生实践操作、观察比较、抽象概括的能力，发展空间观念；

4、使学生在经历中获得成功的体验，体验数学与生活的联系。

教学重点：

使学生初步掌握圆锥体积的计算方法并解决一些实际问题。

教学难点：

探索圆锥体积的计算方法和推导过程。

教具准备：

1、多媒体课件。

2、等底等高、等底不等高、等高不等底的圆锥和圆柱，水、学习单等。

教学过程：

1、复习导入，温习旧知。 教师提问发长方体、正方体体、和原圆柱的同样体积公式，从而引出学习有关圆锥体积的相关知识内容。

2、动手实践，操作验证。

（1）小组有顺序地领取材料，填写材料单。 学生分组操作实验，教师巡回指导。

（其中 8 个小组的实验材料：等底等高的圆柱形和圆锥形容器各一个； 2 个小组的实验材料：等底不等高圆柱形和圆锥形容器各一个；另外 2 个小组的实验材料：等高不等低圆柱形和圆锥形容器各一个）

（2）小组合作实验，并填写实验报告单。

（3）汇报结果，实物投影展示实验报告单。

（4）组际交流，得出结论:

结论 1: 圆锥的体积 V 等于和它等底等高圆柱体积的三分之一。

结论 2: 等底不等高的圆锥体与圆柱体，圆锥的体积是圆柱体积的二分之一。

结论 3: 等高不等底的圆锥体与圆柱体，圆锥的体积是圆柱体积的四分之一。

结论 4: 圆柱的体积正好是圆锥体积的 3 倍。 结论 5: 圆柱的体积是等底等高的圆锥体积的 3 倍。

……

同学们实验的结论各不相同，到底哪组的结论对呢？

（各小组纷纷叙述自己小组的实验过程、结论；说明自己小组的准确性，学生的思维处于高度集中状态）。

（5）参与处理信息。

围绕三分之一或 3 倍关系的情况讨论:

我们先来看得出三分之一或 3 倍关系的这几个小组；

请小组代表说说他们是怎样通过实验得出这一结论的？

（请他们拿出实验用的器材，自己展示、验证这个结论。突出他们小组的圆柱和圆锥是等底等高的） 其他小组得出的结论不同，是不是由于实验过程或结论有错误呢？我们也请小组代表说说你们的看法。

（说明他们的过程和结论都是对的，只是他们的圆锥和圆柱不是既等底又等高的）。

总结以上各个小组的看法，我们可以得出什么样的结论？

1: 圆锥的体积等于和它等底等高圆柱体积的三分之一。

2: 圆柱的体积是等底等高的圆锥体积的 3 倍。

3: 我认为第一种说法较合理，强调了圆锥体积的求法。

……

总结：圆锥的体积等于和它等底等高的圆柱体积的 。

3、引导启发，推导公式。

对于同学们得出的结论，你能否用数学公式来表示呢？

因为圆柱的体积计算公式 V=sh；所以我们可以用 1/3 sh 表示圆锥的体积。

其他同学呢？你们认为这个同学的方法可以吗？

那我们就用 sh 表示圆锥的体积。

计算公式：V= sh

（1）这里 Sh 表示什么？为什么要乘 ？

（2）要求圆锥体积需要知道哪两个条件？

学生展开相应回答。

4、牛刀小试，巩固练习。

（1）笑笑家收割了一堆小麦，如图所示，小麦堆的底面半径为 2m，高为 1.5m。你能帮她算算小麦堆的体积是多少吗？

（2）练一练

计算下面各圆锥的体积:

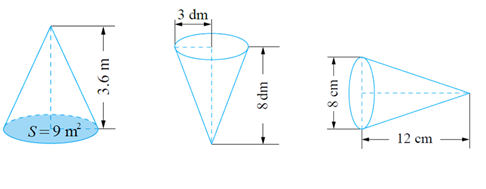
（3）开放性练习 一段圆柱形钢材，底面直径 10 厘米，高是 15 厘米，把它加工成一个圆锥零件。根据以上条件信息，你想提出什么问题？能得出哪些数学结论？（同桌讨论）

5、温故总结，加深理解。

你收获了什么？学生自由展开描述自己本课所得知识内容。

6、知识拓展，课后延伸。 （电脑呈现出动画情境）

小明和小强到底买哪种形状的冰淇淋更合算呢？

7、下课。

8、板书设计：

圆锥的体积

圆锥的体积等于和它等底等高的圆柱体积的三分之一。

V= 1/3 Sh