本帖最后由 容山小学张丽雪 于 2013-9-12 15:47 编辑

三、 实验探究，建立模型

活动一：独立思考，大胆猜测

师：大家都学习过正方形的周长，记得它的公式是吗？

生：C=4a

师：也就是正方形的周长是边长的四倍。

1442

师：老师在正方形里画一个最大的圆，你知道这个圆与正方形的关系吗？

生：正方形的边长等于圆的直径。

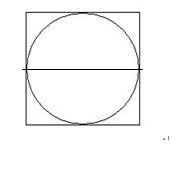
师：刚才又知道圆的周长 与直径有关，结合图，大胆地猜测一下圆的周长与直径究竟有什么关系？

1443

生：圆的周长比直径的四倍小，因为正方形在圆的外面。

生：比 2 倍大一些，因为圆的上半部分曲线比直径长，整个圆周长就比直径的 2 倍长。

师：圆的周长就比直径的 2 倍要大，比直径的 4 倍小，你猜想会是直径的几倍？

生：3 倍左右。

师：要知道猜想得对不对怎么办？

生：验证（做实验）

师：投影出示活动要求。

1、小组分工（四人为一个小组）：两人协作测量（一人拿圆，一人拿尺或纸条），一人观察协助，一人填表，计算。（计算用计算器）

2、填完表后，以四人小组为单位仔细观察表中的数据，你有什么发现？

学生分小组活动、探究。

师：请汇报测量结果。

生：汇报。

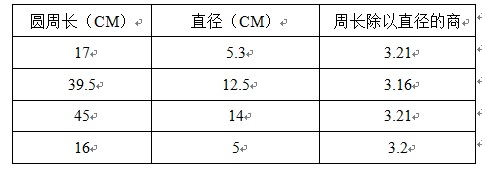
1441

师：观察表格的数据你有什么发现？

生：商的个位都是 3

师：个位是 3，后面还有一些数字。你认为圆周长与直径的关系是？

生：圆周长是直径的 3 倍多些。

师：再看看表格中的周长与直径有什么变化？

生：直径变大，周长也变大，但他们的商几乎不变。

师：大家发现得非常好。实际上周长除以直径的商是一个固定的数。请同学们打开课本 15 页。仔细阅读一下笑笑与智慧老人的话，并说说你知道了什么？

生：圆周长除以直径的商是一个固定的数，叫圆周率，用字母 π 表示，计算时常取 3.14。

师：提到圆周率，就想到了数学家祖冲之，投影出示祖冲之资料。

约 1500 年前，中国有一位伟大的数学家和天文学家祖冲之。他计算出圆周率应在 3.1415926 和 3.1415927 之间，成为世界上第一个把圆周率的值的计算精确到 7 位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间，至少要早一千年。

生：仔细阅读资料。

师：如果用 C 表示圆的周长，d 表示直径，你能说出圆周长的公式吗？

C=πd

师：现在要求一个圆的周长我们要知道什么条件

生：直径。

师：想想还知道什么条件也能求出圆周长？

生：半径。公式 C=2πr

师：知道了公式以后再求圆的周长，我们就不用测量的方法，用公式计算就比较简单了。你能算出这两个圆镜边框的长度吗？学生独立计算。

生：汇报算式结果。

四、解决问题，学以致用

（一）r=5 厘米，求 C=？

（二）选择

1、大圆的圆周率（ ）小圆的圆周率

A 大于 B 等于 C 小于

2、两个圆周长不等，因为它们（ ）不同

A、圆心位置不同 B 直径长度不同 C 圆周率大小不同

3、直径扩大 3 倍，圆周长扩大（ ）倍

图片：