借助 多元 表征 发 展空间观念

—— 新 世 纪 小学 数学六下《 图形 的旋转（ 二 ）》 教 学设计（ 定 稿）

深圳市宝安区张维国教育科研专家工作室 李金荣团队

⑷验证：你能用什么办法验证你同桌画的对不对？

师巡视探究过程，指导个别学生，发现典型做法，安排分享顺序。

汇报预 1：画得对，说不清（鼓励，不打击）

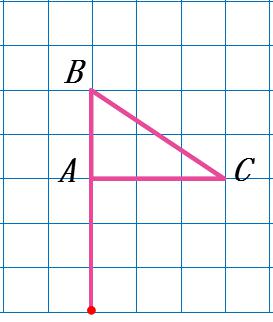
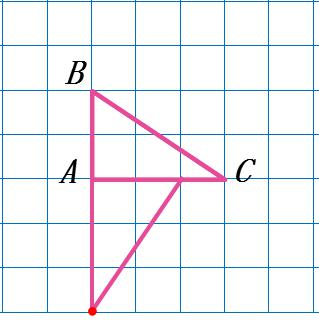
汇报预 2：借助时针（上节课内容）将三角形两条边分别旋转（可追问第三条边怎么不看），迁移旧知，完成旋转过程，从而找到旋转后的正确位置。

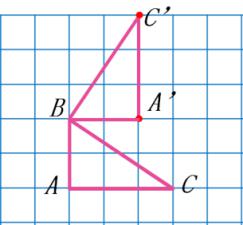
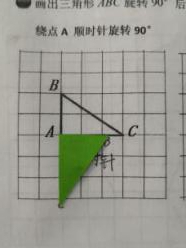
汇报预 3：画得对，说得清，有章有法。如：先画出 AC 绕点 A 顺时针旋转 90° 后的位置，再画 AB 绕点 A 顺时针旋转 90° 后的位置，最后连接成为旋转后的三角形。（一边讲解，一边现场演示，如下图：）

汇报预 4：绕 B 点逆时针旋转 90 度是特别容易出错的，展示错例，验证结论，分析原因，寻找方法。（寻生上台借助实物验证，同时顺势引导：实物除了验证，其实还可以帮助我们画图）

8384 8385 8386 8387 8388

预 2 预 3 预 4

思考：在刚刚分享的这些方法中，你比较喜欢哪一种？为什么？渗透在没有学具的情况下，要找出关键的线段分别旋转之后再画出图形？有没有只找一条关键线段就能正确画出图形的？分享一下经验。

出示三角形板贴，问：哪条线段比较关键？揭示突出关键线段，得出结论：与旋转中心相连的线段，往往就是关键线段）；板书：与旋转中心相连的线段 —— 关键线段。

若时机成熟，可以追问思考：刚刚的三角形旋转中，是不是一定要找到两条关键线段呢？

〖设计意图〗 相较于任务一，第二个任务的三角形虽然表面上看并不复杂，实际上学 生可借助的 “关键 线段 ” 变成了两条，与此同时，干扰因素也就相应地增加。活动中，我设计了想 象 —— 操作 —— 交流 —— 验证 —— 分享等环节，目的就是通过流程式的探究过程充分调动学生的感观体验，让旋转这一运动表象深入人心。尽管是六年级的学生，空间观念的建立依然是差异的、不均衡的，所以还是要提供实物三角形供他们验证结果或是表征过程。当然，对于只找一条关键线段就能根据部分与整体的关系正确画图的同学来说，应该是空间感极强的表现，让他们分享，是为了让更多学生建立图形自身的内部空间感。