教案三稿

【教学过程】

一、情境导入，引发思考

（课件出示下图）

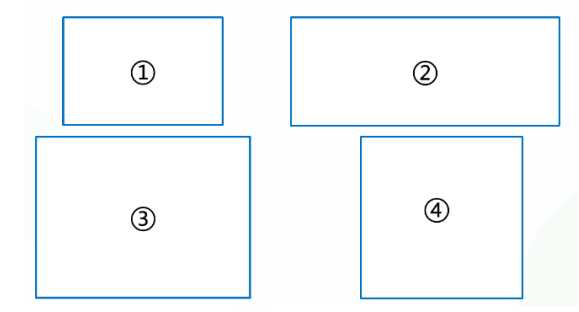
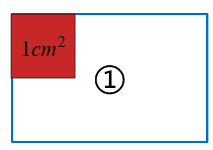
师：今天老师带来了 4 个图形，想请同学们帮他们比比大小。你们愿意吗？比大小就是比什么？面积是什么？今天这节课我们就来研究长方形的面积。

【设计意图】通过师生谈话，开门见山引出 4 个图形，这 4 个图形隐藏着宽相同，长越长，则面积越大。即长方形的长影响着面积的大小。引导学生明白比较长方形的大小就是比较长方形的面积，为进一步认识面积，探究长方形面积公式做好铺垫。

二、小组合作，寻找联系

活动一：铺方格，量①号图形的面

1. 想办法量

师：①号图形的面积到底有多大？怎么量

2. 操作活动

引导学生拿出 1㎠的小正方形铺一铺。

3. 汇报交流

（1）铺满

一行铺 3 个，可以铺 2 行，一共用了 3×2=6 个小正方形，所以 1 号长方形的面积是 6㎠。

（2）铺部分

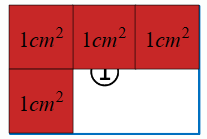
一行铺 3 个，可以铺 2 行，可以推想铺满能铺 3×2=6 个小正方形，所以①号长方形的面积是 6㎠。

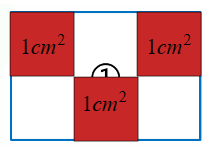
推想要将①号长方形铺满，需要 3×2=6 个小正方形，所以①号长方形的面积是 6㎠。

（3）只铺 1 个

生用 1 个 1㎠的小正方形平移量。

师：（课件动态演示做标记的过程）我们在屏幕上再看一下。

师：这几种铺的方式不一样，但都得到了它的面积是 6㎠，想象这 6 个小正方形是怎么铺的？

预设：每行都是 3 个，铺了 2 行。

【设计意图】测量①号长方形面积的大小时，引导学生借助面积单位，从铺满 -- 铺部分 -- 只铺一个，对比不同铺法，引导学生感悟长方形的面积就是看长方形中有多少个 1㎠的面积单位，在面积单位逐步减少的过程中，渗透每行个数、行数和面积单位总个数之间的关系。

活动二：看标记，探究长方形面积

1. 看标记，估面积

（1）6㎠

师（课件出示下图）: 现在一个小正方形都没有了，留下标记，你还能看出它的面积是多少吗？你是怎么看的？

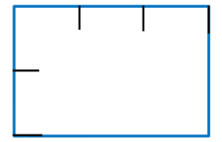
预设：一行铺 3 个小正方形，铺 2 行，共有 6 个小正方形，也就是 6㎠。

（2）8㎠

师 (课件动态演示变化过程）：它的面积是多少？你是怎么看出来的？

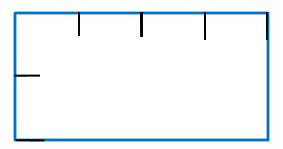
预设：一行要铺 4 个小正方形，铺 2 行，一共铺 8 个，所以长方形的面积是 8cm²。

（3）10㎠

师 (课件动态演示变化过程）：它的面积是多少？你是怎么看出来的？

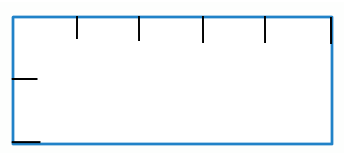
预设：要把这个长方形铺满，一行要铺 5 个小正方形，铺 2 行，一共要铺 5×2=10 个，所以长方形的面积是 10cm²。

师：对比这 3 个图，你认为面积变大的原因是什么？每行个数对应长方形的什么？

小结：看来，长能够影响长方形面积的大小。那宽呢，我们继续研究。

师：对比，你又发现面积变化的原因是什么？

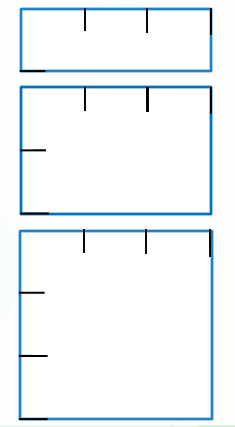
宽增加就是什么在增加？

小结：看来宽也能影响长方形面积的大小

4. 汇报数据

长、宽和长方形的面积到底有什么关系？

结合三幅图让学生汇报长、宽、面积的数据。

5. 将二维面积度量转化为一维符号运算

师：，长 8cm，宽 5cm, 面积是多少？

长 8 让你想到了什么？宽 5 让你想到了什么？

6. 长方形的面积

长方形面积可以怎么算？

计算长方形的面积就是计算小正方形的总个数

【设计意图：从铺方格 -- 记标记 -- 推理想象 -- 归纳公式，在过渡中让孩子感悟到长方形面积与面积单位总个数，长与每行个数，宽与行数之间的对应关系，进而明白长方形面积 = 长 × 宽计算的道理，在小组合作与探究中培养学生符号化意识。】

活动三：用尺子量面积

1. 想方法度量②号长方形的面积

（1）猜想方法

师：现在请你收起小正方形，怎么得到②号长方形的面积？引出尺子。

（2）活动操作

（3）交流汇报

2. 度量③图形

3. 度量④号图形，得出正方形面积公式

④号图形是一个正方形，面积计算是 3×3=9cm²。

（4）对比迁移

引导学生回想，长方形和正方形面积的探究都是在数小正方形的总个数，在数面积的过程中，迁移出正方形面积的公式，引出长方形和正方形的关系。

4. 字母表达

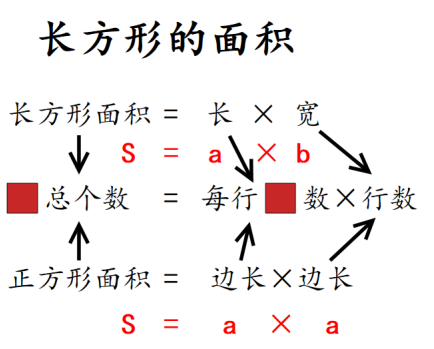
两个面积公式都有一种更简洁的表达方式，字母表示。通常用 S 表示面积，a 表示长，b 表示宽。S 等于 a 乘 b。正方形的面积 S 等于 a 乘 a。

5. 比较面积

师（课件出示①②③④号图形）：现在你能比较出 4 个图形的面积了吗？（指生汇报）

【设计意图】从数方格 -- 做标记 -- 尺子量既是度量工具的逐步优化，又是符号意识增强的充分体现。通过对比长方形和正方形数方格求面积的方法，认识到这种方法既适合长方形面积的探究，又适合正方形面积的探究，在迁移中引导学生得出正方形的面积公式，再一次感受正方形与长方形的关系。

学生能在迁移中体会到正方形是一种特殊的长方形，同时还能体会到用长 × 宽计算它们的面积，这种符号化的表达具有学习上的一致性。学生迁移的学习能力在潜移默化中得到提升。

三、学以致用，计算面积

1. 运用面积公式解决问题

你会计算长方形草地、正方形花坛的面积吗？（单位：米）

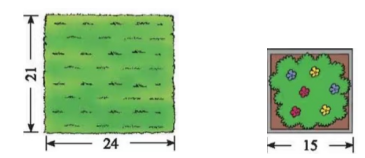
【设计意图】他们不仅体会到数学与生活的联系，还能学以致用。从公式的表达到公式的运用，进一步让孩子感受面积公式符号化表达的简洁性。

四、拓展提升，变换图形

1. 画面积为 6cm² 的图形

师（课件出示①号图形）：还记得它吗？面积是 6cm²，6cm² 的图形一定长这样吗？还会长什么样呢？请你想一想，用彩笔至少画 3 种不同的图形。

2. 回顾迁移

今天我们借助 1cm² 的小正方形作为面积单位，不仅得到了长方形的面积公式，还得到了正方形的面积公式，我们可以用这种方法可以去度量平行四边形、三角形的面积吗？

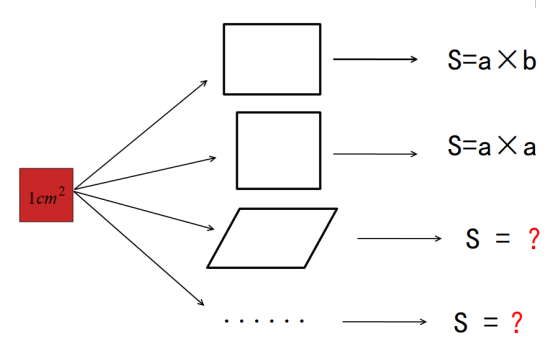
【设计意图】给学生知识，不如给学生知识结构，长方形面积公式的正向利用，每个孩子可能都会。但看数据画图形，不仅体现了公式的逆向推导，还渗透了数形结合的思想，引导学生在应用公式的基础上又提升了学生思维。画面积是 6cm² 的图形，开放了学生的思维，面积一样，形状各异。面积单位度量是探究图形面积的基本方法，长方形面积公式又是其他图形面积公式推导的根基，将长方形面积探究经验迁移到其他图形面积探究之中，逐步渗透优化的符号意识，凸现符号意识的重要性。

五、总结升华，知识迁移

师：以前我们量周长，选用的是长度单位，用的工具是尺子。今天我们量面积，选用的是面积单位，用的工具是 1cm² 的小正方形、尺子。有人说，尺子可以度量天下， 你觉得尺子还能量什么？留给大家思考。

【设计意图】从周长到面积，不仅是概念本身的变化，还有度量方式的不同，引导孩子认识到量面积可以用面积单位度量，也可以通过降维转化用尺子度量，体会二维面的度量和一维线的度量之间的对应关系，同时孩子能体会到尺子度量的便捷性、实用性。

板书设计