【教案三稿】

《平行四边形的面积》教学设计

一、复习导入，提出问题

师：同学们，我们已经学过了哪些平面图形的面积？请大家回忆我们是怎么得到这些图形的面积的？今天我们一起来探索一个新的平面图形的面积。

二、面积度量，探索新知

1，抛出问题，师：为了让我们的学校环境更加优美，学校决定增加我们的绿化面积，要在这块空地上铺草坪，请问：这块空地是什么形状？要求空地的面积就是求什么？点题，板书（平行四边形的面积）

2、大胆猜想

如何求这块空地的面积？请你大胆猜想。

学生可能会有以下方法：

方法 1：我认为平行四边形的面积是 6×5=30（平方米），因为长方形的面积是长乘宽，所以平行四边形的面积可以是两条临边的长度相乘。

方法 2：我认为平行四边形的面积可以用底乘高来计算，6×3=18（平方米）。

方法 3：可以借助透明方格纸来数一数。

他们的猜想是否正确呢？我们一起来验证。

【设计意图】结合铺草坪的情境，鼓励学生思考如何求平行四边形面积，创设认知冲突，在多种思考中引导学生体会度量的必要性，为接下来的深入探究埋下伏笔。

3. 各种方法验证。

（一）借助方格纸数一数，比一比。

1. 估一估。

方格纸中的一个小方格代表 1 平方米，估一估，长方形和平行四边形的面积大约是多少？

2. 数一数，比一比。

请同学们数一数，比一比，在学生操作后上台展示。

学生可能呈现的方法如下：

方法 1： 一格一格的数

方法 2： 测量计算法

【设计意图】通过数一数，比一比，让学生体会借助方格纸能够一格一格的 “数” 出图形的面积，渗透面积度量的有限可加性和正则性。同时验证得出：用邻边的长度相乘求平行四边形的面积得方法是错误的。

（二）用割补法求平行四边形的面积。

你还有其他方法求平行四边形的面积吗？认真想一想，请拿出借助学具袋 2（一把安全剪刀、两个完全相同的平行四边形）独立完成。

1. 教师巡视，指导学生剪拼。

2. 小组交流。

3. 学生上台展示，交流方法和收获。（引导学生进行相互评价）

首先，用三角板和铅笔画出平行四边形的一条高。然后，用剪刀沿高剪开，就能得到一个三角形和一个梯形。最后，将三角形向右平移，就把平行四边形转化为一个长方形。

【设计意图】通过剪拼、平移、转化等具体操作，渗透面积度量的 “有限可加性” 和 “运动不变性”。

4. 把平行四边形转化成长方形，拼成的长方形与原来的平行四边形的面积有什么关系？

师反问：转化前后，平行四边形的什么变了，什么没变？

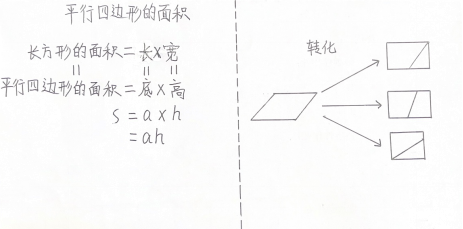
拼成的长方形的面积等于原来平行四边形的面积（板书），拼成的长方形的长相当于原来平行四边形的底（板书），拼成的长方形的宽相当于原来平行四边形的高（板书）。因为长方形的面积等于长乘宽，所以平行四边形的面积等于底乘高（板书）。

5. 谁能完整的说一说：怎样求平行四边形的面积？

（1）学生上台边指边讲。（引导学生进行相互评价）

拼成的长方形的长相当于原来平行四边形的底，拼成的长方形的宽相当于原来平行四边形的高。因为长方形的面积等于长乘宽，所以平行四边形的面积等于底乘高。

（2）同桌两人相互指一指，说一说。

【设计意图】通过反复梳理，引导学生准确找出转化前后两个图形之间的联系。在指一指，说一说，反复对比，相互讲解中强化平行四边形的面积公式推导过程。

（4）用字母表示平行四边形的面积公式。

如果我们用 S 表示平行四边形的面积，用 a 和 h 分别表示平行四边形的底和高，那么，平行四边形的面积公式可以写成：S=ah。

（4）问题追问，强化公式

①根据推导，要求平行四边形的面积，需要知道什么？

②知道了平行四边形的底和相应的高，怎样求平行四边形的面积？

（三）利用公式，解决问题。

你能求出这块平行四边形空地的面积吗？在练习本上独立完成。

6×3=18（平方米）

答：这块空地的面积是 18 平方米。

三、巩固练习，强化度量

生活中存在着许多与平行四边形的面积有关的数学问题。让我们一起去看一看吧！

1.

求平行四边形的面积

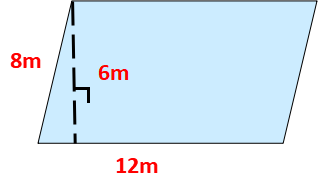
【设计意图】引导学生明白对应的底要乘以对应的高才能求平行四边形的面积。

2. 强化公式推导，独立完成平行四边形的面积度量。

（1）画图并与同伴说一说，平行四边形的面积公式是怎样得到的？

（2）量一量并计算下面平行四边形的面积。

【设计意图】进一步巩固平行四边形面积的计算。设计这道题，能让学生明白测量的对象需要是一组对应的底和高。测量时允许有误差。

3、一块平行四边形街头广告牌，底是 8.5m，高是 5.4m。要粉刷这块广告牌，每平方米要用油漆 0.5kg，至少需要准备多少千克油漆？

【设计意图】让学生体会可以用所学知识解决生活中的实际问题。

四、全课小结

通过本节课的学习，你有什么收获？

五、板书设计