《方程》教学设计

辽宁省锦州市教师进修学校基地 曲雯霞

教学内容 ：北师大版小学数学四年级下册第五单元《认识方程》第三课时内容。

教材分析：

《认识方程》是学生学习代数初步知识，教材运用丰富的问题情境，引导学生用语言描述具体情境中的等量关系，并用含有未知数的等式表示，在此基础上引导学生找出这些含有未知数的等式的共同特征，了解方程的含义。

《方程》是在学习用字母表示数、等量关系的基础上进行学习的，通过本课的教学，学生了解方程的含义，或用方程表示简单的数量关系，本课的教学在学生日后学习等式的性质、了解方程及运用方程解决简单的实际问题的过程中，起着承上启下的作用，它是学生学习用方程解决问题的起始课，在本单元中具有重要地位。

学情分析：

《方程》对于儿童来说是一堂全新数学概念课，是算术思维的一种提升，是数的认识上的一个飞跃，在用字母表示未知数的基础上，是学生解决实际问题的数学工具，从列出算式发展到列出方程，从未知数只是所求结果到未知数参与运算，学生的思维空间增大，这是学生数学思想方法上的一次飞跃，它将使学生运用数学知识解决实际问题的能力提高到一个新的水平。

教学目标 ：

1. 结合具体情境，了解方程的意义，会用方程表示简单情境中的等量关系。

2. 经历将现实问题抽象成等式与方程的过程。积累将等量关系符号化的活动经验。

3. 在丰富的问题情境中感受生活中存在大量的等量关系，体验数学与生活的密切联系。

4. 教学重点：

了解方程的意义，会用方程表示简单情境中的等量关系。

教学难点：

将现实问题抽象成等式与方程的过程，积累将等量关系符号化的活动经验。

教学准备： 课件

教学过程：

一、谈话激趣，导入新知

1. 谈话导入：

（出示跷跷板图）同学们，这是什么？玩过跷跷板吗？

【设计意图：数学知识来源于生活，数学教学应以学生的认知水平和已有经验为基础。“跷跷板” 作为儿童生活中较为熟悉的一种游戏活动，有着与天平相似的工作原理，以它作为一个导入新知的话题，既可以激起学生的兴趣，又为后续的学习做了很好的铺垫。】

2. 初步感受 “不平衡” 和 “平衡”：

淘气和笑笑也想玩跷跷板，你觉得有哪几种可能？为什么？（给出体重）此时跷跷板会怎么样？（出示书包及其质量）如果笑笑背上书包，跷跷板会怎样？你能用式子表示出跷跷板现在的状态吗？

3. 认识等式：

（板书算式 40+2=42）认识等式：算式左右两边相等的式子叫等式（板书：等式）。此时的等号就像一根保持平衡的跷跷板（师做手势）使左右两边的质量一样重，等号虽小，作用可不小！

你还能写出几个等式吗？（师板书）

【设计意图：学生从直观情境出发，经历从自然语言描述事件到数学语言描述的过程，体会等号左边的算式和右边的数表示两个相等的量，它们的地位是均等的，突破对原有等号作为表示运算结果时出现的符号认识。】

二、 探索交流 构建新知

（一） 初探 “天平图”

1. 过渡：在我们的生活中有一种工具，和跷跷板的原理差不多，请看（出示天平图）。

2. 简单了解天平秤（托盘 指针 砝码等）。

3. 出示 “天平图” 找等量关系：

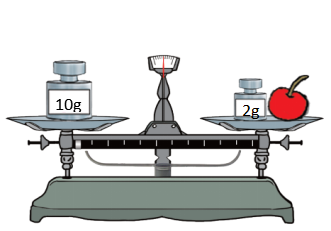
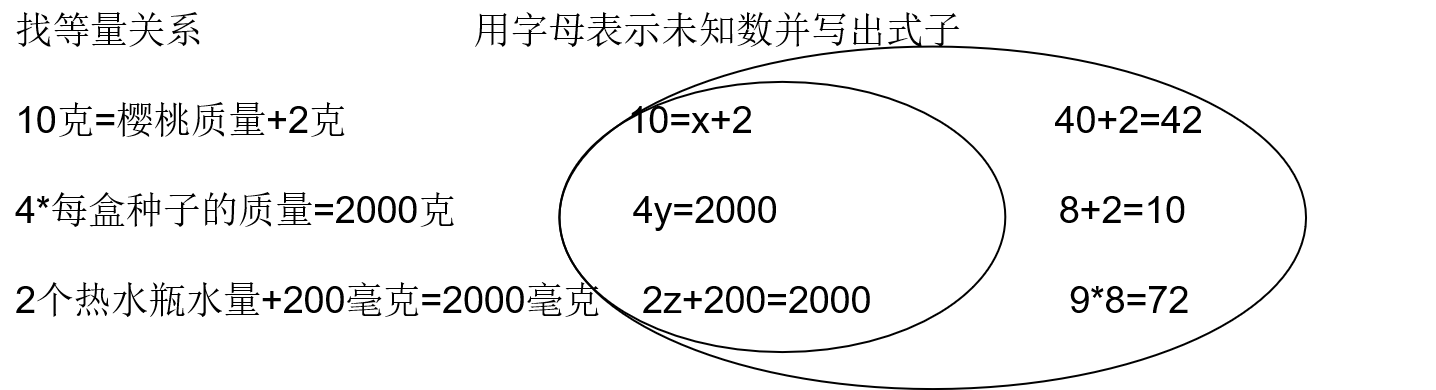
请大家仔细观察，此时天平左边托盘有什么？右边呢？现在天平左右两边是否平衡？说明什么？你能找出图中的等量关系吗？（粘贴：找等量关系）

预设：10g = 樱桃的质量 + 2g   或者  樱桃的质量 + 2g=10g （粘贴：10 克 = 樱桃质量 + 2 克）

你是怎么想的？指名交流（想法正确，给予肯定）。

4. 用字母表示未知数：在这个等量关系中有一个未知数（板书：未知数），是谁？等量关系这样写你觉得怎么样？你想怎样表示这个未知数？为什么想到用字母表示？用字母表示数有什么优点？（粘贴：用字母表示未知数）

学生尝试用字母表示樱桃的质量，用式子表示天平中的等量关系。

预设：x+2=10    或 10=x+2  （都可以） 可以在简洁些吗？（单位可以省略不写）

（板书：10=x+2）

【设计意图：引导学生发现它们中都含有一个未知数，而且未知数是用文字表示的，写起来比较麻烦，我们在本单元第一课学习了《用字母表示数》，体会用字母表示未知数的简洁性，渗透符号意识。】

5. 过渡：你们的这种想法跟一位数学家想到一块去了。

介绍古希腊数学家丢番图，了解符号发展的历史。

【设计意图：了解丢番图，感受符号的作用，培养符号意识】

6. 小结：回忆一下，我们是如何将 “天平图” 用这样简洁的等式表示出来的？（先找等量关系 ---- 再用字母表示未知数并写出式子）

（二）合作完成 “种子图” 和 “倒水图”

1. 你能用这样的方法挑战下面的任务吗？（出示 “种子图” 和 “倒水图”）

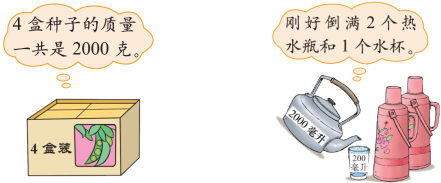
【设计意图：通过对多个现实情境中等量关系复杂程度层层递进的方程描述，体会方程是刻画现实世界的有效数学模型，其思想核心是用数学符号表达两件事情的等价。】

2. 出示小组合作学习要求：

（1）先说一说图中的等量关系是什么；

（2）再说清楚你们小组是怎样得到这一等量关系的；

（3）用含有字母的式子表示等量关系

（4）小组其他成员及时补充，其他组成员可以提出疑问或建议。

3. 小组内思考与交流，在学习纸上记录自己的思考过程，师巡视指导。

4. 师引导全班交流：你能像刚才一样，把种子图看成一架天平，找到左边和右边是什么吗？

全班交流：组内成员补充，组外同学提出建议或质疑。

【设计意图：在交流中发展学生观察、抽象、质疑和表达等能力。交流中不仅要呈现出正确的等量关系，还要呈现出不一样的等量关系，引导学生观察和分析，辨别出等量关系的对与错。】

等量关系的预设：

①每盒种子的质量 * 4=2000 克或 2000 千克 = 4 * 每盒种子的质量  

② 4 盒种子的质量 = 2000 克（追问：4 盒种子的质量如何用算式表示？）

③2000 毫升 = 每个热水瓶盛水量 * 2+200 毫升

④2 个热水瓶的盛水量 + 200 毫克 = 2000 毫克

注意：等量关系可能会出现：“2000÷4 = 每盒种子的质量” 这样的写法。追问：这样的等量关系对吗？为什么？（及时反馈：同一个问题，有不同的等量关系；一般情况下，不把未知数单独放在一边。）

5. 认识方程：

（1）方程意义：我们刚才列出的这三个等式。请你观察这三个等式，它们有什么共同的特点？

在学生发现的基础上明晰：像 10=x+2， 4y=2000…… 这样含有未知数的等式叫方程。（完善板书）反问：什么是方程？你觉得方程需要具备哪些条件？

（2） 辨析等式与方程之间的关系：

师：谁能把黑板上的所有等式都圈出来？（学生上前来圈一圈）

师：谁能用一句话概括等式与方程的关系。（方程包含在等式里面；方程一定是等式，等式不一定是方程。）

【设计意图：描述现实世界中的数量关系的式子有很多种，让学生从常见的关系中通过观察、比较、分类、抽象、概括逐步分化出方程的概念，明确概念的内涵与外延，自主构建起对概念本质特征的认识。】

三、 巩固练习，解决问题

（一）基础练习：

1. 你能像这样再说出一个方程吗？学生尝试，师板书，全班评价。

2. 辨析题：老师也写了几个式子，大家看看我写的是不是方程？出示课件，辨析是否是方程。

（二）巩固练习：

生活处处有方程，在我们的衣食住行中，方程能帮助我们解决很多问题，我们一起感受一下吧。

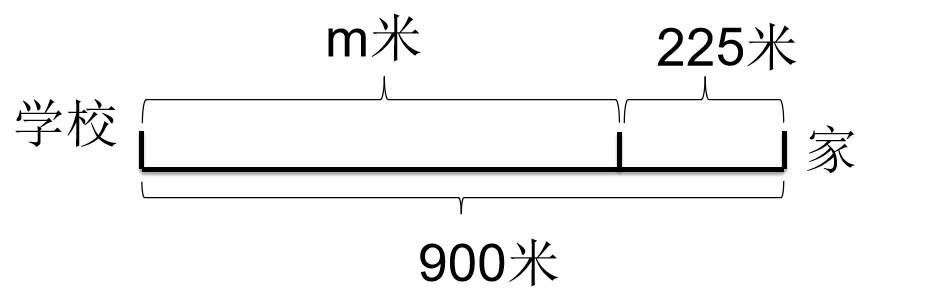
出示衣、食、住、行方面的 4 道练习题：你能列出方程吗？（食：天平为媒介呈现素材；行：数形结合图示法呈现素材；衣：插图文字呈现素材；住：纯文字呈现素材）。

食：

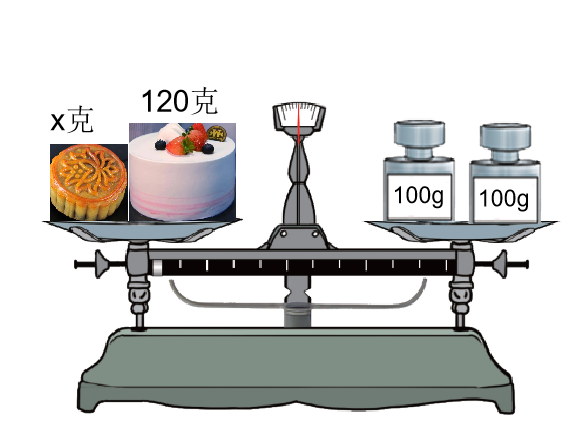
行：

衣：

住：

【设计意图：仅靠天平来表示生活中的相等关系太单调了，由天平入手，练习的呈现难度由浅入深，呈现形式可以多样一些，但更要注意重视学生能否从素材中迅速找到相等关系，列出方程。】

（三）拓展练习：我来编方程。

四、 总结、思考、共勉

（一） 谈收获，了解方程的前世、今生、后世。

（二） 开放性思考：为什么要学习方程？

【设计意图：数学学习活动应引发学生的数学思考，为什么要学习方程？学习方程有什么作用？怎样列出方程？等等，都是引导学生在学习过程中要善于发现问题、提出问题、从而培养学生的问题意识。】

（三） 科学家爱因斯坦在谈成功的秘诀时，写下了一个公式：成功 = X+Y+Z 他解释道：

X 代表艰苦的劳动，Y 代表正确的方法 ，Z 代表少说空话，现在你知道怎样才能成功了吗？老师把这个公式送给正在努力中的你！加油！

五、板书设计：

方程

含有未知数的等式叫方程。