教学设计二稿

一、教材分析

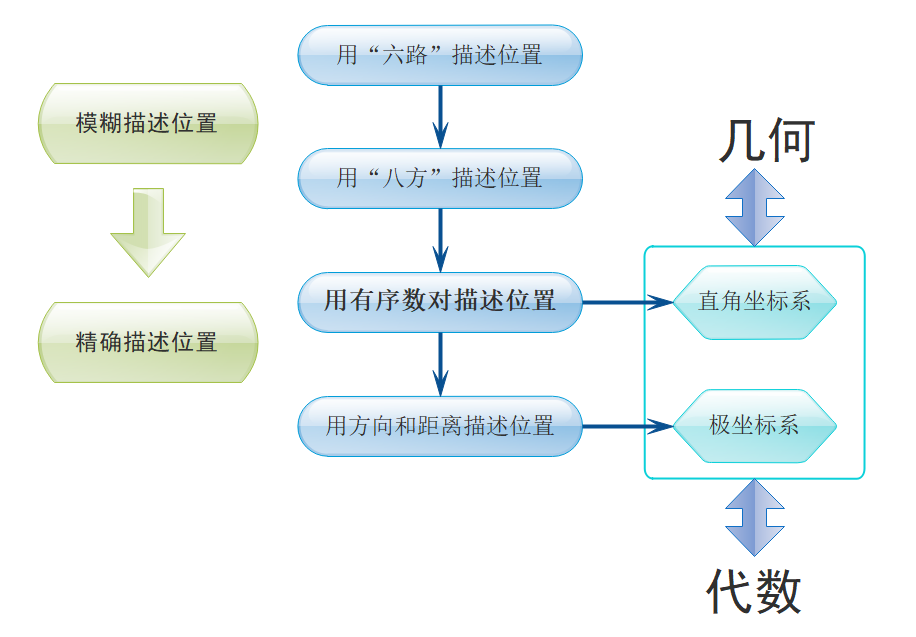
《确定位置》这节课是北师大版教材四年级上册《方向与位置》单元中的内容，属于 “图形与几何” 领域中 “图形与位置” 部分的内容，是在学生已经掌握了 “六路”（上、下、前、后、左、右）和 “八方”（东、南、西、北、东南、东北、西南、西北）的基础上学习的一种描述物体位置的方法 —— 用有序数对确定位置。用有序数对确定位置，是描述物体位置从模糊到精确的重要一步，是第一次引入数学结构描述物体的位置，具有很重要的承前启后作用。用有序数对刻画物体位置的思想方法，为五年级学习用方向和距离描述物体位置乃至中学的直角坐标系和极坐标系做了关键的铺垫和迁移基础。

有序数对实质上就是坐标，坐标把几何图形转换成了代数结构，从用方位词描述物体位置到用代数结构描述位置凸显了符号意识的发展，经历将实际问题抽象成数学模型并进行解释的过程，也积累了运用符号的数学活动经验，感悟了符号化的数学思想，提升了符号意识。用有序数对确定位置，将相互分离的 “数” 与 “形” 统一起来了，有利于感悟数形结合的数学思想，为学生将来直观理解直角坐标系，进一步学习各类坐标系做准备。有序数对将几何学习的视野拓宽到学生生活的空间，使学生更好地理解自己所处的世界，加强了对空间方位与位置关系的感知，发展空间观念。

二、学情分析

学生在之前已经学习了用 “六路”（上、下、前、后、左、右）描述一维空间的物体相对位置，也会用 “八方”（东、南、西、北、东南、东北、西南、西北）描述物体的相对位置。这些前置的学习经验为学生在二维平面上进行位置确定做了知识上的储备。《确定位置》这节课与学生的生活联系紧密，学生在课前就已经积累了丰富的生活经验。学生在日常生活中也会用类似 “第 2 组，第 4 个” 的方式描述自己的座位，丰富的生活经验为教学提供了有利的支撑。

三、教学目标分析

（1）结合具体的情境，体会用数对确定物体位置的必要性，感悟符号化的思想，提升数学符号意识。

（2）经历由实物图到点子图的抽象过程，体会数学抽象在问题解决中的价值所在。

（3）经历数对生成的过程，重走笛卡尔探索的足迹，感悟古人智慧的光芒。

四、重点难点分析

（1）教学重点：用数对确定位置的必要性；数对生成的过程

（2）教学难点：数对生成的过程

五、教学流程预设

（一）情境导入，任务驱动

同学们，学校将于过段时间组织一次线下家长会，你会怎样向爸爸妈妈介绍你的座位呢？请将你的方法写在学习单上。

（二）多样描述，确定位置

搜集部分学生的作品，有梯度地进行展示。

（1）先展示一维表示方法

生 1：我是张三的同桌。

追问：张三坐在哪？

生 2：我在李四的后面。

追问：李四坐在哪？

（2）再展示二维表示方法

生 3：我在第 3 排第 4 个。

师：其他同学有什么问题吗？可以提问。

生 4：第 3 排到底是从前往后数，还是从后往前数的。同样的，第 4 个是从左往右数，还是从右往前数呢？

生 3：从前往后数，我在第 3 排，从左往右数，我在第 4 个。

师：要提前规定一下数的方向。

（3）最后展示类数对表示

生 5：3F

生 6：（3,4）

生 7：（4,3）

师：大家看懂了吗？谁来说一说。

生：……

（4）交流研讨，对比多种不同的表示方法

师：对比这些不同的表示方法，你最喜欢哪种呢？为什么呢？小组内交流讨论一下。

组织学生分享不同的观点。

（三）呈现数对，溯古探源

师：同学们给出的表示方法都是合理的，都能很清楚的表示出我们的位置。让我们来看看大数学家笛卡尔会用什么样的表示方法呢？

（微视频介绍笛卡尔是如何从蜘蛛结网中找到灵感，从而用数对表示物体位置的，同时，也要介绍一下数对的优势所在）

师：同学们的这些表示方法也都是对的。数学是一门交流沟通的语言，随着时间的推移，人们选择了笛卡尔的这种表示方法，并一直沿用至今。

（四）应用数对，深化理解

师：那我们就来试试笛卡尔的这种方法吧。首先，将我们教室的座位图也结成一张蜘蛛网。

师：根据前面的讨论，我们要怎样才能表示自己的位置呢？

生 8：需要先约定方向，从那边开始数？

师：那我们就一起来约定一下，从左往后数，第 1 列，第 2 列……，从前往后数，第 1 行，第 2 行……

师：那现在你会用笛卡尔的方法表示一下自己的位置了吗？在学习单上动手试试吧。

教学组织：组织几个同学将自己的方法写在黑板上，并说一说自己的想法。

（五）延伸数对，开拓视野

师：大家都记住了自己所在座位对应的数对了吗？

师：那老师来考考你是否真的都记住了。老师出示一个数对，这位同学立刻站起来，并用 “第几列，第几行” 的形式说出自己的位置。

师：（1,5），（2,5），（3,5），（4,5），（5,5），（6,5）（出示一个数对之后，前面出示的数对不要丢失，颜色变浅即可）

师：（4,1），（4,2），（4,3），（4,4），（4,5），（4,6）

师：观察这些数对，有发现什么规律吗？

生 9：第一组数对的第 2 个数都相同，都是 5，他们的座位都在一条直线。第二组数对的第 1 个数都相同，都是 4，他们的座位也是在一天直线上。

师：这个规律发现的真好！让我们来听听笛卡尔的想法。

（PPT 上动画呈现笛卡尔的点线成形，心形线，并配音：如果在这个平面建立坐标系，那么就可以用一个式子来表示更多美丽的图形了）

（六）回归生活，升华数对

师：今天，我们学习了有序数对。其实生活中处处都有着数对的影子，请同学回想一下有哪些？

PPT 呈现出电影院座位、火车座位、海中航船的位置（东经 72°，北纬 58°）

师：这些场景，虽然不是直接用数对（3,4）这样的形式表示的，但是其背后的思想都是一样的，都是用 2 个数组成的数对确定了二维平面的位置。

师：确定二维平面的位置需要 2 个数，如果是三维空间呢？这个问题留给同学们好好思考。

（七）课堂回放，再遇数对

师：最后，我们一起来回顾一下我们是怎样学习认识数对的？

师：马上要开家长会了，我们要给爸爸妈妈介绍自己的座位。同学们的方法各种各样，大家的方法都可以清晰的向爸爸妈妈传达座位信息。后来，我们了解到笛卡尔从蜘蛛网上找到灵感发现坐标系的故事，我们沿着笛卡尔的足迹，用他的方法表示了我们的座位。最后，我们还知道，如果建立了坐标系，很多美丽的图形都可以用式子表示出来了。