《邮票的张数》教学设计第三稿

黑龙江省大庆基地（二）队

大庆市萨尔图区东风新村第四小学 姜世卓

【 教学内容 】

北师大版数学五年级下册第七单元第一课时第 69 页

【教材分析】

《邮票的张数》是新世纪小学数学（北师大版）五年级下册第七单元 “用方程解决问题” 的第一课时。本课是学生学习了字母表示数、等量关系、初步认识方程、会用等式的性质解决简单方程，会列方程解决简单的实际问题的基础上进行教学的。教材创设了 “邮票张的数” 的问题情境，情境中提供了两条信息，并设计了四个问题。第一个问题是解读问题，启发学生思维，寻找解决问题的途径；第二个问题是分析数量关系，从文字描述、画方块图解释姐弟之间的邮票张数的关系；第三个问题是根据等量关系，列方程解决问题，借助淘气的思考说明形如 aχ±χ=b 方程的解法。第四个问题是变换问题中的信息提出新的用方程解决的问题。通过本课学习，学生经历将现实问题抽象为方程的过程，积累将现实问题数学化的经验，会用方程解决含有两个等量关系的简单实际问题，学会解形如 ax ± x=b 的方程 进一步理解等量关系，感受方程的思想和价值，发展抽象能力和符号感。

【学情分析】

学生的学习起点 ：学生认识方程后， 前面学生学习的方程解题都是只有一个未知数和一个等量关系。

学生的学习难点： 本节课出现了两个未知数和两个等量关系，即弟弟的邮票张数 ×3 = 姐姐的邮票张数，姐姐的邮票张数 + 弟弟的邮票张数 = 180 张。现实中，受已有认知和思维发展水平的影响，学生对两个等量关系与列出的方程之间的链接停留在混沌状态，而要从一个等量关系来表示两个未知数，另一个等量关系来列方程，促进符号语言的准确运用，是认知上的难点。怎样突破难点：数形结合，感知符号意义，读懂符号价值，发展符号意识；运用讨论交流，解决两个未知数问题，强化符号应用，深化方程求未知数的数学模型，实化符号化思想的培养。

【学习目标】

1. 通过解决姐弟二人的邮票张数问题，学会解形如 ax+ x=b 这样的方程，进一步理解方程的意义。

2. 会分析简单实际问题中的数量的相等关系，会用方程解决简单实际问题。

【教学重点】

通过解决姐弟二人的邮票张数问题，学会解形如 ax+x=b 这样的方程，进一步理解方程的意义。

【教学难点】

会分析简单实际问题中的数量的相等关系，会用方程解决简单的实际问题。

【教具准备】 多媒体课件

【教学过程】

一 、创设情境  激发兴趣

师：观察情境图 看清 并 说清 ，你发现了什么数学信息？根据数学信息你又能提出什么数学问题？

生：姐姐的邮票张数是弟弟的 3 倍。

生：我和姐姐一共有 180 张邮票。

生：姐姐有多少张邮票？

生：弟弟有多少张邮票？

生：弟弟和姐姐各有多少张邮票？

二、合作学习  构建新知

（一）弟弟和姐姐各有多少张邮票？尝试用方程解决。

师： 下面，我们一起来解决 “弟弟和姐姐各有多少张邮票？” 这个数学问题。

1. 引导学生完整地描述问题，明确所要解决的问题是什么。

师：你能带着数学信息把数学问题完整的说一遍吗？

生：姐姐的邮票张数是弟弟的 3 倍，我和姐姐一共有 180 张邮票。弟弟和姐姐各有多少张邮票？

师：谁能像他一样再说一遍。

2. 尝试让学生想清该如何解决问题，并组织学生进行交流说清。

师：怎么解决这个问题？你有什么想法？独立思考 想清 ，然后和你的同桌小声的 说清 。

师：怎么样？谁想说说你的想法？

生：好习缺少条件，没有思路。

生：用算术方法解答。

生：学生会提出用方程解决。

教师指导：如有用算术方法解决的学生，教师先让学生展示算术方法。

3. 提出用方程解决问题的要求。

师：他借助题中的数量关系，求出了弟弟和姐姐各有多少张邮票。其实像这样的问题，也可以尝试用方程来解决。

教师指导：在交流中，关注学生不同的分析问题思路，对学生不同的思路，只要合理，教师就给予肯定。同时，对不科学的分析思路，将采用延迟评价的方式，在后续解决问题的过程中引导学生进行自我调整。

【设计意图：根据情境中提供的信息，结合学生提出的数学问题，培养学生完整描述问题的习惯并启发学生思维，寻找解决问题的途径，唤醒学生的符号意识。】

（二）找出题中的等量关系，并进行表示。

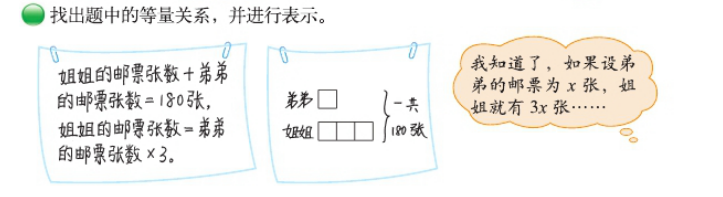
师：用方程来解决问题，想一想我们要先干什么？

1. 学生独立思考想清并写清等量关系。

师：请独立思考 想清 ，然后把等量关系在练习本上 写清 。

2. 全班交流说清。

师：谁想跟大家交流一下自己的想法？

生：姐姐的邮票张数 = 弟弟的邮票张数 ×3

生：姐姐的邮票张数 + 弟弟的邮票张数 = 180

生：画线段图。

3. 引导学生根据两个信息，在师生互动、生生互动中分析数量关系。

师：有什么问题想问问他们吗？

生：姐姐的邮票张数 = 弟弟的邮票张数 ×3，这个等量关系是根据那条数学信息找到的？

生：姐姐的邮票张数是弟弟的 3 倍。

师：还有要提问的吗？

生：・・・・・・

教师指导：对学生不同的表示方式，及时给予肯定和鼓励。在交流的基础上，根据实际情况对找出题目中的等量关系进行指导。为后面列方程解决问题做好准备。

【设计意图：寻找实际问题中数量的相等关系。启发学生从多角度分析数量中的相等关系，明确题目中有两个未知数，为列方程解决问题做铺垫渗透学生的符号意识。】

（三）列方程解决问题。

师：我们用文字、用画图的方式表示了他们相等的关系。接下来，我们该干什么？

1. 鼓励学生自己列出方程，并全班交流说清所列方程中两个未知数的含义及数量关系。

师：在这个问题中，既要求弟弟的邮票张数，又要求姐姐的邮票张数，我们该怎么设未知数呢？

生：我觉得应该设弟弟有 X 张邮票。

生：我觉得应该设姐姐有 X 张邮票。

师：如果设弟弟有 X 张邮票，那么姐姐的邮票张数怎么表示？

生：3x，因为姐姐的邮票张数是弟弟的 3 倍。

师：如果设姐姐有 X 张邮票，那么弟弟的邮票张数怎么表示？

生：1/3x，因为姐姐的邮票张数是弟弟的 3 倍，如果姐姐的邮票是 3 份，那么弟弟的邮票就是其中的 1 份，所以用 1/3x 表示。

2. 尝试让学生独立解方程并检验。

师：那请大家独立尝试列方程并解方程，在练习本上写清。

师：谁想把列的方程到黑白上展示？

生：解：设弟弟有 X 张邮票，那么姐姐有 3X 张邮票。

X+3X=180

4X=180

X=45

3X=45×3=135

生：解：设姐姐有 X 张邮票，那么弟弟有 1/3X 张邮票。

X+1/3X=180

4/3X=180

X=135

1/3X=135÷3=45

师：对于这两种方法，你们有什么想说的吗？

生：我觉得设弟弟为 X 比较好，解起来比较方便。

师：是的，我们一般设 1 份量为 X。

3. 写清答语，反思列方程解决问题的过程。

师：我们解的对吗？

生：对。

师：你是怎么判断的？

生： 我是把求出来的数又代回去了，用 135+45=180，所以我判断是对的。

生：我是用 180 - 弟弟的张数，也就是 180-45=135。

师：通过检验，我们知道了，我们解对了。我们还差点什么？

生：答题。

师：谁去黑板那把答题补上。

教师指导 1：在列方程的过程中，进行指导，因为是两个未知数先设一个未知数为 x，在根据两个未知数之间的数量关系表示出另一个未知数，培养学生反思，检查等良好的决绝问题的习惯。

教师指导 2：对方程的书写格式进行指导。

【设计意图：首先，学生在运用含有未知数 X 表示出姐姐和弟弟的数量关系的基础上，再鼓励学生自主列方程，这是学生接受和理解符号的具体表现，更是学生从数学语言的表达向用符号语言表达的过渡；其次，引导学生独立解方程，在解方程的过程中，学生初步感悟了用符号表达对解决问题的优势和便捷；同时，用留白的方式让学生自己写出答语，加强学生的反思意识，让学生经历列方程解决问题全过程，发展学生的符号意识。】

（四）巩固拓展  应用方程

师：下面老师把题目改动一下 (展示课件), 你发现什么变了？（姐姐和弟弟一共有 180 张邮票” 改为 “姐姐比弟弟多 90 张邮票）可以怎样列方程解答呢？

1. 引导学生观察把情境中的信息改过来，并尝试分析题意，找出等量关系。

师：请大家独立思考，然后在练习本上 写清 。

2. 全班进行交流。

师：谁想跟大家交流自己的想法？

生：解：设弟弟有 X 张邮票，那么姐姐有 3X 张邮票。

3X-X=90

2X=90

X=45

3X=3×45=135

答：弟弟有 45 张邮票，姐姐有 135 张邮票。

3. 梳理列方程解决问题需要的关注问题。

小结：刚才我们用了方程法解答了含两个未知量的问题，那么用方程法来解两个未知量的实际应用问题应怎么做呢？要先找等量关系，合理设置未知数并表示出另一个量，通过等量关系式列方程，解方程并求出另一个量，最后验算并写答。

(板书：找、设、列、解、验、答)

教师指导：教师巡视指导，遇到学习有困难的学生引导学生仿照前面的问题进行解答。

【设计意图：变换题目中的信息，提出新的用方程解决的问题，学生通过找、设、列、解、验、答的学习过程，经历了从感受到理解，再从理解到应用，一步步的帮助学生体悟了符号意识的形成过程，

在知识迁移的过程中，加深了学生对符号的理解和感悟。】

三、实践提升

师：在前面的学习中，同学们发挥集体的智慧共同解决了数学问题。下面需要你们独立完成学习任务啦，请同学们把书翻到 70 页完成第一题。

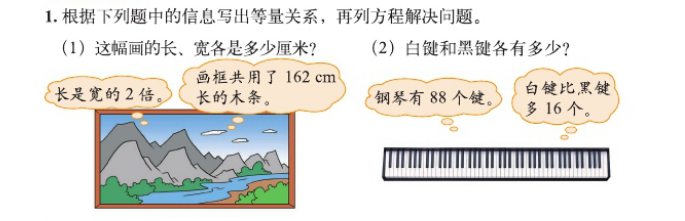
【设计意图：学生再次经历解决问题的过程，先读懂题意，根据信息找出等量关系，再根据等量关系列出方程求解。帮助学生从不同的情境中体会方程的含义。介绍数学家韦达目的是激发学生的创新意识和符号意识。】

四、回顾学习过程，分享收获

1. 请你回顾本节课，我们是如何学习本节课的？

2. 这节课你有哪些收获和困惑呢？

板书设计：