教学三稿：

探索日历中的规律

【教学内容】

新世纪小学数学六年级下册第 88 页总复习《探索规律》巩固与应用的第 5 题，化小为大，丰富拓展为一节探索活动课。

【教材分析】

“日历” 生活中随处可见，学生非常熟悉。日期数之间存在着各种关系、规律，探索发现日历中数的规律，并学习用字母及含有字母的式子表示这些规律，是解决真实情境中存在的真实数学问题，有利于激发学生学习兴趣，使学生体会数学与生活密切相连，有利于激发学生用数学的眼光来观察世界。

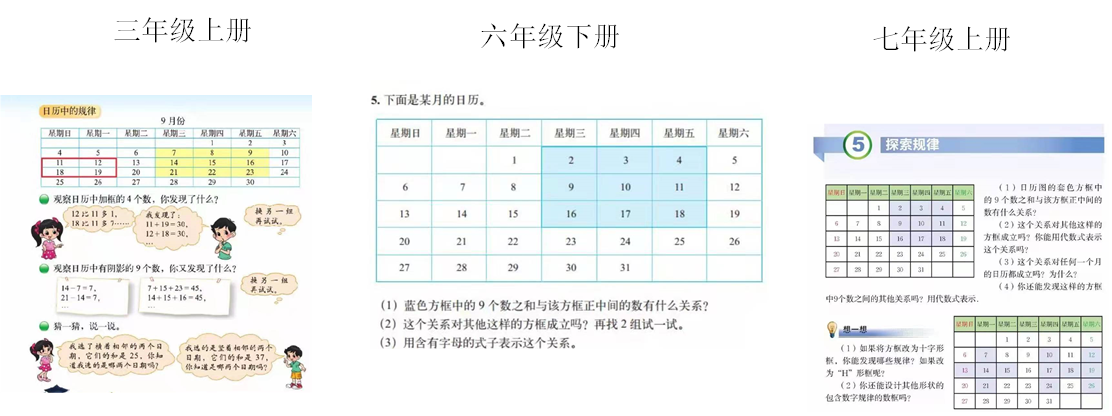
《探索日历中的规律》贯穿小学、初中。三年级上册 “数学好玩” 中学生初步探索了日历中的规律，但只是简单的去观察、发现日历中的规律，并没有抽象成符号；六年级下册第 88 页总复习《探索规律》巩固与应用的第 5 题是一道 “探索日历中的规律并用字母表示规律的题目”。但是教材中只呈现了一个题目，内容少且深，学生原认知与现在学习之间跨度大，有断层，理解掌握起来困难大；七年级上册第三章整式及其加减中的第 5 小节《探索规律》也有这一内容，对我区初中教研员进行了访谈，了解到七年级学生学习这个内容仍然困难很大。

【学生分析】

六年级学生拥有了一定用字母表示数的知识与经验，结合具体情境，会用字母表示比较简单的数和数量关系，能用字母表示运算律和有关图形的计算公式。具有一定的抽象概括能力、语言表达能力和自主合作探究等学习能力。但是这些认知基础与经验都是简单的、初步的，他们还没有建立起运用符号语言表达思想的意识。因此，用字母来表示所发现的规律对于学生来说是本节课学习的难点。

【我的思考】

我的思考：如何化解现在学生学习困难？如何为初中的进一步学习打好基础？

1. 丰富内容，减缓坡度。 先充分探索、分析九个日期数之间的数量关系及规律，并用字母及含有字母的式子表示；学生有了知识基础、探究经验，再解决教材中方框中九个数之和与中间数之间关系的问题。循序渐进，化解难度。

2. 明确目标，做好衔接。

六年级主要目标：探索、分析、用字母或含有字母的式子表达数量关系及规律

七年级主要目标；用字母表示并借助运算将具体规律推广到一般。

目标不同，螺旋上升，小学学习为初中进一步学习打好基础。

【学习目标】

1. 探索、分析日历中数的数量关系及规律，并会用字母或含有字母的式子表达这些数量关系及规律，初步培养学生运用知识与经验解决问题的能力。

2. 经历探索、分析、用字母表达日历中的数量关系及规律的过程，体验从特殊到一般探究规律的方法，开放思维，培养抽象能力，发展符号意识。

3. 感受数学与生活的密切联系，培养学生合作交流的能力，体验学习数学的乐趣，发展学生合情推理的能力。

【教学过程】

一、情境激趣

出示日历：同学们，你们喜欢看魔术吗？老师会变魔术，想不想看看。随意拿出一张日历，不管你们盖住日历的哪一个九宫格，老师都能迅速求出九宫格中九个数字之和，你们相信吗？不信我们可以试一试。

师生活动：教师请一名学生到讲台上随便盖住日历中的一个九宫格，老师迅速的回答出九宫格的数字之和。

教师小结：日历的日期数中还存在着很多的奥秘，这节课我们一起来探究。

【设计意图】在本次活动中，改变以往教师考学生的惯例，由学生来考老师，更能体现师生间的平等地位，拉近师生间的距离，使师生可以更好地互动，同时教师能迅速回答九数之和，也能激发学生的好奇心，求知欲。

二、探究新知

1. 自主探究

根据要求完成问题。

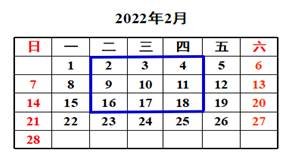
（1）观察：蓝色方框中的数之间有什么规律？

（2）这个规律对其他这样的方框成立吗？再圈几组试试。

（3）用含有字母的式子表示你发现的规律。

【设计意图】给学生充分的时间与空间，在已有知识与经验的基础上，自主探索蓝色方框中的数之间的规律，尝试用字母或含有字母的式子表达数量关系及规律。

2. 开放交流

组织学生针对自主探究中可能出现的几种典型情况交流、研讨。

问题 1：你同意哪个？为什么？

经过比较、讨论，发现：第一种方法中的 a、b、c 只能表示三个任意数；第二种方法既能表示数量，又能表示数量之间的关系。例如 “a+1” 可以表示这一行的第二个数，还可以表示第二个数比第一个数多 1。学生初步感受字母表示数的意义。

问题 2：你同意哪个？为什么？

在上面讨论的基础上，进一步比较、讨论，发现：第一种方法只关注了横行之间的关系；第二种方法只关注了竖列之间的关系；第三种方法既关注了横行之间的关系，也竖列之间的关系。学生对字母表示数有了较为深刻地认识。

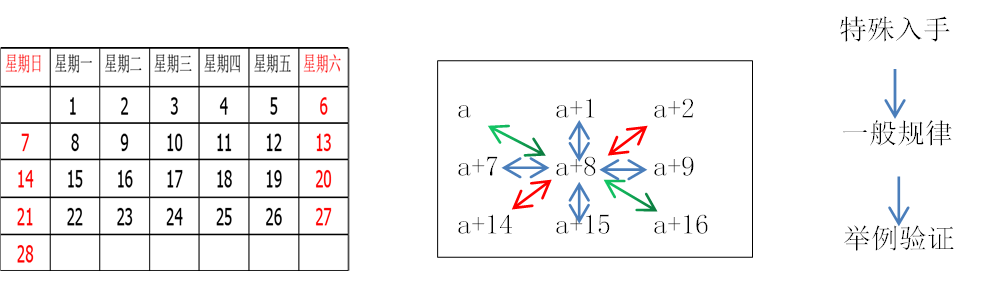
问题 3：“a+8” 表示什么意思？

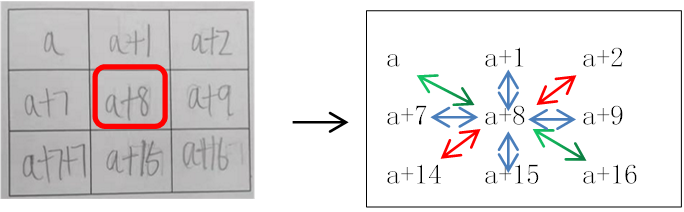
“a+8” 表示的意思是开放的，不止是横、竖，还有左斜和右斜，可以从八个方向理解。开放性的问题，有利于学生更深刻的理解字母表示书的意义，而且非常有利于培养学生思维的灵活性、全面性、深刻性。

3. 举一反三

问题 4：还可以设哪个数为 a？任选一个数设为 a，另 8 个数如何表示？

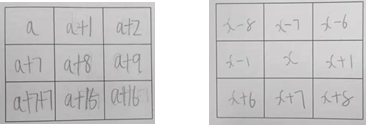
应用中开放思维，深刻的理解、掌握、应用用字母表示数及数量关系。

4. 类比迁移

问题 5：哪里有类似的规律？（圈出九个数，找规律，用字母表示。）

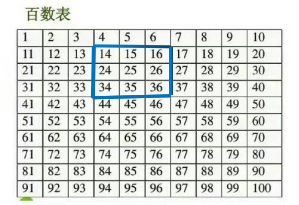
【设计意图】每个环节都给学生留足充分的时间与空间，让学生自主去探索，放开去交流，大胆去尝试。从只关注用字母表示数量，到既关注用字母表示数量，又关注表示数量之间的关系；从只关注横看或竖看，到既关注横行之间的关系，也关注竖列之间的关系；再到举一反三，类比迁移。环环紧扣，螺旋上升，逐步清晰、深刻学生对字母表示数的认识与理解。

三、解决问题

（一）解决问题

1. 根据要求完成问题。

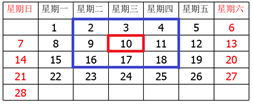
（1）蓝色方块中的九个数之和与该方框正中间的数有什么关系？

（2）这个关系对其他这样的方框成立吗？再找 2 组试一试。

（3）用含有字母的式子表达这一关系。

2. 自主探索。

3. 汇报交流。

预设：

方法 1 例举求和 2+3+4+9+10+11+16+17+18=90 90÷10=9

方法 2 字母表示数

a+1+a-1+a+7+a-7+a+6+a-6+a+8+a-8+a=9a

（二）类比迁移

探索七个数、五个数之和与中间数之间的关系并用字母表示。

（三）解释应用 应用前面知识与经验揭秘课前魔术的秘密。

【设计意图】运用前面学习中已有的知识和积累的经验，解决日历中的数学问题，解释本堂课最开始的小魔术，有利于激发学生学习数学的兴趣，提高学生利用所学知识解决问题的能力。

四、回顾总结

通过本节课的学习有什么收获？

板书设计：探究日历中的规律