二稿教学设计反思：

针对一稿中的问题，我们团队进行了几次认真的研讨、调整、试讲。实践出真知，通过试讲对本节课有了更为深刻的认识，更为成熟的想法。

一、成功之处

（一）教学背景分析，使教学目标更明确

《探索日历中的规律》贯穿小学、初中。三年级上册 “数学好玩” 中学生初步探索了日历中的规律，但只是简单的去观察、发现日历中的规律，并没有抽象成符号；六、七年级同样有这个内容，但是各有侧重。六年级教学目标是探索、分析、用字母或含有字母的式子表达数量关系及规律；七年级目标是用字母表示并借助运算将具体规律推广到一般。目标不同，螺旋上升，小学学习为初中进一步学习打好基础。

（二）游戏情景引入，激发了学生的兴趣

请一名学生到讲台上随便盖住日历中的一个九宫格，我迅速的回答出九宫格的数字之和。在本次活动中，改变以往教师考学生的惯例，由学生来考老师，更能体现师生间的平等地位，拉近师生间的距离，使师生可以更好地互动，同时教师能迅速回答九数之和，没想到熟悉的日历中，竟然存在着这样的奥秘，极大地激发了学生的求知欲。

（三）教学过程开放，利于发展学生思维

本节课每个环节都给学生留足充分的时间与空间，让学生自主去探索，放开去交流，大胆去尝试。教学环节环环紧扣，螺旋上升，逐步清晰、深刻学生对字母表示数的认识与理解。

1. 自主探究

游戏激发了学生的探究愿望，教学顺势而为，给学生充分的时间与空间，让学生自主探究方框中 9 个数之间的关系。

2. 开放交流

自主探究的过程中，巡视时发现了学生的用字母表示的几种典型情况。

组织学生交流研讨：

问题 1：你同意哪个？为什么？

经过比较、讨论，发现：第一种方法中的 a、b、c 只能表示三个任意数；第二种方法既能表示数量，又能表示数量之间的关系。例如 “a+1” 可以表示这一行的第二个数，还可以表示第二个数比第一个数多 1。学生初步感受字母表示数的意义。

问题 2：你同意哪个？为什么？

在上面讨论的基础上，进一步比较、讨论，发现：第一种方法只关注了横行之间的关系；第二种方法只关注了竖列之间的关系；第三种方法既关注了横行之间的关系，也竖列之间的关系。学生对字母表示数有了较为深刻地认识。

问题 3：“a+8” 表示什么意思？

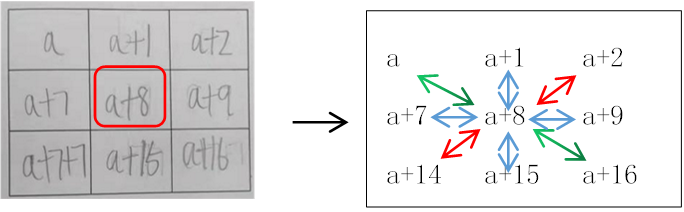
“a+8” 表示的意思是开放的，不止是横、竖，还有左斜和右斜，可以从八个方向理解。开放性的问题，有利于学生更深刻的理解字母表示书的意义，而且非常有利于培养学生思维的灵活性、全面性、深刻性。

3. 举一反三：

问题 4：还可以设哪个数为 a？任选一个数设为 a，另 8 个数如何表示？

应用中开放思维，深刻的理解、掌握、应用用字母表示数及数量关系。

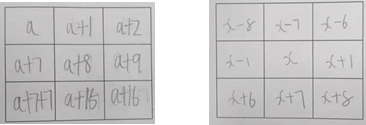
二、问题及改进 通过试讲，发现本节课比迁移不足，训练略显单薄。

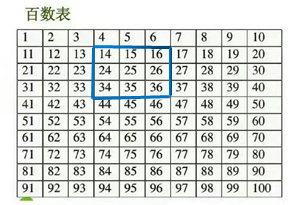
（一）探究新知识后的类比迁移不足 探求新知识后，缺乏类比迁移的过程，我们团队进行了认真的研讨，发现百数表中也有类似的规律，可以让学生圈出九个数，去找规律，去用字母表示，类比迁移可以丰厚学生对用字母表示数的理解。

（二）解决问题后的训练略显单薄 解决问题处略显单薄，解决了九个数之和与中间数的问题，还可以类比迁移到七个数、五个数与中间数之间的关系，并用字母表示。

反思是为了更好地促进教学，接下来我们将继续完善教学设计，开展课堂教学研究。