教学目标

1、经历直观操作、探索的过程，体验发现摆三角形的规律的方法。

2、在小组合作和同伴交流中找到三角形的个数与根数之间的关系，并能用符号进行概括。

3、体会符号概括的便捷性和概括性，发展符号代数思维的意识。

4、能在找规律的情境中解决问题时，想到先用符号进行概括，在解决具体问题。

教学重点

在小组合作和同伴交流中找到三角形的个数与根数之间的关系，并能用符号进行概括。

教学难点

体会符号概括的便捷性和概括性，发展符号代数思维的意识。

教学过程

一、操作引入，揭示课题

讨论摆的方式

师：这节课我们来研究图形中的数学问题。

出示问题：摆 33 个三角形，需要多少根小棒？

（请生 1 上来摆）师：你是每摆 1 个，就需要用三根小棒，这样独立分开摆的。

（请生 2 上来摆）师：这种摆法有什么特别的地方？

师：观察的很仔细，我们把这样的边称为 “公共边”，如果按照这种方式摆下去，会用到多少根小棒呢？（需要 99 根那么多吗）

师小结：看来摆的方式不一样，会引来结果的不同，我们要先确定摆的方式，再得出结果。

设计意图：体会三角形摆法的不同，所用小棒根数就不同。

二、化繁为简，探索规律

（一）明确探究方法

师：按照第一种摆法，摆 33 个三角形需要 99 根小棒，用 33×3 就可以解决。按照第二种方式摆 33 个三角形需要几根小棒呢？说说看，你们打算怎样解决这个问题。

师：很有想法，天下难事必作于易，我们可以由易到难去分析问题。下面请同学们探究一下，这种摆法有什么规律。

（二）合作探究规律

师：拿出学习单，我们一边摆一边从 1 个三角形需要几根小棒探究起。

1、动手操作，初探规律。

（1） 出示活动要求。

①用画一画或摆一摆的方法，完成表格。

②把你的想法用算式表示出来。

（2） 分享汇报，发现规律。

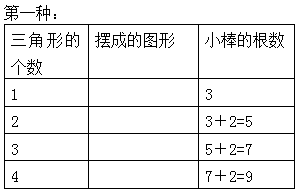
师：你是每次在上一次的基础上进行累加。

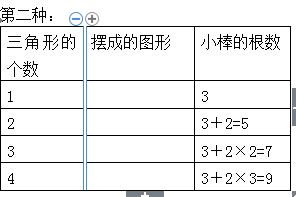
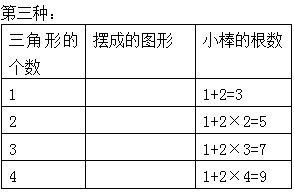
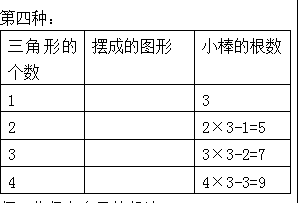
（3） 运用规律，找到三角形的个数与小棒根数之间的关系。

师：按照你们所想的解决办法，摆 5 个三角形需要几根小棒？

师：摆 10 个三角形需要几根小棒？

师：想要快速解决这个问题，看来必须要找到三角形的个数与小棒根数之间的关系。而这三种方法都蕴含了两者之间的关系，因此我们能够快速解决。

（4） 运用规律，解决问题

师：现在你们能够解决摆 33 个三角形需要多少根小棒的问题了吗？

小结：看来找到了两者之间的关系后，我们不需要去摆或者画，就能算出数量。

设计意图： 感受算式累加的方法在计算更多项时不够方便，也不易表达，从而体会只有找到三角形的个数与根式之间的关系，才能更好帮助我们解决问题

三、编写信息，情境性概括

师：现在，请你们给同伴写一段文字，或者配上图，告诉他如何快速计算出摆几个三角形所需要的小棒数量。

设计意图：将注意力转移到关注变量及其关系上

四、符号代数思维的产生

（一）符号公式

1、师：现在，我不想让你们用语言来表达，我想让你们写一个计算公式，有什么建议吗？（注意三角形的个数是未知的）

2、我写一个公式，看你们是否能够解释字母的意义。

或：用 n 来表示三角形的个数，试着表示一下你们小组发现的关系，并解释每一步的意思。

3、对比一下，你更喜欢哪种方式来表示这种关系，为什么？

4、对于这个公式，你有什么想说的？

（引导学生发现这个公式包括了所有的算式）

设计意图：培养符号化意识，符号的概括，不仅在于字符体系的引入，还在于对数字运算的重新认识。

五、拓展练习

蜜蜂的蜂窝构造非常精巧、适用而且节省材料。蜂房由无数个大小相同的房孔组成，房孔都是正六角形，每个房孔都被其它房孔包围，两个房孔之间只隔着一堵蜡制的墙。这种蜂窝结构强度很高，重量又很轻，还有益于隔音和隔热。因此，现在的航天飞机、人造卫星、宇宙飞船在内部大量采用蜂窝结构，卫星的外壳也几乎全部是蜂窝结构。因此，这些航天器又统称为 “蜂窝式航天器”。

（1）师：我们看到蜂窝的蜂孔排列整齐，而且很有规律，下面是老师截取的其中一列，你们能研究一下这个图形有什么规律吗？并请你们用一个公式表示出来。

（2）照这样的规律排列下去，请你算一算摆 60 个正六边形时，有多少条边？

设计意图： 体会到符号赋予了学生数学问题解决的力量