教案一稿：

教学内容： 北师大版小学数学三年级下册《长方形的面积》。

教材分析： 从课标定位和教材设计意图来看，我们在探究长方形面积有多大时，要引领学生认识到长方形的面积本质是看长方形中含有多少个面积单位。用面积单位直接度量是一种比较直观的方法，但是这种方法比较麻烦，逼着学生再通过思考、操作、推导出长方形面积的计算公式。在整个探究活动中，学生的分析、推理、抽象概括的能力得到提升，长、宽、面积公式等符号化的意识得到发展。

学情分析： 有些学生已经知道了长方形面积的计算方法，但并不一定真正理解长 × 宽计算的道理，很少有学生主动想到和面积单位的个数对应，学生的空间观念还需要继续培养。学生只有经历完整的知识形成过程，才会对面积公式有理性的认识，对面积公式的抽象概括有个符号化的认识过程。

学习目标：

1. 经历探索长方形和正方形面积公式的过程，掌握长方形、正方形面积计算的方法，能够解决相关的实际问题。

2. 在面积公式的推导过程中，学生的分析、推理、抽象概括的能力得到提升，符号化的意识得到发展。

3. 能利用长方形面积公式推导的经验，迁移到其他图形面积的探究。初步养成独立思考，勇于探索的习惯。

重点： 经历探索长方形和正方形面积公式和符号化的发展过程，掌握长方形、正方形面积计算的方法。

难点： 理解长方形面积公式的算理，灵活应用长方形面积解决实际问题。

教学准备：

多媒体课件，直尺，面积单位的正方形模型、学习单。

教学过程：

一、 导入新课。

师：同学们，看到它（出示两张长方形纸片），你想到了什么？这两个长方形，哪个大？比较它们的大小实际是比较什么？你觉得长方形的面积和什么有关？

生猜想。

【设计意图：开门见山，让学生在比较两个长方形大小中，明白长方形的大小就是长方形的面积，为进一步认识面积，探究面积公式做好铺垫。】

二、 探究新知。

（一）自主比较

师：怎样比较这两个长方形的面积？说说你的方法。回想前面我们学习了什么？借助 1 平方厘米的小正方形来估一估这个长方形的面积？

生估计。

师：怎样知道它到底有多大？引导学生用 1 平方厘米的小正方形进行测量。

（二）活动操作

1. 摆一摆，数一数。

2. 反馈交流。

（1）铺满

一共摆 6 个小正方形，所以它的面积是 6 平方厘米。

（2）铺部分

一行摆 3 个，第二行摆 1 个，可以推想能摆 6 个。

3. 对比小结

师：摆满的和没有摆满的，都可以通过数面积单位，知道面积是 6 平方厘米。

4. 不规则摆放

观察以上两种摆法，还能拿走几个，保证能看出一行几个和行数。

预测：

5. 推理想象

（1）有标记

现在老师将面积单位都拿走，留下了标记。你能看出这个长方形的面积是多少吗？

每行摆 3 个，就是沿着长摆了 3 个边长是 1 厘米的正方形，摆了 2 行。引出长是 3 厘米，宽是 2 厘米，面积是 6 平方厘米。

（2）无标记

师：怎么知道这个长方形的面积呢？

引导学生测量出长和宽。

6. 归纳小结

(1) 公式归纳   

    根据对应关系，归纳出长方形的面积 = 长 × 宽

（2）字母式         

S=a×b

小结：长就是每行面积单位的个数，宽就是有这样的几行，长方形的面积其实就是面积单位的总个数。计算长方形的面积也就是计算面积单位的总个数。

【设计意图：通过多种形式的操作，让学生明白长方形的面积是看长方形中有多少个面积单位，从铺满 -- 铺部分 -- 推理想象 -- 归纳公式，在逐步抽象中渗透长、宽和面积公式的符号化发展意识】

三、巩固练习

1. 口算面积

它们的面积是多少（逐个出示）？

（1）交流汇报

你是怎么看出它们的面积的？

（2）对比发现

发现正方形的面积计算公式。

2. 笔算面积

如果上面的图形上铺草皮，做花坛，你能算出它们的面积吗？（单位：米）

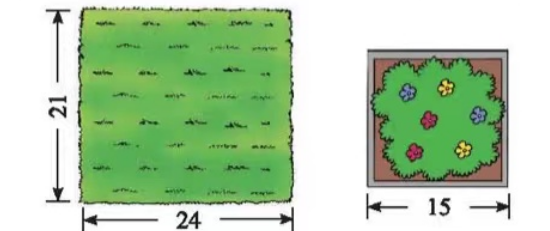
【设计意图：在口算面积中让学生计算正方形的面积，学生在体会到正方形是特殊长方形的同时，还能体会到用长 × 宽计算面积，这种符号化的表达具有一般性。学生迁移的学习能力在知识、技能等方面潜移默化中得到提升。】

四、拓展提升

1. 看数据，想图形

出示 300 平方厘米，你能想到什么图形？

引导：面积相同的长方形，形状可能不一样。

2. 长方形变形记

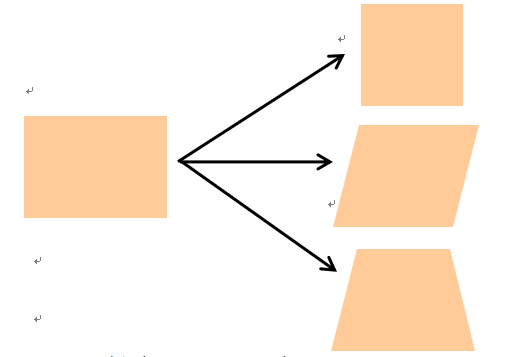
（1）长方形 —— 正方形

回顾面积推导过程，积累面积探究经验。

（2）长方形 —— 平行四边形

面积探究经验的迁移。

（3）长方形 —— 其他图形

推想探究方法

【设计意图：给学生知识，不如给学生知识结构，长方形的面积公式的正向利用，每个孩子都会。看数据想图形，不仅体现了公式的逆向推导，还渗透了数形结合的思想，让学生在应用公式的基础上又提升了学生思维。长方形面积公式是其他图形面积公式推导的根基，在图形变形记中，让长方形面积探究经验迁移到其他图形面积探究之中，从而凸现符号化意识的重要性。】

五、全课总结

通过学习，你有什么收获？

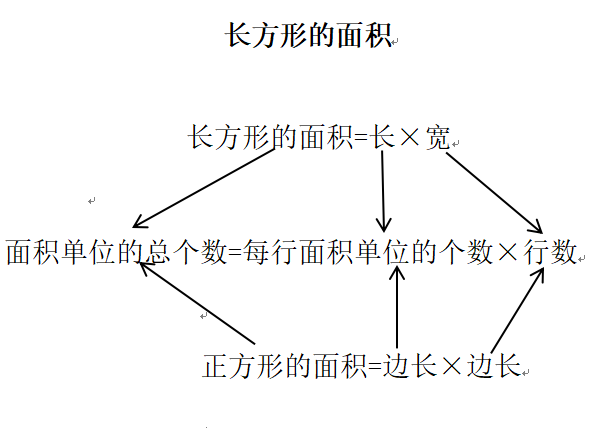
板书设计