北师大版数学五年级上册《图形中的规律》教学设计（第一稿）

湖北省宜昌市伍家岗区实验小学中南校区袁雪雯

教学目标：

1、经历直观操作、探索的过程，体验发现摆三角形的规律的方法。

2、能在观察活动中，发现点阵中隐含的规律，体会图形与数的联系。

3、结合探索、尝试、交流等活动，发展归纳与概括的能力。

教学重点：

找出图形中隐藏的规律，将 “图的规律” 转化成 “数的规律”。

教学难点：

培养分析、推理的能力；渗透符号化思想。

教学过程：

一、活动导入

1、出示 10 根小棒

师：这里有一些小棒，想用它们来摆三角形，可以摆几个呢？

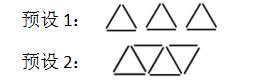
2、第一种摆法可以摆出几个？需要几根呢？按照这样的摆法，如果摆 5 个三角形需要多少根小棒？摆 10 个呢？怎么知道的。

3、也就是说，你们找到了根数与三角形个数之间的关系，可以用你喜欢的方式将这个关系表示出来吗？

小结：用符号表示关系清晰明了，是一种不错的方式。

【设计意图】初步体会用符号表示简单两个量之间的关系及规律的好处，为下面用符号表示关系做铺垫。

二、探究新知

1、第二种摆法是怎样摆的，看懂了吗？谁来说说。

①可以看做是先摆 1 个三角形需要 3 根，后面的三角形每次只需要 2 根。

②也可以看做是把两个三角形拼一起，总根数就会少 1 根，再增加一个三角形，又会少 1 根。

2、你还能找到根数与三角形个数之间的关系吗？在下表中试试看吧。

3、同桌互相交流一下你的发现吧。

4、汇报分享 1：第一个三角形需要 3 根，每增加 1 个三角形需要两根小棒。

5、根据你们的发现，在旁边用算式试着表示一下。

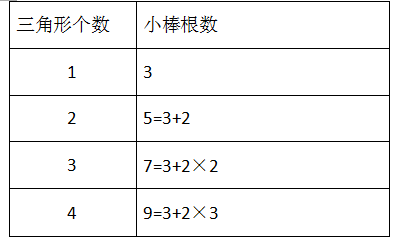
6、10 个三角形需要多少根小棒，能不画图，直接列算式得出结果吗？

3+2×9=21，解释一下这个算式的意思。（重点解释为什么 ×9）

7、按照这种摆法，如果要摆 n 个三角形，需要多少根小棒？试着表示出来。3+2×（n-1）

8、如果我要这样摆 1000 个三角形你们知道需要多少根小棒吗？怎么算的？10000 个呢，能算吗？

小结：看来用符号表示关系，还方便我们进行应用。

汇报分享 2：

刚才还有同学是从另一个角度看待问题的

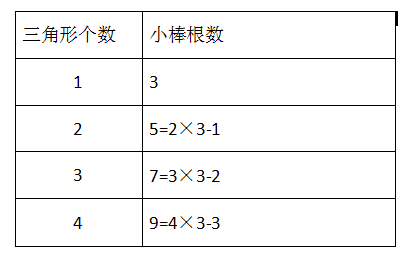
摆 2 个三角形需要的小棒数比 6 少 1......

【设计意图】通过直观操作、探索的过程，体验发现摆三角形的规律的方法，并通过符号化进行表示。

三、巩固拓展

1、想一想，笑笑接着摆下去，一共用了 37 根小棒，你知道她摆了多少个三角形吗？

2、想一想，摆 18 个三角形需要多少根小棒？

【设计意图】在探索了三角形的排列规律后，应用规律来解决问题。同时，也是对规律的验证。

四、点阵规律

过渡，刚才我们利用了符号表示了两个量之间的规律，还方便我们应用，老师这里还有一组图，你能发现他们的规律并用符号来表示规律吗？

1、交流：点阵之间的关系是什么？

2、第 n 个点阵用符号如何表示？

3、换个角度观察点阵，又能发现怎样的规律？

【设计意图】通过探索点阵图的规律让学生感受到解决数学问题的本质是抓住相同的思维模型，感悟它们之间的内在联系。

五、练习设计。

1、按下面的方式摆桌子和椅子，一张桌子可坐 4 人，两张桌子可坐 6 人。

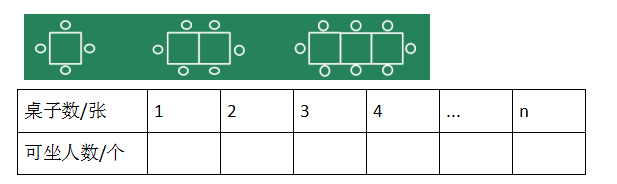
照这样摆下去：

(1) 12 张桌子可坐 (   ) 人。

(2) 坐 80 人需要 (   ) 张桌子。

(3) 把以上表格填完整。

2、看图解决问题。

（1）用算式表示点阵中点的个数。

（2）第 5 个点阵中有 (   ) 个点，请在下面画出这个点阵。

【设计意图】应用规律来解决问题，同时，也是对规律的验证。

六、课堂小结

这节课你学到了什么？

【设计意图】对本堂课的知识进行梳理与回顾、归纳，形成一个完整的知识认知体系，提升学习方法。