《字母表示数》教学设计三稿

《字母表示数》教学设计（三稿）

陕西师范大学附属小学 陈琴琴

一、唤起经验，准备建构

1. 由课前预习单引到英文单词的缩写，即字母表示特定的意义。

2. 数学中的字母缩写也表示特定的意义。

例如： 一个小朋友的身高是 1.3 米，可以写成 1.3m，这里的 m 是 meter 的缩写。

乐乐的体重是 27 千克，可以表示成 ——27kg。

3. 字母表示特定的数。

扑克牌中 J 表示 11，Q 表示 12，K 表示 13，A 表示 1。

今天，我们就一起来研究 “用字母表示数”。

追问：看着这个标题，你有什么疑问吗？

预设 1：为什么要用字母表示数呢？

预设 2：用字母表示数有什么好处呢？

预设 3：字母可以表示怎样的数呢？

预设 4：怎样用字母表示数呢？

……

师：我们就带着这些问题一起来开启今天的学习。

【设计意图：从生活中的字母缩写到数学中的字母缩写再到数学游戏中的字母表示数，层层递进，唤起学生的经验，让学生理解，字母可以表示特定的意义，也可以表示特定的数，为本节课的教学奠定基础。又用问题激趣，让学生带着问题开展今天的学习，做到心中有数。】

二、多元表征，探究新知

（一）出示字母式：a+b=b+a（字母表示任意数）

问：这个式子是什么？（加法交换律）

追问：：什么是加法交换律？（学生回答）

追问：用字母表示加法交换律有什么好处？

预设： 字母表示更简洁。（板书：简洁）

问：加法交换律中 a 和 b 表示的是什么？

追问：为什么不用 “4+6=6+4” 表示加法交换律？（学生回答）

预设 ：这里的字母可以表示任意数。（板书：任意数）

总结：这里的 a 和 b 具有高度的概括性，它可以表示任意的数。

【设计意图：利用学生熟知的加法交换律作为学生认识字母表示数的第一步，让学生充分体会到，字母可以表示任意的数，且字母表示数具有简洁性和概括性。】

（二）收集硬币（字母表示不确定的数，字母式可以表示数量关系，也可以表示数量）

过渡：同学们都有自己的爱好，我的爱好是收集硬币。我会把收集到的硬币放在存钱罐里。

1. 存钱罐 1：一枚一枚放入硬币。

问：一共放入了几枚硬币？（4 枚）

追问：为什么不用其它数字表示？（学生回答）

2. 存钱罐 2：提前放好硬币。

猜一猜：一共有多少枚硬币？（学生自由猜）

追问：现在同学们的答案都不一样，不太确定有多少枚硬币，该怎么表示硬币的枚数呢？

预设： 用字母表示。（a）

师：看来字母可以表示不确定的数。（板书：不确定）

3. 老师一共收集了多少枚硬币？

预设 1： 不知道，未知数 。

预设 2：a+4 枚

问：为什么要用 a+4 枚表示？

追问：a+4 枚是多少枚？（不知道）

追问：a+5 只是一个算式啊，最后的结果呢？

预设： 结果不知道，因为 a 是未知数。

问：想知道 a+5 是多少吗？课件出示：a+5＝a+5，别看这两个算式全一样，表示的意义却完全不一样了，你信吗？

左边出示： 存钱罐 1 + 存钱罐 2＝存钱罐（a+4）

左边的表示加法运算，右边的表示结果。

追问：同学们不太习惯也是正常的。以前遇到计算结果，可都是用一个具体的数来表示的，这里的结果却用一个含有字母的式子来表示呢？为什么呢？

预设：因为这里的 a 是个未知数，不知道是多少。

问：如果告诉你 a 是多少，这个结果能用具体的数表示吗？

总结：其实，为了区分，我们可以把表示结果的用小括号括起来，表示一个整体。（课件出示）

总结：现在看来，含有字母的式子不仅可以表示一种运算，还可以表示 ——

预设： 运算的结果。（板书：运算结果）

【设计意图：利用收集硬币这一情境，激发学生兴趣。让学生知道字母可以表示不确定的数，有时还表示有一定范围的未知数。含有字母的式子不仅可以表示数量，还可以表示数量关系。】

问：你能用学到的知识表示下面问题的结果吗？

课件出示：

（1）一个储蓄罐有 a 元，小明拿走了 10 元，还剩（   ）元。

（2）一个储蓄罐有 a 元，平均分给 6 人，每人分得（   ）元。

（3）一个储蓄罐有 a 元， 2 个这样的储蓄罐里共有（   ）元。

由第（3）题引到介绍 “X” 和 “×” 的故事和简写算式的方法。（视频播放）

课堂练习（课件出示）：

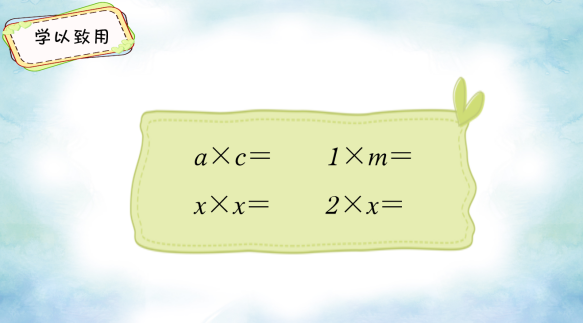
（学生先独立书写结果，然后交流。教师引导学生不仅要说出结果，还要说一说类似的问题需要注意些什么）

【设计意图：介绍字母式的简写规则，为后面的学习奠定基础。】

（三）猜年龄（字母表示具有一定范围的数，字母式不仅表示数量，还表示数量关系）

问：了解了老师的兴趣爱好，你们还对老师的什么感兴趣？

预设 1：身高。

预设 2：年龄。

问：那你们猜猜陈老师有多大了？（学生猜）

问：都说女孩子的年龄是个秘密，不能随便告诉别人，那你们觉得我的年龄应该怎么表示？（用字母表示）

问：同学们已经有经验了，未知的数可以用字母表示。那你想用哪个字母表示？

追问：那我们就用你选的字母 X 来表示吧。刚才，我们知道字母可以表示任意的数，那这里的字母可以表示任意数吗？（学生分享）

追问：看看陈老师，你们觉得我的年龄大概在什么范围？（生互动）

总结：看来，有时候的字母还表示有一定范围的自然数。

问：今天为了上这个课，老师还请来了帮手，这是我的妈妈。（出示妈妈照片）你想怎么表示她的年龄？

学生用字母表示，师生互动。

追问：能用 X 表示吗？（生反驳）

总结：在同一问题中，不同的量最好用不同的字母来表示。不过， 我并不想选择你们提到的任何一个字母来表示她的年龄，而是选择了一种更特别的方式。 怎么样，想不想看看？（课件出示：X+28）

追问：我听到了恍然大悟的声音，你是看懂了什么吗？

预设 1： 我知道您的妈妈比您大 28 岁。

预设 2： 我知道你们两人相差 28 岁。

总结：也就是说，这里的 x+28 不仅可以表示我妈妈的年龄，而且可以表示什么？

预设： 表示你们俩年龄之间相差多少岁。

总结：原来，含有字母的式子既可以表示一个具体的数量， 还可以表示两个量之间的关系。那么，当陈老师 1 岁时，妈妈几岁？ 当陈老师 20 岁时，妈妈几岁？当陈老师 30 岁时，妈妈几岁？

问：观察一下，这里的什么在变，但什么始终没变？

预设： 陈老师和您妈妈的年龄一直在变， 但你们俩年龄之间的相差关系始终不变。您妈妈的年龄始终比你大 28 岁。

问：我还有个帮手，神秘人物，想不想知道他是谁？我可以透露一下他的年龄（X+1）岁。

预设： 他可能是你的哥哥或姐姐。

追问：为什么是哥哥或姐姐，而不是妹妹或者弟弟呢？

预设： 因为他的年龄比你大一岁。

追问：你怎么知道的？（生回答）

总结：看来，（x+1）不仅表示神秘人物的年龄，还表示我俩之间的年龄关系，虽然不能确定他是谁？但能确定什么？（两人之间的年龄关系）。

问：刚才我用 x 来表示我的年龄，如果我用 X 来表示我妈妈的年龄，陈老师和神秘人物的年龄该怎么表示呢？

预设： 陈老师的年龄：（X-28）岁  神秘人物：（X-28+1）岁

预设： 神秘人物的年龄也就是（X-27）岁 。

追问：为什么同一个人，年龄一会儿是（x+1）岁，一会儿是（X-27）岁呀？

总结：当 x 表示的量发生了变化， 表示对应的另一个量的字母式子也就不同了。 这样看来，确定哪个量是 x 重要不重要？（重要）

【设计意图：字母表示有范围的数，并且字母式不仅可以表示数量，还可以表示数量关系。未知数的量不同，数量关系就不同，字母式自然也不同，为后面学习方程奠定基础。】

（四）玩游戏（青蛙儿歌）

过渡：学了这么久，同学们一定累了吧。我们一起歇一歇，动一动吧。我们一起来唱一首儿歌，可以跟着视频一起动动小手。

问：同学们，老师只给出了儿歌的前几句，你能把儿歌继续唱下去吗？……（学生试着续写儿歌，在续写的过程中厘清四种量之间的关系）

追问：能唱完吗？（不能）

追问：那你能用一句话来概括一下这首儿歌的内容吗？（（ ）只青蛙（ ）张嘴，（ ）只眼睛（ ）条腿。）

预设 1：a 只青蛙，a 张嘴，a 只眼睛，a 条腿。

预设 2：a 只青蛙，b 张嘴，c 只眼睛，d 条腿。

预设 3：a 只青蛙，a 张嘴，2a 只眼睛，4a 条腿。

……

问：你认为哪一种表示方式最恰当，请你说明理由。

小组代表发言，并相互辩论。

总结：同学们真厉害，唱不完的儿歌用一个字母式一下子就能概括出来，看来字母式具有概括性。在同一情境中，用字母表示数，不仅要区分不同的量，还要表示出它们之间的数量关系。

追问：同学们，学到这里，你想对用字母表示数说些什么？你课前提出的问题都解决了吗？

生自由发言。

【设计意图：回归教材，让学生充分体会到用字母表示数的必要性和简洁性，并将一种数量关系拓展到多种数量关系，再次强化字母式可以表示数量关系。同时，利用游戏激发学生的学习兴趣。这一环节，充分放手给学生，让学生在相互辩论中厘清数量关系和字母表示数的方法。】

（五）延伸拓展

在生活中，也有很多字母表示数的例子，你能举例说一说吗？

学生自由举例。

三、梳理概括，归纳总结。

师生共同总结知识点，并补充板书。

课外知识延伸。（视频和语音介绍）

【设计意图：通过总结，巩固知识。通过补充板书，画龙点睛，培养学生良好的学习习惯。通过介绍课外知识，让学生感受到课虽尽而意无穷，将课延伸至课外。】