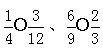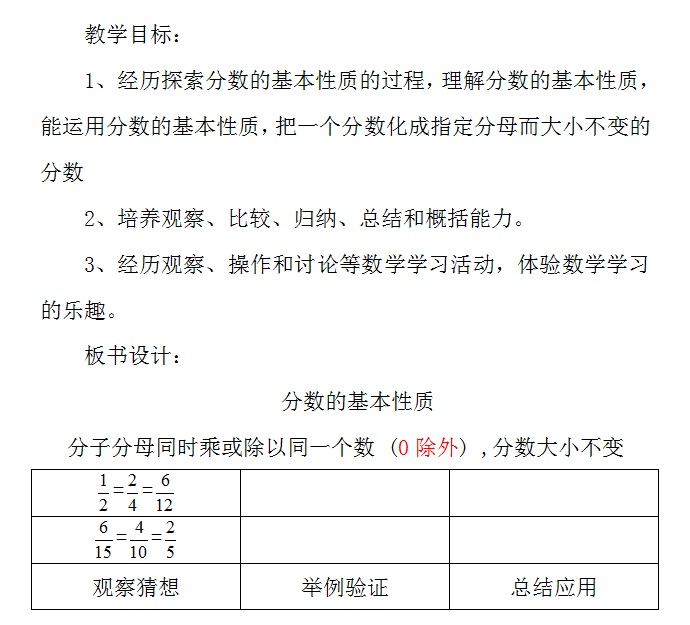
分数的基本性质

（第四稿）

教学过程

课前谈话：

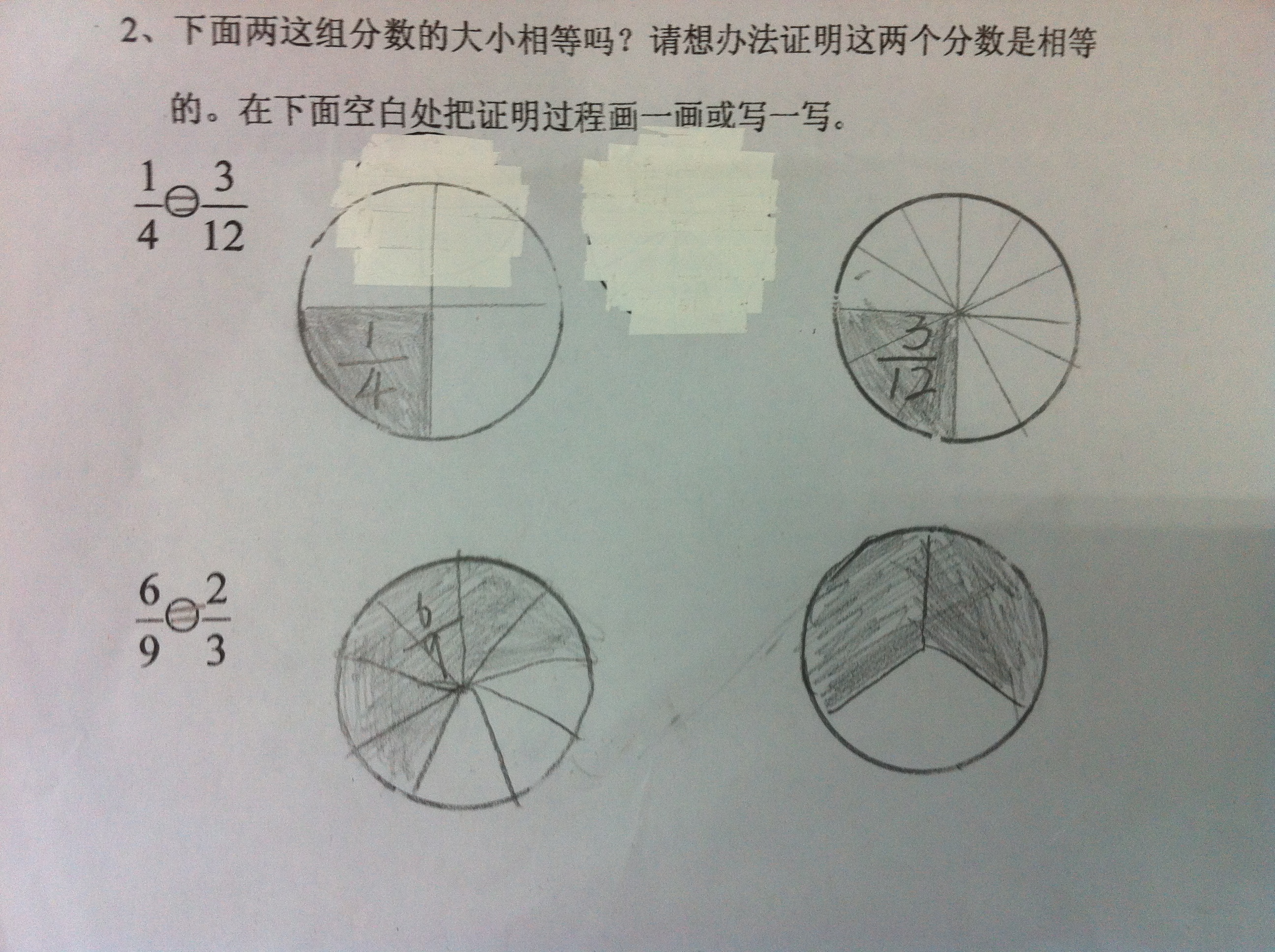
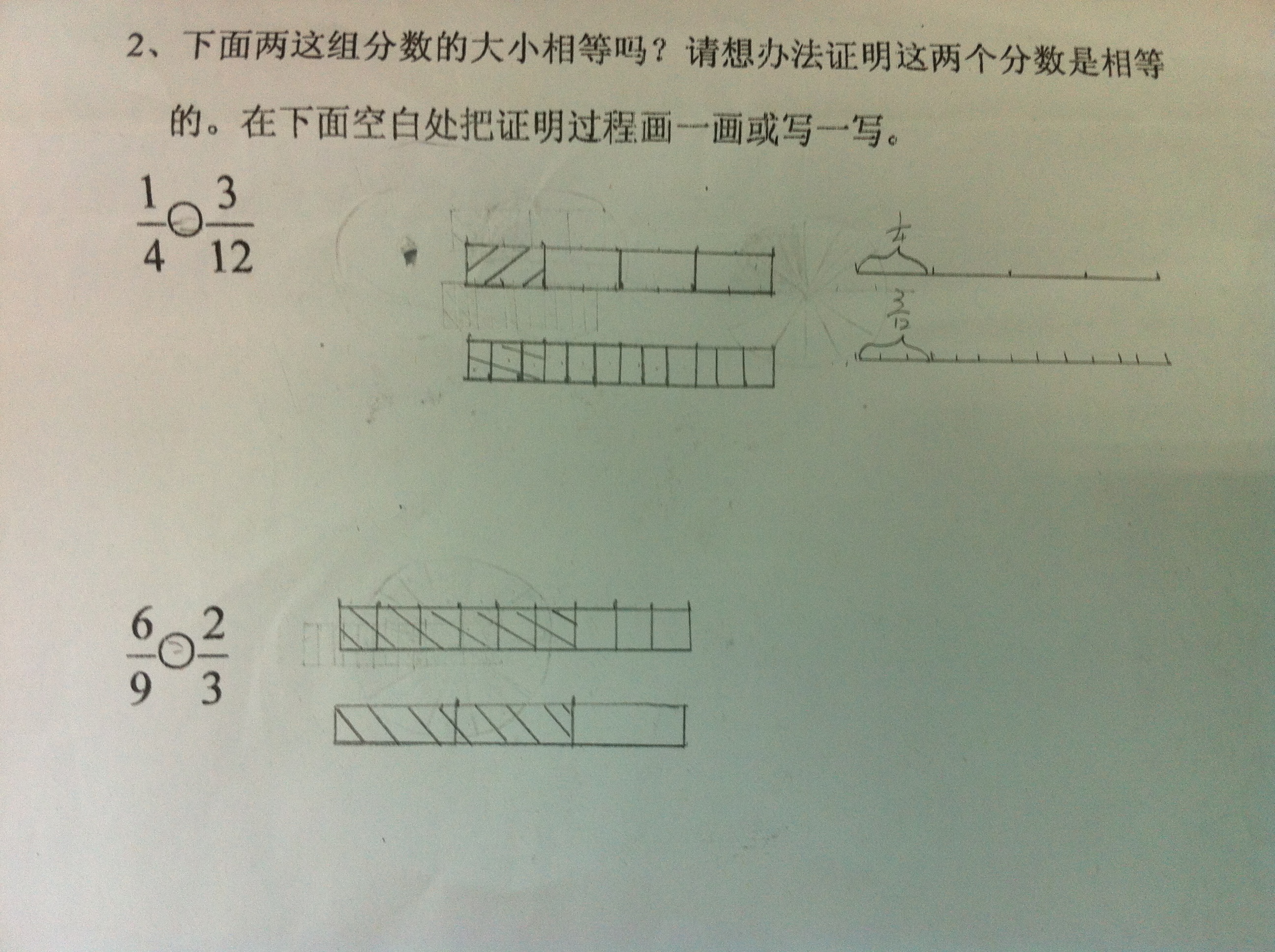
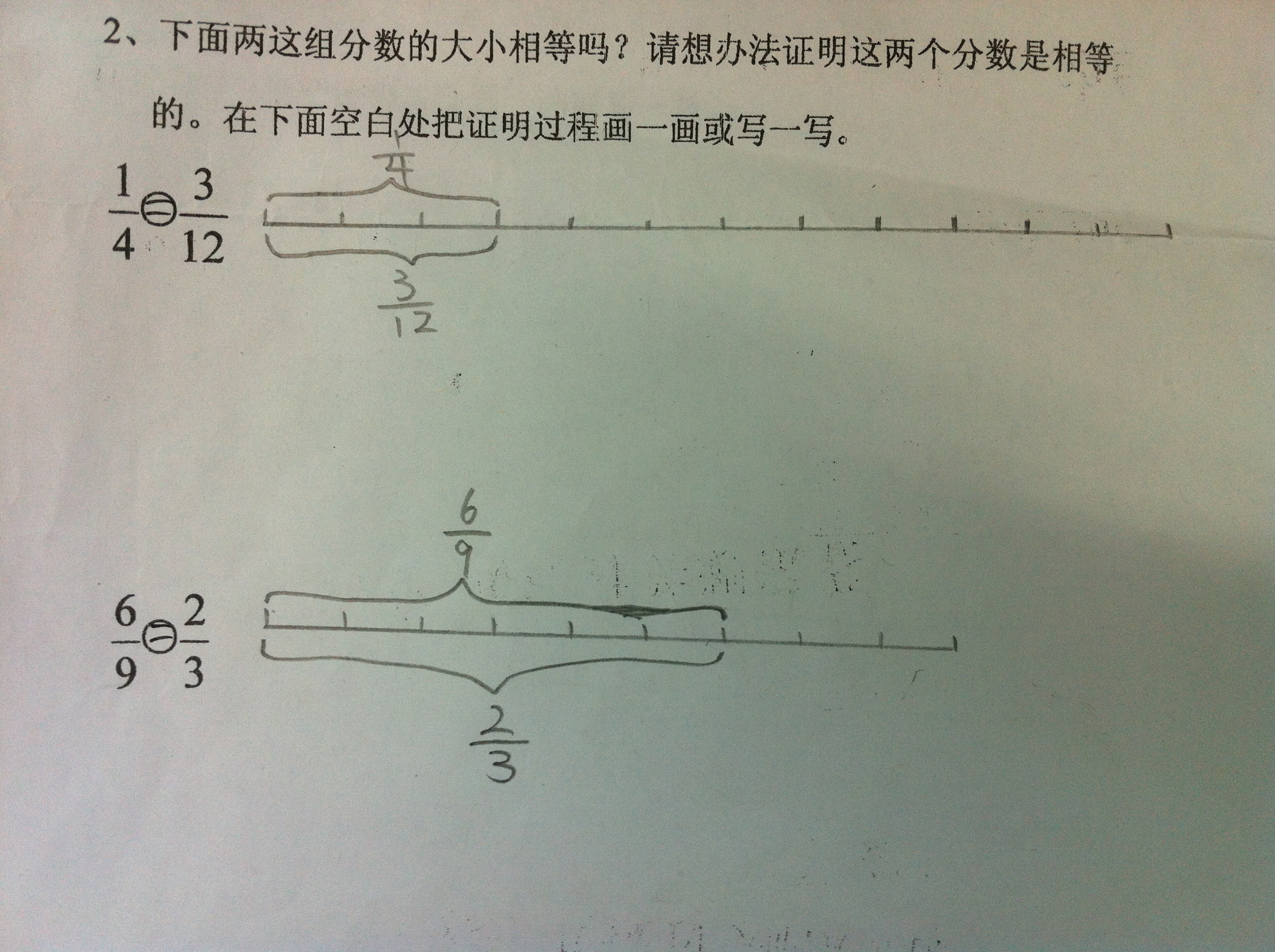
下面的说话对吗？

（1） 教室里除了老师，就是学生。

生：对的，因为教室里除了上课和听课的老师外，就只有我们 503 班的学生了。

师：也就是说教室里找不到第三种身份的人了，所以这句话是对的。

（2） 教室里的老师和学生都是中山小学的。（丽水市莲都区中山小学借班上课）

生：错的。因为张老师就不是中山小学的。

师：很厉害，举一个不是的反例，就能证明这话是错的。看来我们要证明一句话是否正确，最重要的是什么？

生：找到证据证明。

师：是的，数学上经常用举例子来证明一句话的对错，今天我们就要一起来利用这结方法来证明分数中的一些性质。

一、分类观察，猜想规律。

1、 分一分，你能找到哪些分数？

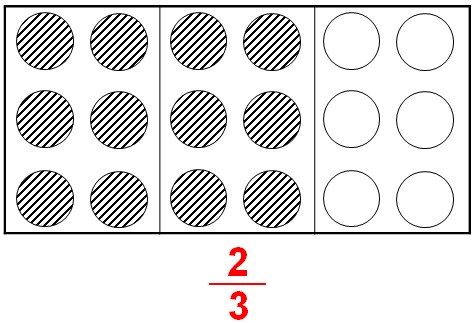
15851586158715881589

师：同样的图，为什么可以用不同的分数表示？这些分数有什么联系？

生 1：整体量是一样的，部分量也是一样的，分的方法不同。

生 2：这些分数的大小都相等，都表示 12 个圆片。

生 3：我发现从 2/3 到 4/6，分子和分母都同时扩大了 2 倍，到 6/9 分子分母同时扩大了 3 倍，到 12/18 分子分母同时扩大了 6 倍。

生 4：我还发现从右往左看，刚好变成了除。

师：谁能把刚才几个同学的发现再说一说？

生 5：……

教后反思：由原来的两组分数分类，变成只研究一组分数的关系，好处在于学生马上集中相等分数的联系，弊端在于分数大小相等的关系学生反而不易发现，而重点放在同时扩大缩小相同的倍数这一关系上，而相等是这一性质的前提，创设怎样的情境既让学生发现相等，又利于研究分子分母之间的相互关系呢？分数大小相等将如何阐述更直观明了？

二、举例验证，总结规律。

师：同学们根据这一组分数发现了一个规律，那 还能找到一些符合规律，大小相等 的分数吗？

生：能（不能）

师：无论能与不能，都是我们提出的一个猜想，要想证明这个猜想是否正确，应该怎么办？

生：举例子，找证据证明。

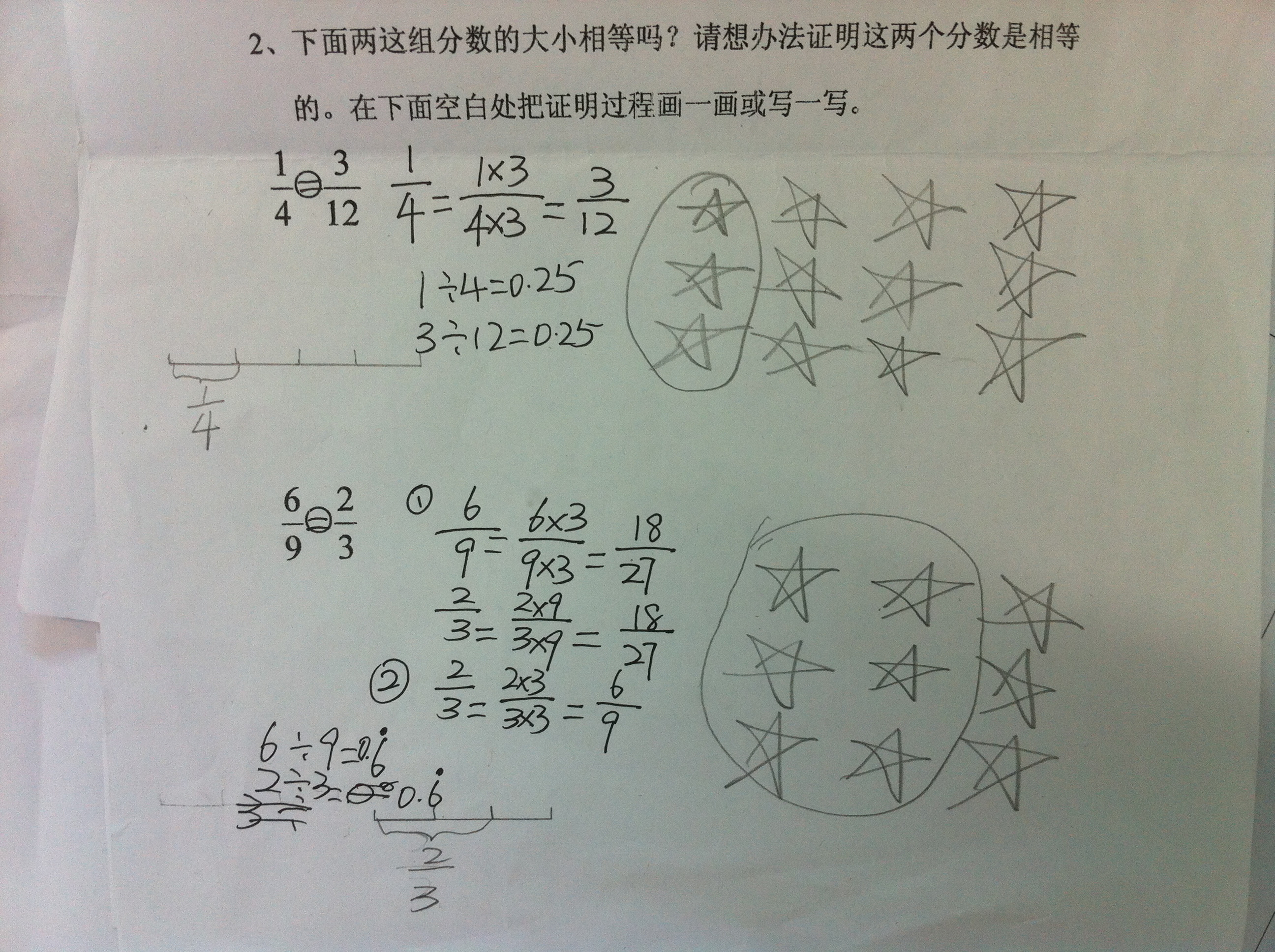
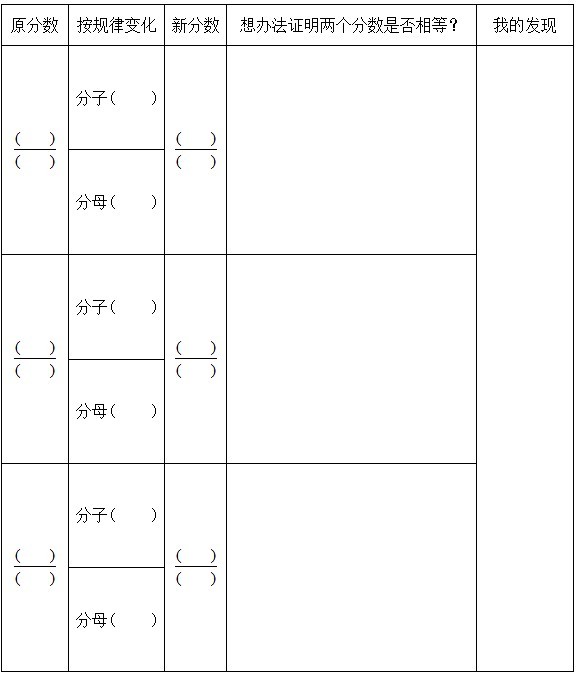
师：好，下面我们就一起来举例验证，老师提供给同学们一些建议：

找相等分数的建议：

1. 在活动纸上折一折，画一画。

2. 根据意义写一写，算一算。

3 . 想一想，说一说你的发现

教师巡视，收集性的分数

课堂反馈，大多数学生采用折一折的方法来证明相等的分数存在以上规律。

学生汇报，师生共同总结：

分子分母同时乘或除以相同的数，分数大小不变。

师：刚才我们是怎样得到这一结论的？

教后反思：由原来的指定分数研究，到放开设定，学生自由折纸，环节相对开放，难度降低。但也有部分孩子直接利用上面的规律来写分数，却并没有说明分数的相等性，陷入循环论证的怪圈。分数的基本性质前提是相等，是相等分数之间存在的变化规律。

四、巩固应用，加深理解

师：下面就要考考大家分数的基本性质学得怎么样了。

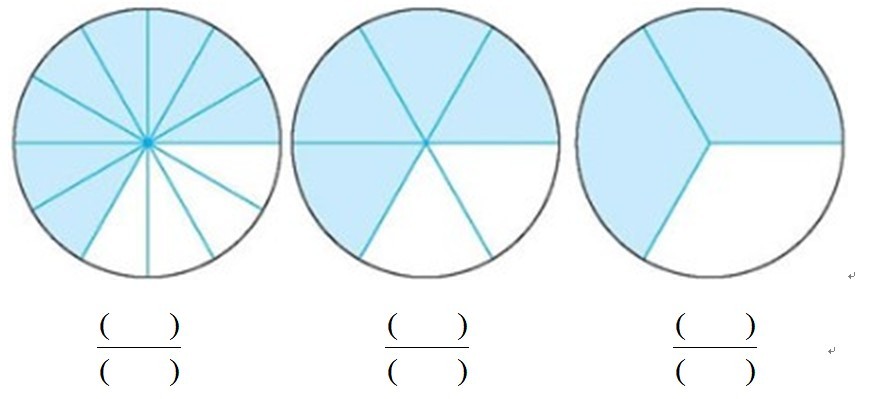
第一层、基础练习：

1590

第二层、分数实际生活背景。

1591

第三层、数学符号化思想。

1592

第四层、变式应用。

1593

第五层、数学学习方法的融会贯通

有人说：“分数的分子、分母都加上或减去相同的数，分数的大小不变。” 你认为这个说法对吗？

设计意图：计算能力是解决问题的基础，培养运算能力有助于学生理解运算的算理，寻求合理简洁的运算途径解决问题。不仅是一种数学的操作能力，更是一种数学的思维能力。在计算的基础上，教师再赋予分数的现实生活意义，既是对计算作用的一种体现，同时让孩子应用分数基本性质的基础上比较在校时间和睡眠时间的长短，初步感知分数基本性质的应用。接着是一组开放题，对 6/8 进行变化，有两层作用，一用字母表示所有的可能性，是符号化思想的体现，二是引出 0 除外，使性质完整。最后对 6/8 的分子进行加减的变化，也有两层作用，一是对分数基本性质的变式应用，分母填上去的数必需符合分数的基本性质，二是有部分孩子会填分子分母同时加或减相同的数，那么等式成立吗？引导学生再次利用举反例的方法来证明定理的不可行性。

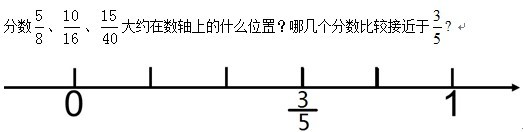
第六层：数感、数学文化的渗透。

1598

1594

1595

1596

1599