《圆的面积（一）》教学设计 终稿

教学内容：

北师大版小学数学六年级上册第一单元《圆的面积（一）》，课本第 14～15 页。

教材分析：

《圆的面积（一）》是新北师大版小学数学六年级上册第一单元的内容。在此之前，学生已经直观认识了圆，学习了长方形、正方形、平行四边形、梯形等平面图形及其周长、面积的计算。它是学生初步研究曲线图形面积的开始，也是后面学习圆柱、圆锥等知识的基础，是小学几何初步知识教学中的一项重要内容。圆的面积的探索安排在学生进一步认识了圆的特征，并探索了圆的周长公式之后，本课教材结合实例引导学生认识圆的面积，让学生通过不同主题的测量活动经历圆面积计算公式的推导过程，重点突出利用已有研究图形的经验解决新问题的探究过程，从而掌握圆的面积计算公式。在探究圆面积公式的活动中，体会 “化曲为直” 的思想和方法。

对比人教版、苏教版、西师版教材发现所有版本都注重化曲为直，用转化思想将圆转化为平行四边形来推导圆的面积公式，用方格纸和圆内外正方形来估圆的面积的方法每个版本都有各自不同的处理和用力之处，其他三版教材都只注重用两种方法让学生感受面面积的估计和推导，只有北师版编排了数方格、转化和圆内方圆外方（类割圆术）三种方法，并且北师版中这三种方法都引导了学生继续想象，直至无限多的情况，从而很好地渗透了极限思想。

学情分析：

六年级的学生已经具备一定的探索、交流合作能力，好奇心、求知欲强。能够比较熟练地利用公式对已学过的平面图形进行周长和面积的计算，在本单元中学生进一步认识了圆的特征，探索了圆的周长公式，再结合已有平面图形的周长、面积公式的学习经验，能合理运用转化的数学思想，这些都为本课的学习打下坚实的基础。课前我们对班上 40 名学生进行了问卷调查，全班有 13 名学生会用圆的面积计算公式来计算，但是没有一个人知道为什么圆的面积计算公式是这样的，因此，我们认为，帮助学生厘清圆的面积计算公式的推导过程尤为重要。

教学目标：

1、结合实例认识圆的面积，经历圆面积计算公式的推导过程，掌握圆的面积计算公式。

2、通过观察、猜想、操作、验证、讨论、归纳，经历并理解圆面积计算公式的推导过程；进一步体会转化方法的价值，发展学生的逻辑思维能力和量感，体会化曲为直和极限思想。

3、在探索圆面积计算公式的过程中，养成独立思考、合作交流、反思质疑的学习习惯，会用圆的面积计算公式解决生活中的实际问题，培养应用意识。

教学重点

经历并理解圆面积计算公式的推导过程。

教学难点

进一步体会转化方法的价值，体会化曲为直和极限思想。

教学准备：

教具准备：多媒体课件

学具准备：圆纸片、剪刀、胶棒、方格纸、展示背景板、彩笔等

教学过程：

一、触发：创设情境，激趣引入

师：今天老师带来了一段关于成都夜景的小视频，想邀请大家一起来欣赏，愿意吗？

播放视频《成都的夜景真美丽》（18 秒）

师：当时我看到它的时候想的和大家还有些不一样，谁猜到我当时这么想的？

预设：

1、想到圆。

2、圆的面积是多少？

……

师：说的都对。同学们也学会用数学的眼光来看世界啦！瞧，中间的广场像一个太极八卦图，所以又被称为 “太极广场”。想知道它有多大，其实就是要求 圆的面积 ，这恰恰就是今天这节课我们要一起来研究的问题。

二、追究：探究新知

（一）回顾唤醒

师：关于 面积 ，我们是从什么图形开始研究的？

通过谈话引导学生回忆有关面积的探究过程以及探究方法经验。

师：那之前我们研究面积所用的方法还灵吗？实践出真知，灵不灵试过才知道。

先试用一个单位面积。

师：你有什么发现？

生：摆不完，有剩余……

师：还能用这种方法继续测量吗？

生：换更小的面积单位来测量。

师：那好，我们一起来试试。

（二）方法迁移，新知探究

1. 独立研习，探索新知

学习活动（一）：数方格，估测圆的面积

红袋：数方格

师：我们如果把中间包含完整面积单位的方格图上颜色，会怎样呢？请大家涂一涂。

学生独立完成涂色，教师收集作品展示

提问：观察这几幅作品，你有什么发现？

预设：1、方格越小，数出的方格越来越多了。

2、随着格子越来越小，剩余部分的越来越少了。

3、中间的形状越来越像圆了。

师：想象一下，如果方格更小呢？会怎样？

生：随着方格越来越小，涂色部分的面积就越接近圆的面积。

师：同学们能借助以前的学习经验来探索圆的面积，很棒！在研究的过程中有疑惑吗？

预设：1、尽管越来越接近，但是这样数很麻烦……

2、只能越来越接近，还是没有得到圆的面积。

3、还是不知道怎么算的啊？

师：有道理，为什么其他图形可以测量，而圆不行？

生：因为它的边是弯曲的

师：能不能把它 “化曲为直” 呢？

生：可以分割、把它转化成我们学过的图形来研究

师：我们已经研究过哪些图形的面积呢？

生：长方形、正方形、平行四边形、三角形、梯形……

2. 同伴研讨，探索解惑

学习活动（二）：转化图形，推导圆的面积公式

师：能想到这么多，老师既惊喜又佩服。你们想选择什么思路来研究呢？和组内同伴讨论一下。

组内讨论商量选择研究方法

师：为了方便大家研究，老师为大家在黄色袋子里准备了圆、剪刀等工具材料。另外同学们 发现我这儿还为大家准备了两个蓝色学习袋，这里面装的什么呢？老师先保密，有没有哪个组愿意挑战一下？

学生根据学习材料，分小组完成活动，教师巡视指导。

3. 团队研述，探索提炼

分不同方法展开小组汇报。

黄袋：转化成学过的图形

（1）A 组：转化成平行四边形（详）

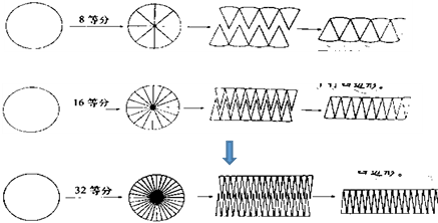
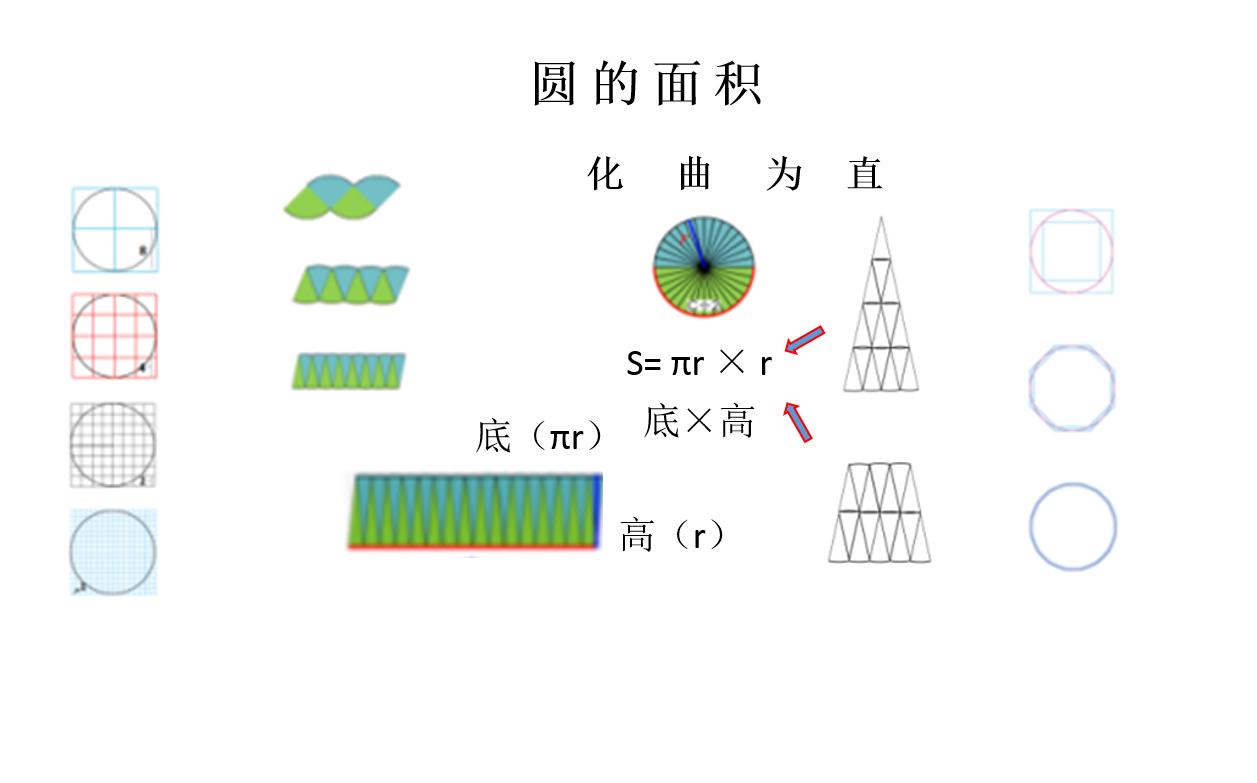
学生汇报预设：我们小组把圆转化成了近似的平行四边形。先将圆平均分成 4 份、8 份 16 份、32 份，把它拼成一个近似的平行四边形。

生 ₂：我们发现随着边数增加，平行四边形的边越来越平。随着等分的份数越来越多，拼出来的图形越接近平行四边形。虽然形状变了，但是面积没变，平行四边形的面积就是圆的面积，通过对比，我们发现平行四边形的底就是圆周长的一半，平行四边形的高就是圆的半径，

平行四边形面积 = 底 × 高

圆的面积 = 圆周长的一半 × 半径

师：这组给大家带来的信息量很大，让我们一起再来梳理一下。刚开始他们拼成的图形为什么不像？

生：边是弯的

师：随着等分的份数越来越多之后呢？

生：边越来越直了！

师：想象一下，如果就这样继续分割下去会怎样呢？让我们一起来看看。

播放视频《极限切割圆》

师：随着等分的份数越来越多，拼成的图形也越来越像平行四边形，最后变成长方形。

追问：转化成的平行四边形的底和高与原图形有什么关系？

你怎么知道平行四边形的高是圆的半径？底是圆周长的一半？

（2）师：还有没有其他想法？

B 组①：拼成近似的三角形。（略）

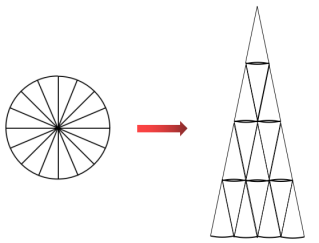
把圆形平均分成 16 份，拼成了这样一个三角形。这个三角形的面积等于圆的面积。

B 组②：拼成近似的梯形。

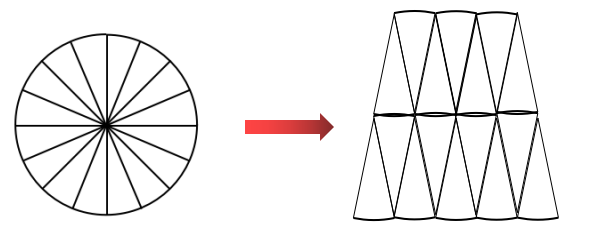
预设：我们把圆形平均分成 16 份，拼成了一个近似的梯形。

圆的面积 = 梯形的面积

师：同学们真厉害！那你们用出拼成的三角形和梯形推导出相同的圆的面积计算公式呢？课后我们继续研究、推导。

师：还有同学挑战了新方法，让我们来听听他们是怎样想的。

（3）蓝袋：割圆术等其他方法

预设：内接正多边形、外切正多边形、正方形减去四个近似的三角形等

师：哇，你们的方法太有创意了。真是未来的数学家，当初阿基米德、刘徽也是这样研究圆的。

播放视频《割圆术》

（由于时间关系，如果学生没有来得及推导其他图形与圆的面积公式之间的联系，可以布置成课后探究作业）

（三）课堂小结

师：同学们，通过这节课的学习，你有什么收获？

预设：

1、我知道了圆的面积公式是怎么推导出来的。

2、我知道了可以用数单位面积的个数、化曲为直的转化方法来研究圆的面积，推导圆的面积计算公式。

3、我知道圆就是越来越多，无限多。

……

师：刚才我们通过数方格、分割圆将圆转化为学过的基本平面图形，通过对比圆和基本平面图形直接各部分的关系，推导出了圆的面积计算公式。还在这个过程中感受了方格越小，估计出来的圆的面积越精确，分割的份数越多，拼出来的图形越接近平行四边形，这就是我们数学中非常重要的思想 —— 极限思想。同学们还利用已经学过的图形来帮助研究新图像 —— 圆。这也是数学中的重要思想 —— 化曲为直。

三、提升：迁移应用

师：现在我们来算算天府广场中间的这个太极广场到底占地面积是多少呢？

问题：天府广场中间圆形部分的半径为 75 米，那么它的面积是多大呢？

S=πr²=3.14×75²=17662.5m²

四、全课总结

板书设计