课后访谈 3：

链接：https://v.youku.com/v_show/id_XNTEzODg3ODI1Mg==.html?firsttime=3

课后访谈 2：

链接：https://v.youku.com/v_show/id_XNTEzODg3ODE4MA==.html?firsttime=4

课后访谈 1：

链接：https://v.youku.com/v_show/id_XNTEzODg3ODAyOA==.html?firsttime=7

板书设计：

终稿教学视频（百度网盘链接）：

链接：https://pan.baidu.com/s/1X4hYw7REVvLkhuFAu6xWLw

提取码：rzwp

终稿教学视频：

链接：https://v.youku.com/v_show/id_XNTEzODgzNjQwNA==.html?firsttime=6

四、深化思维 挖掘本质 --- 内化计量单位不同呈现形式的缘由

课后思考：为什么相邻长度单位、面积单位和体积单位之间的进率呈 10 倍递增？

【设计意图】课上通过多个教学活动，对于不同计量单位进行了直观呈现，已经完成 “课前量感感知体验 --- 课上量感表象建立” 的多维度衔接，希望借助课后量感的延展进一步内化知识细节，通过不同计量单位之间内在联系的探索，完成不同维度量感表象的不断深化，学生从低阶思维徘徊转向高阶思维输出，从而实现学生由浅表学习向深度学习迈进。

三、同构梳理 归纳总结 --- 完善不同计量单位关系框架

师：同学们刚才用这么多方法探究出了体积单位之间的进率，那么这节课我们学习的就是 体积单位的换算（板书）， 那到现在为止我们就学习过了长度单位、面积单位和体积单位的换算了，接下来我们进行一下梳理，它们相互之间都有着怎样的关系？

学生自由发言讨论并完成小黑板，填写表格。梳理出长度单位、面积单位和体积单位之间的关系如下：

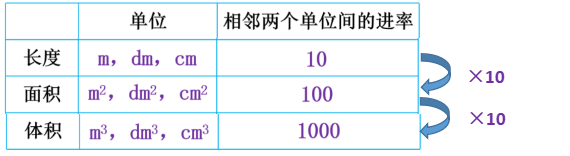
【设计意图】明确各体积单位和容积单位之间的关系，将长度、面积和体积三种不同计量单位之间的换算进行梳理，帮助学生顺利完成从一维到三维计量单位的构建。

活动二：

教师在教室前面依次摆放 3 立方分米、15 立方分米、30 立方分米、100 立方分米、500 立方分米、1 立方米等的立方体。

1. 教师按照从小到大的顺序出示立方体，学生估测每一个立方体的体积，再明确 1 立方米的立方体。

2. 将不同的物体依次放入把 1 立方米的箱子旁边进行比较。

3. 用其他立方体堆出 1 立方米大小。

探究：1 立方米里面有多少个 1 立方分米？

学生小组汇报。

生 1：将 1 立方分米正方体放入 1 立方米正方体中，发现一行可以摆 10 个，再在剩下的每一行都摆了 1 个，发现一层可以摆 10 行，又在每一层摆了 1 个，发现可以摆 10 层，那么可以摆 10×10×10=1000 个，所以 1 立方米 = 1000 立方分米。

生 2：1 米就是 10 分米，那么 1 立方米的正方体也就是棱长是 1 米的正方体，即棱长是 10 分米的正方体，由正方体体积公式得到：体积为 10×10×10=1000 立方分米。

【设计意图】此环节激励学生通过类比猜想、估测等动手操作，从三个层面对立方分米和立方米进行无痕过度：及时巩固立方分米相关知识，并将立方分米应用于生活常见的物体，建立直观量感；根据两个不同物体的体积差，感受 1 立方米和所放物体的相对大小；感受 1 立方米的大小的同时，进一步引发 1 立方米和 1 立方分米之间关系的思考。通过不断抽象化的度量方式提升量感，发展空间观念。

活动一：

教师引导学生借助已给学具进行自主探究。

1. 独立思考，确定比较方法；

2. 小组合作交流，探究 1 立方分米里到底有多少个 1 立方厘米。

学生小组汇报。

第一层次：（10 片）

利用由 100 个小正方体拼成的长方体片和由 10 个小正方体拼成的长方体条，将大正方体填满，发现所用学具相当于 1000 个 1 立方厘米小正方体的大小，所以 1 立方分米 = 1000 立方厘米。

第二层次：（3 片 + 7 个）

利用学具将大正方体填满几层，发现每一层都相当于 100 个 1 立方厘米，再用 1 立方厘米小正方体竖着摆满一竖行，发现需要摆 10 层，100×10=1000 个，所以 1 立方分米 = 1000 立方厘米。

第三层次：（1 片 + 9 个）

利用学具将大正方体铺满一层，相当于 100 个 1 立方厘米，再用 1 立方厘米小正方体竖着摆满一竖行，发现需要 10 层，100×10=1000 个，所以 1 立方分米 = 1000 立方厘米。

第四层次：（长宽高各 1 条）

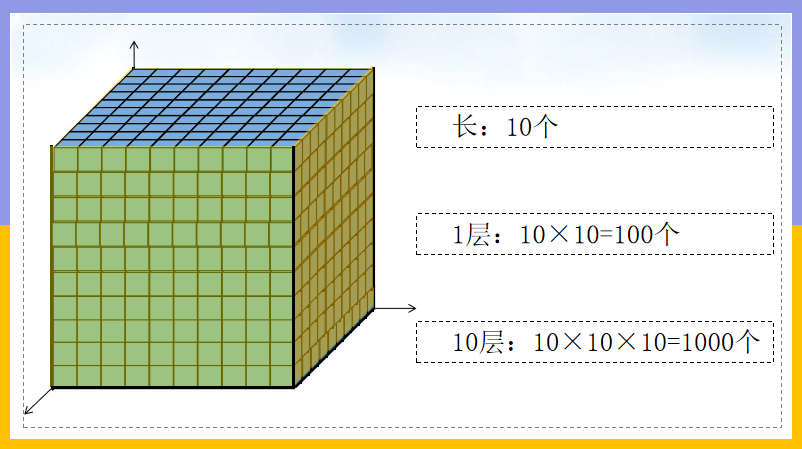
将 1 立方厘米正方体放入 1 立方分米正方体中，一行可以摆 10 个，剩下的每一行都摆了 1 个，发现一层可以摆 10 行，又在每一层摆了 1 个，发现可以摆 10 层，那么可以摆 10×10×10=1000 个，所以 1 立方分米 = 1000 立方厘米。

教师利用课件补充：一行可以放 10 块；有 10 行，需要 ×10，一层相当于 10×10=100 块；又有 10 层，需要再 ×10，一共相当于 10×10×10=1000 块。

第五层次：（算式）

1 分米就是 10 厘米，那么 1 立方分米的正方体也就是棱长是 1 分米的正方形，即棱长是 10 厘米的正方体，由正方体体积公式得到：体积为 10×10×10=1000 立方厘米。

【设计意图】在这一环节中，通过学生动手操作，帮助不同层次学生亲身感受 1 立方分米和 1 立方厘米之间的大小关系，得到 1 立方分米 = 1000 立方厘米的结论，并进一步加深对量的感知。通过动手实践，完成学生对 1 立方分米的初步认识；基于数量的不断累加，完成对 1 立方分米的深度构建。

二、活动载体 多元探究 --- 完成不同体积单位量感输入

教师出示学生熟悉的 1 立方厘米正方体若干和 1 立方分米正方体盒子学具。

师：大盒子跟巧克力盒子是一样大的，小正方体和小巧克力是一样大的，现在你能判断哪个更多吗？请同学们利用这两种学具动手试一试。

预设：

学生将一袋 1 立方厘米的小正方体全部倒入 1 立方分米的盒子里，发现没有装满，因此一大盒巧克力更多。

教师追问：把整个盒子装满需要多少块？

学生观察两种规格正方体，判断它们的大小分别是 1 立方分米和 1 立方厘米。

【教学过程】

一、实物感知 直观比较 --- 唤醒已有量感相关经验

出示动画微课情境 : 六一儿童节到了，淘气和笑笑要给班级里小朋友们买一些巧克力作为小礼物。笑笑看中了一大盒巧克力，淘气发现了一袋价格相同的袋装巧克力，里面有许许多多小巧克力。他们不知道哪种巧克力更划算，开始争论不休。一旁的奇思挠了挠头：“哪种巧克力更多呢？”

学生通过视觉感知做出初步判断，看法不一，有的认为一盒的多，有的认为一袋的多。

【设计意图】通过学生喜闻乐见的教学情境，利用实物刺激，引发学生思考，引导学生通过对体积 “量感” 的生活感知，即运用 “已有量感” 的基本经验，对情境中的两个元素进行初步判断。

微课链接：https://pan.baidu.com/s/1g12nLliYQb3oi1CWD81XFQ

提取码：08jp

【教学目标】

1. 结合实践活动，理解体积单位之间的进率，会进行体积单位之间的换算。

2. 在观察、操作中培养学生空间观念，同时建立并发展学生的 “量感”。

3. 探究过程中，积累相关活动经验；渗透归纳和类比的数学思想。

【教学重点、难点】

重点：观察、操作中会进行体积单位之间的换算。

难点：通过度量等方式推导体积单位间的进率和建立相应的空间观念。

【教学准备】

教具准备：1 立方米正方体框架、1 立方米正方体箱子、500 立方分米立方体、100 立方分米立方体、30 立方分米立方体、3 立方分米正方体、10 立方分米长方体木条 10 根，1 立方分米正方体 9 个、正方体小凳子若干。

学具准备：每组一块小黑板、1 立方分米正方体 1 个、100 立方厘米长方体片若干、10 立方厘米长方体条若干、1 立方厘米正方体若干。

【学情分析】

五年级的学生好奇心强，求知欲旺盛，并且已经具备一定的自主探究能力。虽然思维能力有所提升，但还是以形象思维为主，在逐渐向抽象思维过渡的时期。对于 “物体大小” 已经积累了丰富的生活经验，所以，课程设计一定要基于学生的生活经验和认知起点。体积单位是继长度和面积单位之后，再次学习计量单位。学生已经初步具备 “量感” 积累的相关基础，但对于各个单位间的换算不甚清晰，谈及这三者的联系及区别更是愈发混沌，介于时而清晰，时而糊涂的尴尬境地。总体来看，学生们学习本课的基础认知广泛，但学透本课的障碍也同时存在。所以，设计好本课内容，打通各个计量单位间的壁垒尤为重要。

教学设计终稿：

【教材分析】

1. 北师版教材内容分析：

本课是北师大版五年级下册第四单元第六课时。本单元是在一年级学习过 “认识长方体、正方体、圆柱、球” 以及五年级下册第二单元 “长方体（正方体）的认识与表面积” 的基础之上进行学习的，这一单元的内容也为后续学习 “认识圆柱和圆锥”、“圆柱的表面积和体积”、“圆锥的体积” 等做铺垫。而 “体积单位的换算” 一课是在学习完 “体积单位” 和 “长方体体积” 之后进行的，在前两节课的基础之上将内容进行了进一步的加深，同时将 “长方体体积” 的知识融会贯通于本课。《体积单位的换算》一课在北师版教材中共安排了三个问题串。第一个问题串是通过两种不同的方法来解决问题的，即：利用长度单位的换算和求长方体的体积以及利用拼摆图形的方法，引导学生通过度量找到立方厘米和立方分米这两个相邻体积单位之间的进率。第二个问题串可以通过类比第一个问题串的条件和结论进行合理猜想，也可以通过上述的两种方法进行计算和拼摆图形得出结论，提高学生举一反三的能力。第三个问题串帮助学生形成一定的知识体系。三个问题串紧密相连，让学生充分经历体积单位换算的过程，体会各个常见体积单位有多大，以及它们之间的大小关系。

2. 与其他版本教材对比：

同一知识内容在人教版教材中的设置却有所不同，第一环节，与北师大版教材恰恰相反，拼摆与切割，通过两种不同的角度解决同一问题。第二环节，通过类比上述方法推算出 1 立方米等于多少立方分米。第三环节，对长度单位、面积单位以及体积单位换算的归纳与总结。

3. 归纳不同版本共通点：

两个版本都是用了很大篇幅和时间进行学生动手操作的实践，无论是拼摆法还是切割法，都充分体现了度量的必要性。这一点给我们很大的启迪：

①基于学生动手实践完成知识学习；

②借助几何直观，化抽象为具体展开教学。